Recibido: 24 de octubre de 2013.
Aceptado: 21 de febrero de 2014

 

Introducción

En la teoría económica predominantemente aceptada en nuestros días, las remuneraciones al trabajo y, en general, el pago a los factores de la producción, están relacionados con su productividad. Desde que Wicksell la formalizó con claridad, bajo condiciones típicas de la economía neoclásica (Samuelson, 1979), esta relación (ya propuesta con anterioridad por otros economistas contemporáneos de él) se ha establecido como determinante de la distribución del ingreso. A partir de esta proposición, la teoría del mercado de trabajo ha evolucionado en gran medida hacia la de la dualidad de los mercados de este factor de la producción, de forma notable después del estudio pionero de Lewis (1954), en el que expuso lo que se ha convertido en el modelo dual clásico de crecimiento, donde el tema fundamental fue la asignación del trabajo entre dos sectores.

Una de las aportaciones fundamentales de Lewis fue, quizá, el postulado de que en uno de los sectores, el agrícola (o el informal), la remuneración al trabajo no estaba vinculada a la productividad sino, más bien, a una forma de institucionalidad. En este aspecto (y otros), su modelo se alejó de los postulados neoclásicos y ha dado pie para formular modelos teóricos que explican fenómenos que se observan en las economías contemporáneas. Stiglitz (1974), por ejemplo, propuso uno para dar cuenta de la persistencia de diferenciales en las remuneraciones de trabajadores de características similares, fenómeno para el que la teoría del equilibrio de mercado es insuficiente.

La presencia de remuneraciones determinadas por criterios distintos a los del mercado, en un sentido convencional, ha conducido a la formulación de la hipótesis de los salarios de eficiencia, es decir, aquellos que difieren de los de equilibrio (determinados por la oferta y la demanda de trabajo), que se establecen con otros criterios (incentivar la productividad y reducir la rotación) y que ayudan a explicar fenómenos como el nivel de desempleo y la discriminación (Bulow y Summers, 1986).

En esta investigación se toman en cuenta factores que, por su relación directa con la productividad, inciden en las remuneraciones, notablemente el capital humano. Uno de los pasos más importantes en esta materia se vincula a Gary Becker con su obra clásica Human Capital de 1964, en la que analiza la tasa de retorno a la escolaridad. Desde entonces, el análisis en cuestión se ha abordado con mayor frecuencia, añadiendo otros factores, incluidos algunos que tratan de especificar con más precisión el nivel de educación, como la llamada Teoría de la señalización (Arrow, 1973; Spence, 1973; Taubman y Wales, 1973), o los de autores que indican que una estimación técnicamente correcta del retorno debe considerar los costos de oportunidad y financieros en que incurren los individuos que deciden alcanzar niveles educativos más altos (Rojas et al., 2000; Harberger y Guillermo, 2012); además de la educación como indicador del capital humano, se han considerado otros condicionantes del nivel de ingreso de carácter estructural. La relevancia del análisis de los determinantes de las remuneraciones deriva de las conclusiones que éste puede arrojar, en relación con el diseño y ejecución de políticas públicas orientadas a incidir en el monto y distribución del ingreso.

El objetivo del estudio es realizar un análisis de los principales determinantes de las remuneraciones¹ de los trabajadores de la industria² en México, con énfasis en la inclusión conjunta de variables de oferta y demanda laboral, la estimación puntual del retorno a la educación, así como el efecto de la prima salarial por sindicalización.

La mayor parte de la literatura sobre el tema de esta investigación pone énfasis en los rasgos que caracterizan la oferta de trabajo —como la calidad del capital humano— para explicar el nivel de las remuneraciones. Si bien éstos pueden ser los más relevantes, es de esperarse que las características de la demanda tengan una influencia significativa, ya que son condicionantes de la productividad, así como otras que pueden estar relacionadas con aspectos que pueden denominarse institucionales, como la forma de organización de los trabajadores y la discriminación por sexo.

En este contexto, factores como el tipo de industria (Castelar y Ramos, 1994), los estratos ocupacionales (Muñoz, 2004) y la discriminación por sexo en sectores específicos (Brown y Domínguez, 2007) han sido agregados al análisis de los diferenciales en los salarios o el conjunto de las remuneraciones. Otros autores también han documentado la importancia de la tasa de sindicalización como factor que ha contribuido a cerrar la brecha entre los ingresos percibidos por los trabajadores, según estén o no afiliados a un sindicato; así lo han referido Fairris y Levine (2004), Esquinca y Melgoza (2006) y Zepeda (2009).

En el siguiente apartado se hace referencia a las fuentes de los datos de la presente investigación; enseguida, se explica el método propuesto y los supuestos empleados en las estimaciones que se detallan en la sección de resultados y, por último, a manera de conclusión, se exponen los principales hallazgos del trabajo y se realizan recomendaciones de políticas públicas.

1. Fuentes de información

La doble naturaleza de los determinantes de las remuneraciones al trabajo dificulta la medición de la influencia que tienen, porque no es frecuente que se disponga, al mismo tiempo, de información sobre las características personales y las estructurales. Las fuentes de información para este tipo de estudios suelen ser encuestas de ingreso-gasto familiar, las cuales usan como informante al individuo y obtienen directamente datos sobre él y los miembros de su hogar, y de manera limitada acerca de las características de su ocupación y el establecimiento donde la desempeña, lo que restringe en alguna medida el alcance del análisis.

Las investigaciones recientes sobre el tema en México emplean, por lo general, datos de la Encuesta Nacional de Ingresos y Gastos de los Hogares (ENIGH), como en Panagides y Patrinos (1994), Zamudio (1995), Rojas et al. (2000), Barceinas (2003), Popli (2005) y Esquinca y Melgoza (2006). Otra fuente ha sido la Encuesta Nacional de Empleo, Salarios, Tecnología y Capacitación en el Sector Manufacturero (ENESTyC), como en Fairris (2007). Además, autores como Villarreal (2010), Varela y Retamoza (2011) y Harberger y Guillermo (2012) han empleado la Encuesta Nacional de Ocupación y Empleo (ENOE) y otros, como López-Acevedo (2004), Rodríguez-Oreggia (2005) y Urciaga y Almendarez (2006) han utilizado a su predecesora, la Encuesta Nacional de Empleo Urbano (ENEU), todas elaboradas por el Instituto Nacional de Estadística y Geografía (INEGI).

Para los fines del presente trabajo, se ha tomado en consideración la ENOE, la cual recopila datos cada trimestre, desde el 2005, en una muestra de alrededor de 120 mil viviendas. Su diseño muestral es probabilístico, bietápico, estratificado y por conglomerado,³ y cuenta con datos sobre las características sociodemográficas, de ocupación y empleo de la población de 12 años de edad y más. Es la herramienta más completa de que se dispone en México para el análisis del entorno laboral. Más aún, el INEGI proporciona (para los primeros trimestres de cada año del 2009 en adelante) los microdatos que provienen del cuestionario ampliado de ocupación y empleo, con información detallada sobre las características del contexto laboral de los individuos.

Esta investigación se basa en los resultados de la ENOE del primer trimestre del 2013, de la que se obtuvieron 29 163 observaciones para los trabajadores remunerados y subordinados del sector industrial, en tanto que, como fuente especializada en el ámbito laboral, ha permitido aprovechar la disponibilidad de información sobre variables de oferta y demanda laboral para las estimaciones del presente trabajo.

2. Método general de estimación

Siguiendo la estructura básica ampliamente utilizada desde el trabajo pionero de Mincer (1974), la ecuación inicial a estimar es:

(1)

donde log w_i representa el logaritmo de la remuneración recibida por el individuo i, explicado por k variables X que, de acuerdo con el trabajo de Mincer (1974), serían el nivel educativo y la experiencia laboral (y su cuadrado) del individuo i.

De acuerdo con Lemieux (2006), esta especificación sigue siendo válida, aunque se requeriría emplear una función de cuarto grado de la experiencia, ya que se pueden subestimar los efectos de esta variable sobre trabajadores jóvenes, así como adicionar un término cuadrático de los años de escolaridad para tomar en cuenta la relación convexa con las remuneraciones. Respecto al primer caso, se realizará el ejercicio para validar su aplicación a la situación mexicana; en cuanto al segundo, en el siguiente apartado se detalla la estimación del efecto del nivel educativo.

Además, Lemieux (2006) comenta que es necesario controlar por efectos de cohorte, pues se comprueba que, por lo menos en Estados Unidos de América (EE.UU.), han existido cambios en la estructura de los diferenciales entre oferta y demanda de trabajadores por nivel educativo a través del tiempo. Antes de 1980, la proporción de la población joven con educación superior en México era menor a 1% y el crecimiento económico era relativamente alto, por lo que la probabilidad de emplearse para este sector era muy alta. En las décadas siguientes, las tasas de crecimiento del producto interno bruto (PIB) se redujeron de manera importante al mismo tiempo que se incrementó de forma significativa el porcentaje de la población de 15 a 29 años con educación media superior y también —aunque a una tasa menor— el correspondiente a las personas con educación superior, por lo que resulta probable que la demanda laboral no fuera suficiente para absorber a este grupo con mayor educación (ver gráfica). De aquí que en nuestras estimaciones se utilizarán variables dummy por rangos de edad para controlar estas posibles variaciones.

De manera adicional, de acuerdo con la Teoría de señalización, además de representar una forma de capital, el papel de la educación es resolver un proceso de información asimétrica (Duarte, 2012) en el que los demandantes de trabajo utilizan los títulos educativos obtenidos como parámetro de eficiencia, ante la ausencia de información sobre su productividad. Para modelar esta teoría, se estimará una ecuación adicional, en la cual se emplean variables que identifican los estudios completados por los individuos, como alternativa a la variable de años de escolaridad.

En investigaciones para México, Rojas et al. (2000) y Harberger y Guillermo (2012) agregan a los modelos derivados de la ecuación de Mincer los costos asociados con la adquisición de más años de escolaridad, sobre todo el salario que percibiría cada individuo si decidiera entrar al mercado laboral con el nivel educativo alcanzado, en lugar de continuar con sus estudios. La incorporación de este costo de oportunidad tiende a reducir la ahora denominada tasa interna de retorno a la educación (Rojas et al., 2000). En el presente estudio no se incorporan estas consideraciones, ya que el modelo planteado permite obtener la dirección en que la educación afecta los ingresos esperados por los individuos.

El modelo se completa con la adición de variables sociodemográficas (sexo y estado conyugal) y laborales (ocupación y tipo de contrato). Se toman en cuenta, además, variables del lugar de trabajo, como el tamaño de la empresa, condición de formalidad de la unidad económica y productividad⁵ de la rama de actividad de la empresa. La estimación de la prima sindical se considera más adelante.

2.1 Endogeneidad del nivel de escolaridad

En la literatura se menciona que hay una correlación entre las características de los individuos —por ejemplo su habilidad— y las decisiones sobre la adquisición de un mayor capital humano (Kling, 2000; Arias, Hallocky Sosa, 2001; Leigh y Ryan, 2008), lo que sugiere la necesidad de aplicar un método estadístico idóneo para controlar este sesgo por endogeneidad. Para ello, se han utilizado variables instrumentales (VI) que permiten obtener un estimador insesgado y consistente del retorno a la educación.⁶

Existe una variedad de instrumentos para llevar a cabo las estimaciones; por lo general tienen que ver con características familiares, como la educación o clase social de los padres, el número de hermanos (Sarimaña, 2002; Blundell, Dearden y Sianesi, 2005), la proximidad a la escuela (Kling, 2000), el orden de nacimiento (Booth, Coles y Gong, 2006) y el mes de nacimiento (Angrist y Krueger, 1991; Webbink y van Wassenberg, 2004; y Leigh y Ryan, 2008).

Por medio de la ENOE no es posible asociar las características familiares para todos los individuos,^7> sin embargo, el mes de nacimiento puede ser obtenido de su base de datos, variable que es poco probable que esté correlacionada con otros atributos personales —por ejemplo, el ingreso— distintos a la edad en que los individuos entran a la escuela⁸ (Angrist y Krueger, 1991) y que, por lo tanto, se puede considerar como una fuente de variación exógena a la relación que guardan los años de escolaridad alcanzados y el ingreso.

Leigh y Ryan (2008) argumentan que pueden existir diferencias en el nivel de escolaridad de estudiantes con distintos meses de nacimiento, relacionados con las fechas señaladas como límite para poder entrar a la escuela primaria; por ejemplo, si un individuo X nació el día límite de ingreso a la escuela y otro (Y) un día después, X entraría a la escuela un año antes que Y, ceteris paribus, a pesar de haber nacido con un día de diferencia. Lo anterior afecta la cantidad de educación recibida en relación con los años vividos y quizá, también, la calidad de la misma, según sea el individuo el más joven o más viejo del grupo escolar.

Entonces, la ecuación a estimar en la primera etapa sería:

(2)

donde Mes_i toma los valores 4, 3, 2, 1, -1, -2, -3, -4 según el número de meses transcurridos entre el nacimiento del individuo i y la fecha límite de ingreso. Los valores negativos se asignan a los estudiantes nacidos en los meses posteriores a la fecha límite de ingreso, bajo el supuesto de que, al haber comenzado sus estudios a mayor edad, aumenta la probabilidad de que acumulen menos años de escolaridad, al existir mayores presiones para ingresar al mercado laboral.

Adicionalmente, las fechas de ingreso y sus requisitos (entre otros aspectos) han variado de unas partes del país a otras, por lo que es necesario controlar dichos efectos. Al tomar esto en cuenta, la ecuación (2) puede estimarse como sigue:

(3)

donde Año_i representa el año de nacimiento del individuo i, en interacción con su mes de nacimiento⁹ Mes_i . A pesar de que antes del 2006 la fecha límite de nacimiento para matricular a un niño en primero de primaria era el 31 de agosto, se hizo una estimación adicional de las ecuaciones (2) y (3) con el 31 de diciembre, ya que las autoridades escolares observaban cierta flexibilidad respecto a la fecha de nacimiento para permitir la inscripción de niños nacidos en fechas posteriores. De hecho, a partir del 2006, el límite es el 31 de diciembre.

Cabe destacar que en 1966 se unificaron los calendarios escolares en México pues antes existían dos fechas diferentes para el inicio del ciclo escolar. Así, una estimación alternativa se realizará para una submuestra j tal que n_j ⊂ n_i y Año_j > 1965 ∀ j.

2.2 Prima salarial por sindicalización (PSS)

Estudios previos que estiman la PSS han adoptado diversos métodos, según sus objetivos particulares; por ejemplo, Bratsberg y Ragan (2002) estimaron ecuaciones de tipo minceriano mediante mínimos cuadrados ordinarios para calcular la PSS por industria, en EE.UU., en el periodo 1971-1999. Schmitt (2008) estima regresiones por cuantiles (quantile regression) para probar que la PSS es mayor en los percentiles más bajos. Varios autores señalan la necesidad de controlar el proceso endógeno que representa la decisión de entrar o no a un sindicato (Bryson, 2002; Blanchflower y Bryson, 2004; Barragán, 2006); para ello, utilizan el pareo por puntajes de propensión (PSM, por sus siglas en inglés, propensity score matching) como método de corrección, por el sesgo de selección que se genera.

En este trabajo se ha usado el PSM mediante pareo por el vecino más cercano (NNM, por sus siglas en inglés, nearest neighbor matching), el cual consiste en emparejar unidades tratadas (sindicalizados) y de control (no sindicalizados), emparejando aquellas de control con puntaje de propensión más cercano, para cada unidad tratada (Barragán, 2006). El método tiene la desventaja de que puede omitir información relevante en términos comparativos sobre unidades de control con puntajes cercanos a individuos tratados. Para incrementar la robustez de los resultados, se mostrarán estimaciones del NNM con 1 y 5 unidades de comparación; también, del pareo Radius, método que permite emparejar al grupo de unidades de control más cercanas dentro de cierto rango (Caliper), además del pareo Kernel, que emplea información de la totalidad del grupo sin tratamiento como unidades de comparación, otorgando mayor peso a aquéllas con puntajes más cercanos a los estimados para las unidades tratadas.

Por otro lado, Blanchflower y Bryson (2004) intentaron determinar si la existencia de una mayor proporción de trabajadores sindicalizados en las empresas incrementa el poder de negociación salarial y, por consiguiente, el diferencial salarial. Como alternativa, en el presente trabajo se emplean el tamaño de la empresa y la productividad de la industria, lo cual puede reflejar que las personas sindicalizadas trabajan en empresas de mayor tamaño y alta productividad, en las que los salarios tienden a ser mayores.

En el apéndice se encuentran los cuadros con los resultados a los que se hace referencia en la siguiente sección,¹⁰ así como la descripción de las variables utilizadas.

3. Resultados

3.1 Resultados generales del modelo minceriano

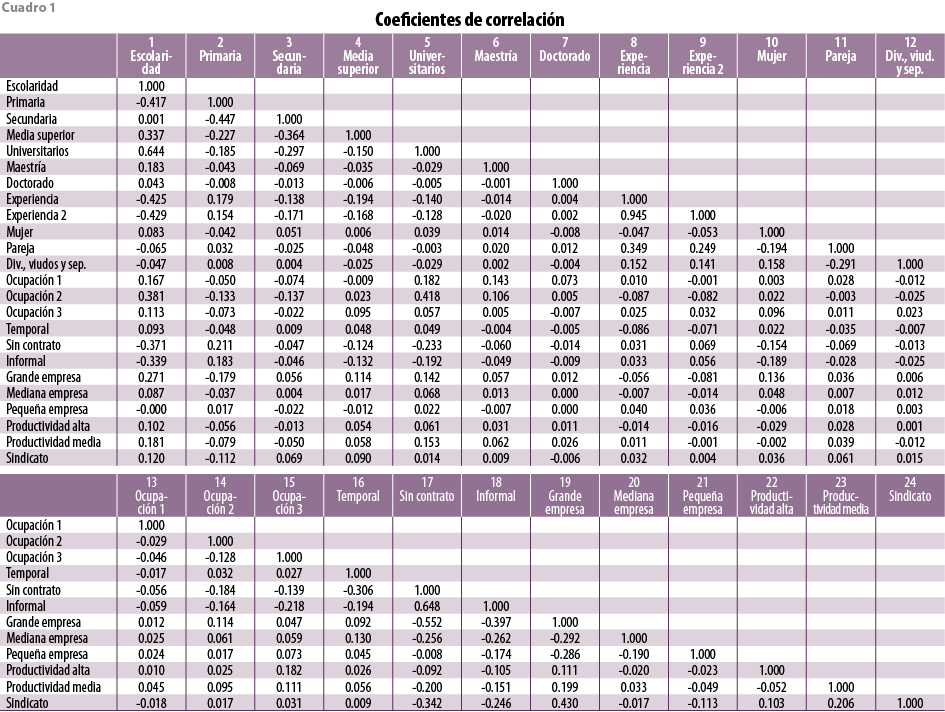
Antes de proceder a realizar las estimaciones, se revisó la correlación existente entre las variables seleccionadas de la ENOE (ver cuadro 1 del apéndice). De dicho análisis destaca que hay niveles de correlación de alrededor de 40% entre la escolaridad, por una parte, con las ocupaciones tipo 2 (profesionales, técnicos y trabajadores del arte) y trabajadores sin contrato escrito, por otra, al igual que entre la variable que mide si los individuos tienen nivel universitario concluido y el tipo de ocupación 2, y entre las variables de tamaño de establecimiento grande e informalidad. Respecto al tipo de ocupación 2, se decidió considerarla en las distintas ecuaciones ya que, como señalan Harberger y Guillermo (2012), las variables de categoría ocupacional funcionan como proxy a la habilidad de los individuos. En los otros casos, se omitirán las variables dummy de trabajadores sin contrato e informalidad cuando coincidan con las variables mencionadas con anterioridad, que están muy correlacionadas con éstas.

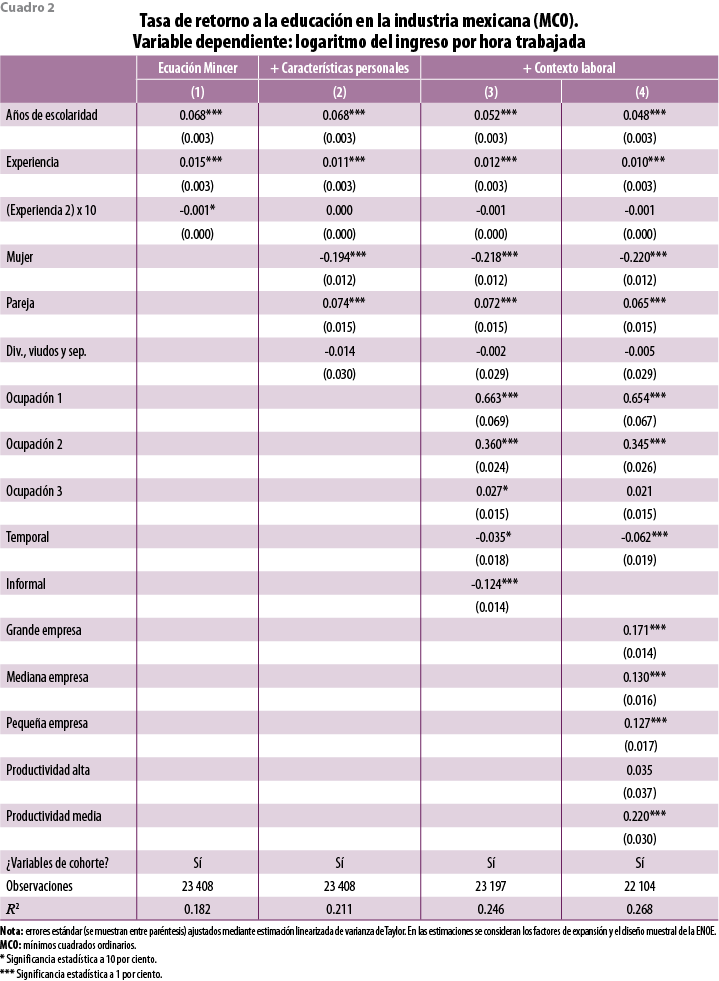
En el cuadro 2 del apéndice se muestran los resultados de las primeras estimaciones por mínimos cuadrados ordinarios. La columna 1 presenta los coeficientes de la ecuación minceriana clásica; en la 2 se agregan variables personales y en las 3 y 4 se añaden las del contexto laboral.

El primer resultado refleja un retorno a la educación en la industria mexicana de 6.8% (ver cuadro 2 del apéndice), el cual permanece robusto en las distintas especificaciones. Al agregar la variable de escolaridad al modelo completo (cuadro 2, columna 4, del apéndice) se incrementa 12.6% el ajuste del modelo, lo que hace a la variable de educación la de mayor poder explicativo.

Estudios previos para el caso de México que hacen uso de ecuaciones del tipo minceriano y datos de encuestas de ocupación y empleo (López-Acevedo, 2004; Rodríguez-Oreggia, 2005; Urciaga y Almendarez, 2006; Villarreal, 2010) han encontrado retornos promedio de alrededor de 10% para los años comprendidos entre 1987 y el 2009, por lo que nuestros resultados indican que las retribuciones a la educación han tendido a reducirse. Con base en datos de la ENOE, Villarreal (2010) explica que, a partir del 2000, los rendimientos a la educación han disminuido, en particular para los trabajadores menos calificados, ante el incremento en la demanda por trabajadores más educados.

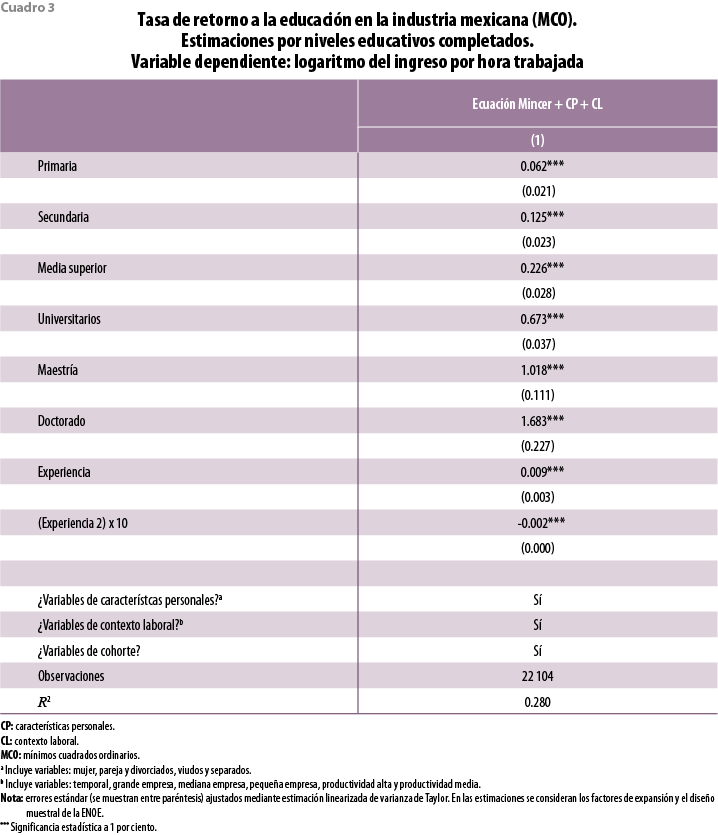
Los resultados encontrados implican que el retorno a la educación es lineal, es decir, que cada año de escolaridad adquirido representa un incremento de 6.8% en el ingreso, sin importar el grado de escolaridad alcanzado. Empleando datos por niveles completados por los trabajadores subordinados y remunerados en la industria mexicana, se encontró que si un trabajador cuenta con estudios de doctorado y maestría concluidos, su ingreso es, en promedio, 168.3 y 101.8% mayor, respectivamente, al de otro con primaria inconclusa o sin estudios, mientras que el incremento para trabajadores con nivel de educación universitario, media superior, secundaria y primaria es de 67.3, 22.6, 12.5 y 6.2%, en ese orden (ver cuadro 3 del apéndice). Siguiendo a Ordaz (2007), con los coeficientes del cuadro 3 del apéndice se calcula que el retorno a la educación en los niveles de doctorado y maestría sería, en promedio, 22.2 y 17.2% por año adicional de estudios, respectivamente. El rendimiento para trabajadores con estudios universitarios concluidos es de 8.9%, mientras que para el resto de los niveles disminuye en forma considerable; en media superior, secundaria y primaria, el retorno por grado aprobado es de 3.4, 2.1 y 1%, en ese orden.¹² Aun sin considerar los costos de oportunidad, los incentivos para continuar estudiando hasta el nivel medio superior son bajos. En particular, Rojas et al. (2000) encuentran que los estímulos económicos para concluir los estudios de secundaria en México son muy bajos, la tasa interna de retorno (considerando costos de oportunidad) es apenas de 4.4% por completar este nivel,¹³ muy similar al 4.2 estimado por Harberger y Guillermo (2012).

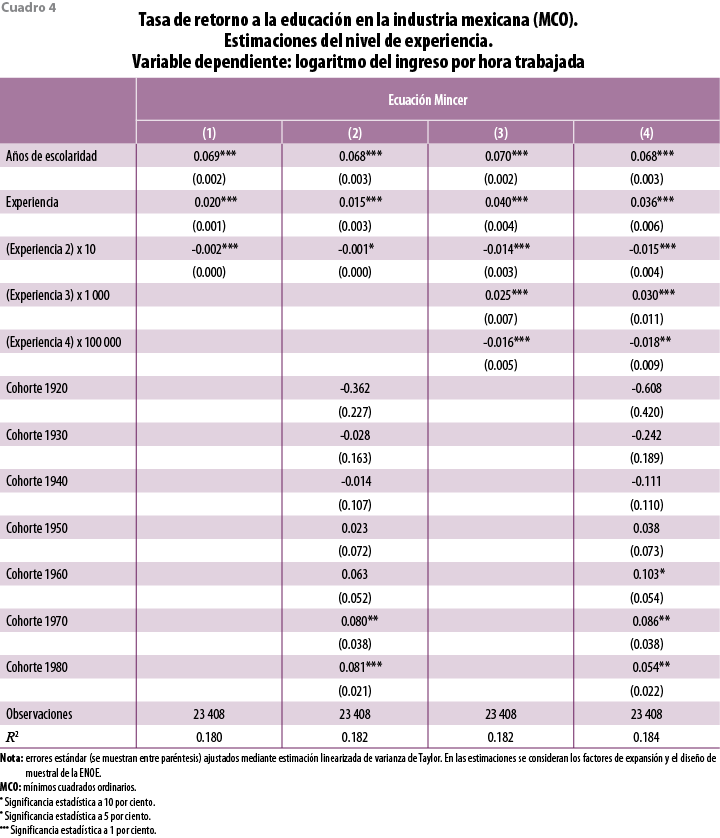
Las estimaciones para el nivel de experiencia en el cuadro 2 muestran que el ingreso apenas se incrementa 1.5% por cada año adicional de experiencia, y que se reduce de forma ligera conforme se acumulan más años de trabajo; sin embargo, incorporando dicha variable con términos que comprenden hasta la cuarta potencia (cuadro 4, columna 3, del apéndice), el efecto inicial es de 4% por año de experiencia. Además, se comprueba que existen cambios de pendiente estadísticamente significativos en esta variable, por lo que es pertinente incorporar estos términos si se busca estimar una ecuación tradicional minceriana. En términos comparativos, el efecto de la experiencia es similar al encontrado para la industria manufacturera estadounidense, donde, por cada año de experiencia, el salario se incrementa 5.3% (Bayard y Troske, 1999) y se observan, además, los mismos cambios de pendiente que en nuestras estimaciones.

Se encontró, asimismo, que una persona con pareja tiene un salario por hora trabajada 7.4% mayor que una soltera; el diferencial correspondiente a individuos divorciados, viudos y separados no es estadísticamente distinto de cero. El ingreso percibido por las mujeres en la industria es, en promedio, 19.4% inferior al de los hombres. En el contexto particular de la industria maquiladora, Brown y Domínguez (2007) encontraron que sólo puede explicarse entre 38.1 y 41.2% de la brecha salarial existente entre ambos sexos por medio de variables como la educación, experiencia, capacitación, ocupación y el tamaño de la empresa, sugiriendo la presencia de formas de discriminación que afectan el ingreso de las mujeres.

Respecto a los grupos ocupacionales, se estimó que los funcionarios y directivos ganan, en promedio, 66.3% más que los trabajadores menos calificados, mientras que el diferencial respecto a estos últimos, correspondiente a profesionistas y técnicos, es 36% superior; y el de oficinistas, comerciantes y operadores, 2.7% en términos de ingreso por hora trabajada.

Por otra parte, las estimaciones en la columna 3 del cuadro 2 del apéndice revelan que el ingreso es 12.4% inferior cuando se trabaja en el sector informal, coeficiente estadísticamente significativo. Cabe señalar que en este trabajo no se consideró el proceso de autoselección entre los sectores formal e informal. Al estimar efectos condicionales por tratamiento, Moreno (2007) encontró que un trabajador (hombre) del sector formal, en 2003, reduciría su ingreso 11.7% si se moviera a la informalidad, en tanto que si hiciera el movimiento inverso, su ingreso aumentaría 2.6 por ciento.

Si un individuo labora en una empresa grande, el salario por hora trabajada es 17.1% superior al de los que laboran en una microempresa, lo cual sugiere la existencia de una prima por trabajar en este tipo de establecimientos; el efecto se reduce a 13% en empresas medianas y 12.7% en pequeñas (cuadro 2, columna 4, del apéndice). Bayard y Troske (1999) estiman la prima salarial por tamaño de empresa en 14% en la industria de EE.UU. y concluyen que dicha prima se presenta en establecimientos de mayor tamaño debido, sobre todo, a que tienen una mayor capacidad de absorción de trabajadores más productivos.

El ingreso por hora trabajada de una persona ocupada, en promedio, en una industria de alta productividad es 3.5% superior al de una ocupada en ramas de actividad de baja productividad, aunque el resultado no es significativo estadísticamente; sin embargo, las estimaciones muestran que el ingreso por hora trabajada es 22% superior en las industrias de productividad media respecto a industrias de baja productividad. Esto puede obedecer al nivel de agregación de los datos utilizados, donde la productividad se estima a nivel de rama de actividad.

3.2 Retorno a la educación por variables instrumentales

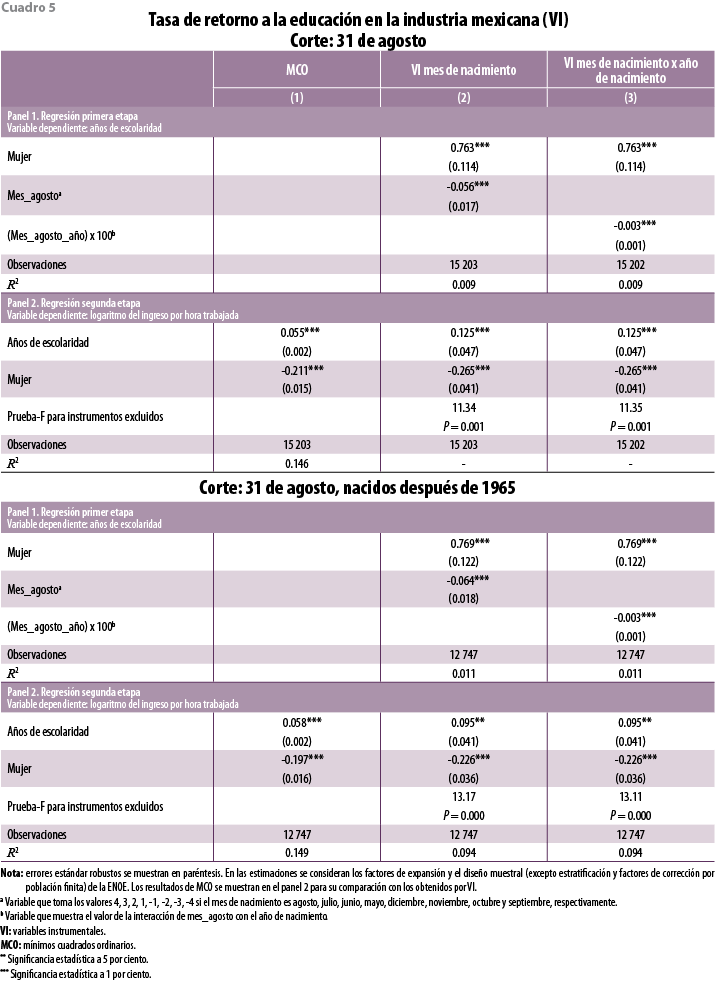
Al intentar aproximar el retorno a la educación por VI, utilizando el 31 de agosto como fecha límite para ser matriculado en nivel primaria, se encontró que el ingreso por hora trabajada aumenta, en promedio, 12.5%; esto es, 127.3% más alto que el estimado por mínimos cuadrados ordinarios (cuadro 5, panel 2, del apéndice), resultado estadísticamente robusto.

Los cálculos en la regresión de la primer etapa que estima el efecto del mes de nacimiento sobre la escolaridad (cuadro 5, panel 1, del apéndice) revelan que el nacer con posterioridad a la fecha límite de matriculación —es decir, ser relativamente más viejo que los compañeros de clase— tiene un efecto positivo sobre la adquisición de más años de estudio; por ejemplo, si un individuo nace en septiembre de un año dado, el nivel de escolaridad aumenta, en promedio, 0.3 años. Cabe destacar que el modelo de la primer etapa explica sólo 0.9% de las variaciones en los años de escolaridad.

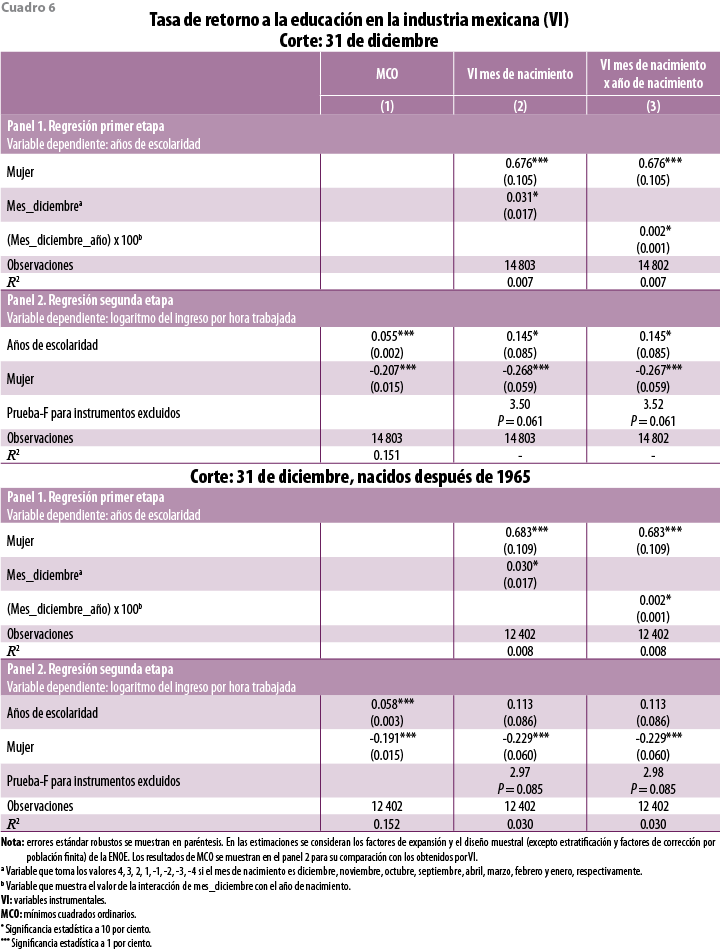
Una vez empleado el 31 de diciembre como fecha de referencia, se estima un retorno a la educación promedio de 14.5% por año de escolaridad (cuadro 6, panel 2, del apéndice), aunque el coeficiente es sólo marginalmente significativo. Se puede observar, de manera adicional (de acuerdo con el valor de la prueba F), que pueden existir instrumentos excluidos en este caso.

Respecto a los cálculos con la submuestra de individuos nacidos cuando se unificaron las fechas de inicio escolar en el país, muestran que el incremento en el ingreso laboral por año adicional de educación en la industria con fecha de corte 31 de agosto es, en promedio, 9.5%, coeficiente 63.8% más alto que el estimado por mínimos cuadrados ordinarios (continuación del cuadro 5, panel 2, del apéndice), resultado estadísticamente robusto. Por un lado, este resultado puede considerarse una mejor aproximación, ya que el instrumento utilizado refleja mejor la respuesta de los individuos al contar con un calendario escolar uniforme entre regiones; de hecho, el poder explicativo del modelo se incrementa de forma ligera, pues pasa a 1.1 por ciento. También, la baja en el coeficiente puede ser consecuencia de utilizar trabajadores de cohortes más recientes (1970 y 1980) que, según el cuadro 4 del apéndice, hablando en términos estadísticos, muestran patrones de generación de ingreso significativamente distintos a los de trabajadores de otras cohortes.

A la luz de estos hallazgos, el retorno por cada año adicional de estudio en la industria mexicana es superior al calculado por mínimos cuadrados (entre 63.8 y 127.3%), lo cual indicaría que este último método tiende a subestimar el efecto de la educación sobre el ingreso. Tanto Angrist y Krueger (1991) como Staiger y Stock (1997) utilizan el trimestre de nacimiento (en interacción con otras variables, como el año y el estado de nacimiento) como variable instrumental, y encuentran que las estimaciones por VI son, en promedio, 30 y 62% mayores que las predichas por mínimos cuadrados ordinarios, respectivamente. En un análisis sobre diversos estudios que estiman el retorno a la educación, Card (2001) encuentra que este diferencial es del orden de 20% o mayor.

Ya que los modelos tradicionales incurren en sesgos por la omisión del efecto de la habilidad de los individuos, podría esperarse que el estimador por mínimos cuadrados ordinarios tendería a sobrestimar el efecto real de la educación sobre las remuneraciones, tal es el caso de Leigh y Ryan (2008). En una primera explicación, Card (2001) comenta que la subestimación del coeficiente de mínimos cuadrados ordinarios del retorno a la educación puede ser atribuida a errores de medición. El mismo autor apunta a que éstos explican sólo 10% de las diferencias entre las estimaciones de mínimos cuadrados ordinarios y VI, por lo cual es poco probable que la amplia evidencia que encuentra una diferencia positiva entre los coeficientes estimados por ambos métodos sea resultado de errores de medición. Una segunda explicación está en que el sesgo al alza es aún mayor en los coeficientes de VI, comparados con mínimos cuadrados, debido a diferencias no observables entre las características de los grupos de tratamiento y control implícitos en las especificaciones por variables instrumentales.¹⁵

3.3 PSS

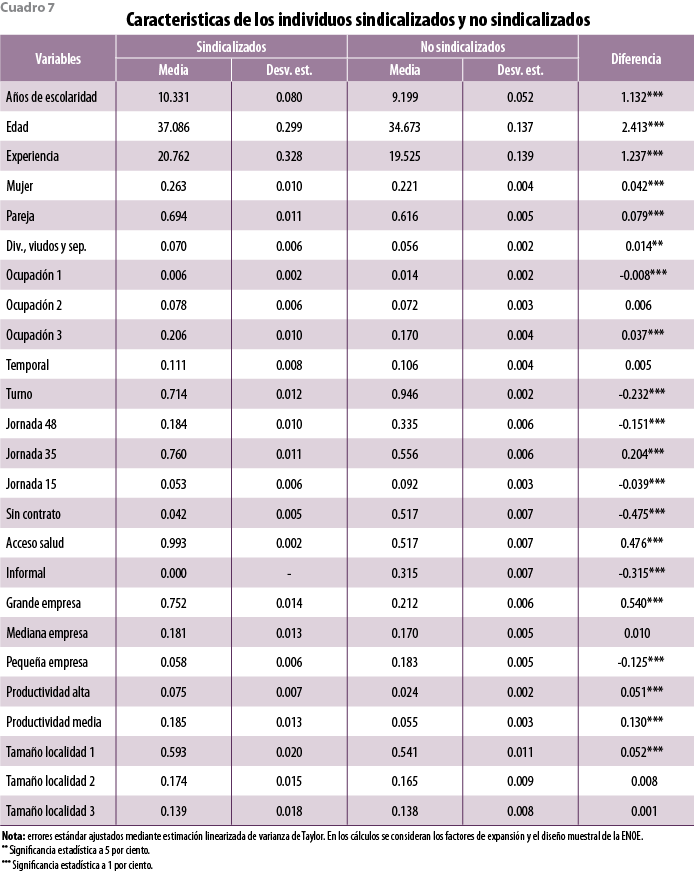
Como se puede observar en el cuadro 7 del apéndice, los sindicalizados (grupo de tratamiento) registran diferencias significativas en las variables que se muestran en relación con los no afiliados (grupo de control). Destaca que los trabajadores subordinados y remunerados en la industria en México que están afiliados a algún sindicato tienen una escolaridad y edad medias 1.1 y 2.4 años mayores que los no sindicalizados, respectivamente. Asimismo, tienden a tener pareja en una mayor proporción (69.4% frente a 61.6%). Los tipos de ocupación más frecuentes de los sindicalizados son los de oficinista, operador de transporte y trabajador en servicios personales. Al igual que los no afiliados, los que tienen afiliación sindical trabajan, en su mayoría, 35 horas a la semana, aunque en un porcentaje significativamente mayor. Como era de esperarse, el porcentaje de trabajadores sindicalizados con acceso a instituciones de salud es muy superior al de los no afiliados (99.3% frente a 51.7%). Tres cuartas partes del grupo de tratamiento trabaja en establecimientos de tamaño grande, a diferencia de 21.2% del de control. Otro aspecto relevante es que los trabajadores industriales habitan, en su mayoría, en localidades de más de 100 mil habitantes, 59.3% en el caso de los sindicalizados y 54.1% en el de los no sindicalizados.

En concordancia con las diferencias estadísticamente significativas observadas entre los grupos de tratamiento y control, a continuación se detallan los resultados de cuatro distintas especificaciones del PSM, las cuales buscan hacer comparables dichos grupos para obtener un estimador insesgado de la prima por sindicalización.

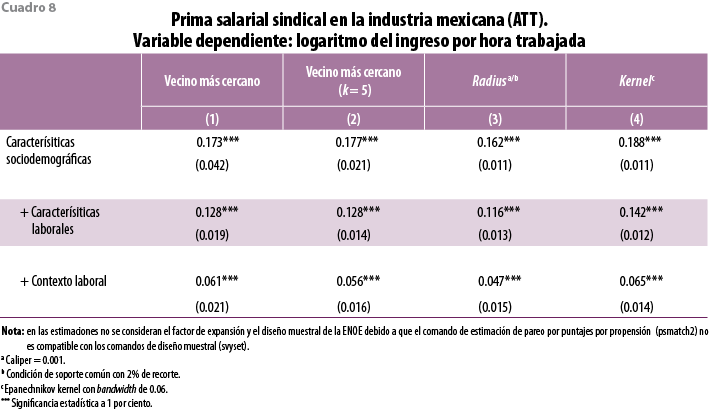
De acuerdo con las estimaciones de NNM, la prima salarial sindical es de 17.3% (ver cuadro 8 del apéndice); no obstante, al igual que en Blanchflower y Bryson (2004), este resultado se ve disminuido a 6.1% cuando se añaden variables del contexto laboral, lo cual sugiere que parte del incremento en el ingreso de los sindicalizados puede ser explicado por el hecho de que laboran en lugares con salarios más elevados en general, como las empresas grandes, en las que, de acuerdo con nuestros datos, trabaja 75.2% de éstos (ver cuadro 7 del apéndice). Para México, Fairris y Levine (2004) estiman la prima sindical en 19%, mientras que para EE.UU., Schmitt (2008) calcula que dicho diferencial es, en promedio, de 11.9%, aunque en ambos estudios no se agregan variables del contexto laboral.

La densidad sindical y, por lo tanto, el poder de negociación de los sindicatos han disminuido en México (Zepeda, 2009; Esquinca y Melgoza, 2006; Fairris y Levine, 2004; Herrera y Melgoza, 2003), lo que ha reducido, a su vez, la prima por sindicalización. Como referencia, Panagides y Patrinos (1994)¹⁶ estimaron que la brecha salarial entre sindicalizados y no sindicalizados era de 10.4% para 1989, por lo que existe una tendencia hacia la disminución en la PSS.

Nuestro resultado anterior es robusto ante diferentes especificaciones de PSM. La prima salarial sindical varía entre 16.2 y 18.8% (ver cuadro 8 del apéndice) cuando se consideran sólo las variables sociodemográficas individuales, mientras que cuando se controla por variables del entorno laboral, el impacto se ve reducido a 4.7% para el pareo Radius y 6.5% en el Kernel.

Por otra parte, las pruebas de balance muestran que, después del pareo, en todas las especificaciones de PSM se obtuvieron grupos de tratamiento y control estadísticamente comparables,¹⁷ sólo en el pareo Radius se rechazó la hipótesis de igualdad de medias para la variable de turno laboral.¹⁸

Además, casi en todas las variables, en los cuatro métodos de pareo, se alcanzaron porcentajes de sesgo aceptables; sólo en variables como el tipo de ocupación 3 (oficinistas, operadores de transporte o trabajadores en servicios personales), productividad alta y turno laboral, el porcentaje de sesgo se encuentra ligeramente por encima de 5 por ciento.

Conclusiones

En el presente estudio se destaca que el factor más importante para explicar la variación en las remuneraciones a los trabajadores es la educación, en especial una vez que se controla por endogeneidad. Los resultados se robustecieron controlando por las variaciones que ha experimentado el inicio del ciclo escolar y las fechas de nacimiento de los individuos. Esto sugiere que una simple estimación por mínimos cuadrados tiende a subestimar la relevancia de la educación, resultado que es congruente con la evidencia encontrada en estudios similares (ver Card, 2001).

Más aún, al comparar los resultados de esta investigación con estudios previos se encuentra que los rendimientos a la educación han tendido a reducirse en el tiempo. Rodríguez-Oreggia (2005) atribuye esta disminución a la falta de empleos adecuados para los trabajadores más calificados, además de que los empleos disponibles no necesariamente requieren de la obtención de un título. Por el contrario, Villarreal (2010) expone que los menores rendimientos se han acentuado para los menos calificados, ante el incremento en la demanda por los más educados; esto indica que no hay una explicación clara al respecto.

Además, se comprueba que los retornos a la escolaridad presentan diferentes matices por nivel de estudios alcanzados. En particular, se encuentra que existen pocos incentivos económicos para completar la educación básica, mientras que el retorno en los niveles de escolaridad más altos (con posgrado y universitarios) es significativamente alto. Estos resultados reafirman la necesidad de otorgar apoyos económicos para que los estudiantes decidan continuar sus estudios más allá del nivel de secundaria y realzan la importancia de la nueva legislación que hace obligatoria la educación media superior en México.

Como contribución a la evidencia sobre los determinantes de las remuneraciones, destaca la importancia que tiene la acumulación de experiencia laboral y el hecho de que, en el contexto mexicano, en las estimaciones de corte transversal se requiere controlar por las variaciones en los contextos laborales donde se desempeñan individuos de diferentes cohortes.

Respecto a la influencia de la variable sexo, el modelo verificó que, en promedio, las mujeres en la industria tienden a percibir salarios más bajos que los hombres. Esto puede atribuirse al tipo de trabajos de la población femenina en el sector industrial, en el cual, de acuerdo con nuestras categorías ocupacionales, ellas ocupan con mayor frecuencia que los hombres (23.5% frente a 15.7%) las de ingresos relativamente bajos, como oficinistas, operadores de transporte y servicios personales. Es preciso profundizar en las causas de este fenómeno indagando acerca de la influencia que puedan tener factores como la división del trabajo (dentro y fuera del hogar) por sexo o la existencia abierta de políticas discriminatorias en los centros de trabajo.

Por otra parte, la productividad de las unidades económicas influye en las remuneraciones sólo cuando está en un nivel cercano al promedio. La utilización de la productividad promedio de cada rama de actividad puede ocultar una cierta heterogeneidad al interior de la misma y generar, por consiguiente, información errónea sobre la relación entre ambas variables.

Se ha mostrado que existe una prima por trabajar en empresas de mayor tamaño debido, hipotéticamente, a las compensaciones otorgadas por este tipo de empresas a trabajadores más productivos, a su capacidad para absorber costos y repartir utilidades, así como al fomento a la estabilidad de los trabajadores más calificados mediante procesos de movilidad interna (Lallemand y Rycx, 2007).

Las estimaciones de la prima salarial sindical indican que los trabajadores afiliados reciben un ingreso por hora trabajada superior al de los no sindicalizados, lo cual puede ser explicado porque los primeros se encuentran vinculados con más frecuencia a establecimientos grandes, donde, como se constató, los ingresos promedio son mayores, además de que cuentan con un nivel medio de escolaridad relativamente alto.

Al igual que en Bryson (2002), se comprobó que cuando se adicionan variables del contexto laboral, la prima sindical se reduce de forma considerable; sin embargo, es recomendable incluir variables de composición del lugar de trabajo, como la proporción de mujeres o de trabajadores de tiempo parcial y la densidad sindical, aunque conviene tener presente que es muy probable que esta última se halle correlacionada con variables incluidas en las estimaciones usadas, como la productividad y el tamaño del establecimiento (de la Garza, 2002).

Los hallazgos anteriores apuntan hacia la importancia de incluir variables del lado de la demanda en los modelos tradicionales enfocados a los aspectos de oferta para explicar las remuneraciones. También, se desprende la importancia de impulsar una más efectiva vinculación de la educación con los requerimientos específicos de las actividades económicas, así como la necesidad de adoptar medidas orientadas a eliminar posibles barreras a la incorporación de las mujeres a ocupaciones de mayor jerarquía.

El trabajo indica la conveniencia de estructurar un aparato industrial integrado, en el que empresas de diferentes tamaños y actividades se vinculen por medio de relaciones técnicas que favorezcan una mayor homogeneidad de los niveles de remuneraciones entre tamaños de empresas.

Se encontró, asimismo, que los trabajadores informales cuentan con ingresos inferiores que los de la población ocupada en establecimientos formales; otros trabajos también muestran una relación negativa entre ambas variables, de donde se sigue que sería preciso eliminar los factores que alientan la informalidad y crear alicientes para el establecimiento y operación de empresas formales.

Por último, cabe aclarar que los resultados aquí analizados son válidos sólo para el periodo y grupo de población utilizados. Estudios similares han controlado por variables como el crecimiento económico y tasas de mortalidad para obtener estimaciones más reales que en el caso de modelos estáticos, como el que aquí se ha planteado.

Apéndice

Fuentes

Angrist, J. y A. Krueger. “Does Compulsory School Attendance affect Schooling and Earnings?”, en: Quarterly Journal of Economics. 106 (4), 1991, pp. 979-1014.

Arias, O., K. Hallock y W. Sosa. “Individual Heterogeneity in the Returns to Schooling: Instrumental Variables Quantile Regression using Twins Data”, en: Empirical Economics, Springer. 26 (1), 2001, pp. 7-40.

Arrow, K. J. “Higher Education as a Filter”, en: Journal of Public Economics. 2 (3), 1973, pp. 193-216.

Barceinas. F. “Endogeneidad y rendimientos de la educación”, en: Estudios Económicos. 18 (1), 2003, pp. 79-131.

Barragán, L. “¿Cuánto es el premio al salario por pertenecer a un sindicato en el Ecuador?: un análisis usando propensity score matching”, en: Revista Tecnológica ESPOL. 19 (1), 2006, pp. 217-224.

Bayard, K. y K. Troske. “Examining the Employer-Size Wage Premium in the Manufacturing, Retail Trade, and Service Industries Using Employer-Employee Matched Data”, en: American Economic Review. 89 (2), 1999, pp. 99-103.

Becker, G. Human Capital: A Theoretical an Empirical Analysis with Special Reference to Education. Tercera edición. 1993.

Blanchflower, D. y A. Bryson. “The Union Wage Premium in the US and the UK”, en: CEP Discussion Papers 0612. Centre for Economic Performance, London School of Economics and Political Science, 2004.

Blundell, R., L. Dearden y B. Sianesi. “Evaluating the Effect of Education on Earnings: Models, Methods and Results from the National Child Development Survey”, en: Journal of the Royal Statistical Society: Series A. 168 (3), 2005, pp. 473-512.

Booth, A., M. Coles y X. Gong. “Increasing Returns to Education: Theory and Evidence”, en: CEPR Discussion Paper 522. Centre for Economic Policy Research, The Australian National University, 2006.

Bratsberg, B. y F. Ragan. “Changes in the Union Wage Premium by Industry”, en: ILR Review. 56 (1), 2002, pp. 65-83.

Brown, F. y L. Dominguez. “Determinants of Wage Differentials in the Maquila Industry in Mexico: A Gender Perspective”, en: GEM-IWG Working Paper Series 07-06. The International Working Group on Gender, Macroeconomics and International Economics, 2007.

Bryson, A. “The Size of the Union Membership Wage Premium in Britain’s Private Sector”, en: PSI Discussion Paper 9 and PSI Report No. 886. London School of Economics and Political Science, 2002.

Bulow, J. I. y L. H. Summers. “A Theory of Dual Labor Markets with Application to Industrial Policy Discrimination and Keynesian Unemployment”, en: Journal of Labor Economics. 4 (3), 1986, pp. 376-414.

Card, D. “Estimating the Return to Schooling: Progress on Some Persistent Econometric Problems”, en: Econometrica. 69 (5), 2001, pp. 1127-1160.

Castelar, A. y L. Ramos. “Inter-industry Wage Differentials and Earnings Inequality in Brazil”, en: Estudios de Economía. 21 (9), 1994, pp. 79-111.

De la Garza, E. “México: macroeconomía, modelos de producción y relaciones entre dos siglos”, en: Transitions to Democracy in Mexico. Center on North America Politics and Society, University of Carleton, 2002.

Duarte, J. L. “Estimación de los retornos a la educación a partir de encuestas de hogares y algunos resultados para Colombia”. Mimeo. Universidad ICESI, 2012.

Esquinca, M. y J. Melgoza. “La afiliación sindical y premio salarial en México”, en: De la Garza, E. y C. Salas (coords.). La situación del trabajo en México 2006. Plaza y Valdés Editores, 2006.

Fairris, D. “¿Qué hacen los sindicatos en México?”, en: Estudios Económicos. 22 (2), 2007, pp. 185-240.

Fairris, D. y E. Levine. “La disminución del poder sindical en México”, en: El Trimestre Económico. 71 (4), 2004, pp. 847-876.

Harberger, A. C. y S. Guillermo. “Estimating Private Returns to Education in Mexico”, en: Latin American Journal of Economics. 49 (1), 2012, pp. 1-35.

Herrera, F. y J. Melgoza. “Evolución reciente de la afiliación sindical y la regulación laboral en México”, en: De la Garza, E. C. y Salas (coords.). La situación del trabajo en México 2003. Plaza y Valdés Editores, 2003.

Kling, J. “Interpreting Instrumental Variables Estimates of the Returns to Schooling”. NBER Working Paper Series No. 7989. National Bureau of Economic Research, 2000.

Lallemand, T. y F. Rycx. “Employer Size and the Structure of Wages: A Critical Survey”, en: Refletset Perspectives de la Vie Économique. 46 (2), 2007, pp. 75-87.

Leigh, A. y Ch. Ryan. “Estimating Returns to Education using Different Natural Experiment Techniques”, en: Economics of Education Review. 27 (2), 2008, pp. 149-160.

Lemieux, T. “The Mincer Equation Thirty Years after Schooling, Experience, and Earnings”, en: Grossbard, S. (ed.). Jacob Mincer, A Pioneer of Modern Labor Economics. Springer Verlag, Parte 4, 2006, pp. 127-145.

Leuven, E. y B. Sianesi. PSMATCH2: Stata Module to Perform Full Mahalanobis and Propensity Score Matching, Common Support Graphing, and Covariate Imbalance Testing. Version 4.0.5 (2012).

Lewis, W. A. “Economic Development with Unlimited Supplies of Labor”, en: The Manchester School of Economic and Social Studies. 22, 1954, pp. 139-191.

Mincer, J. A. “Schooling, Experience, and Earnings”, en: Columbia University Press. 1974.

López Acevedo, G. “Mexico: Evolution of earnings inequality and rates of returns to education (1988-2002)”, en: Estudios Económicos. 19 (2), 2004, pp. 211-284.

Moreno, J. “Los salarios en el sector formal e informal en México: análisis de ganancias y pérdidas por formalización”, en: Ensayos. Revista de Economía. 26 (1), 2007, pp. 1-44.

Muñoz, M. “Determinantes del ingreso y del gasto corriente de los hogares”, en: Revista de Economía Institucional. 6 (10), 2004, pp. 183-199.

Ordaz, J. “México: capital humano e ingresos. Retornos a la educación, 1994-2005”, en: CEPAL. Serie Estudios y Perspectivas-México. 90, 2007.

Panagides, A. y H. Patrinos. “Union-Nonunion Wage Differentials in the Developing World”, en: Policy Research Working Paper No. 1269. Latin America and the Caribbean, Country Department II, World Bank, 1994.

Popli, G. “Rising Wage Inequality in Mexico: Structural Reforms or Changing Labor Market Institutions?”, en: Sheffield Economic Research Paper Series No. 2005016. The University of Sheffield, 2005.

Rodríguez Oreggia, E. Institutions, Geography and the Regional Development of Returns to Schooling in Mexico. Instituto de Investigaciones sobre Desarrollo Sustentable y Equidad Social, Universidad Iberoamericana, 2005.

Rojas, M., H. Angulo e I. Velázquez. “Rentabilidad de la inversión en capital humano en México”, en: Economía Mexicana. Nueva Época. 9 (2), 2000, pp. 113-142.

Samuelson, P. A. “Paul Douglas´s Measurement of Production Functions and Marginal Productivities”, en: Journal of Political Economy. 87 (5), 1979.

Sarimaña, E. “Rendimiento de la escolaridad en México: una aplicación del método de variables instrumentales para 1988”, en: Gaceta de Economía. 7 (14), 2002, pp. 85-127.

Schmitt, J. The Union Wage Advantage for Low-Wage Workers. Center for Economic and Policy Research, 2008.

Spence, M. “Job Market Signalling”, en: The Quarterly Journal of Economics. 87 (3), 1973, pp. 355-374.

Staiger, D. y J. H. Stock. “Instrumental Variables Regression with Weak Instruments”, en: Econometrica. 65 (3), 1997, pp. 557-586.

Stiglitz, J. E. “Alternative Theories of Wage Determination and Unemployment in LDC’s: The Labor Turnover Model”, en: The Quarterly Journal of Economics. 88 (2), 1974, pp. 194-227.

Taubman, P. J. y T. J. Wales. “Higher Education, Mental Ability, and Screening”, en: Journal of Political Economy. 81 (1), 1973, pp. 28-55.

Urciaga, G. J. y M. A. Almendarez. “Determinación de los salarios y rendimientos de la escolaridad en la región Mar de Cortés”, en: Revista de la Educación Superior. 35 (2), 2006, pp. 37-53.

Varela, R. y A. Retamoza. “Los salarios en México: un análisis con datos de panel”, en: Investigación y Ciencia. 53, 2011, pp. 29-38.

Villarreal, E. M. “Evolución histórica de los rendimientos educativos en México: 1987-2009”, en: Mancebón, M. J., D. P.

Ximénez, J. M. Gómez y G. Giménez (eds.). Investigaciones de economía de la educación 5. Vol. 5, Capítulo 11, 2010, pp. 223-244.

Webbink, D. y J. van Wassenberg. “Born on the First of October: Estimating the Returns to Education Using a School Entry Rule”. Mimeo. University of Amsterdam, 2004.

Zamudio, A. “Rendimientos a la educación superior en México: Ajuste por sesgo utilizando máxima verosimilitud”, en: Economía Mexicana. Nueva Época. 4 (1), 1995, pp. 69-91.

Zepeda, R. “Disminución de la tasa de trabajadores sindicalizados en México durante el periodo neoliberal”, en: Revista Mexicana de Ciencias Políticas y Sociales. 51 (207), 2009, pp. 57-81.

¹ Incluye salarios y prestaciones, netos.

² Incluye manufacturas, construcción, electricidad, suministro de agua y gas, además de actividades extractivas.

³ En las estimaciones se toma en cuenta el diseño muestral de la Encuesta. Para ello, se utilizan las variables que identifican la unidad primaria de muestreo, así como los factores de expansión y de corrección por finitud.

⁴ Una vez aplicado el factor de expansión, esta cifra equivale a 8 820 298 trabajadores.

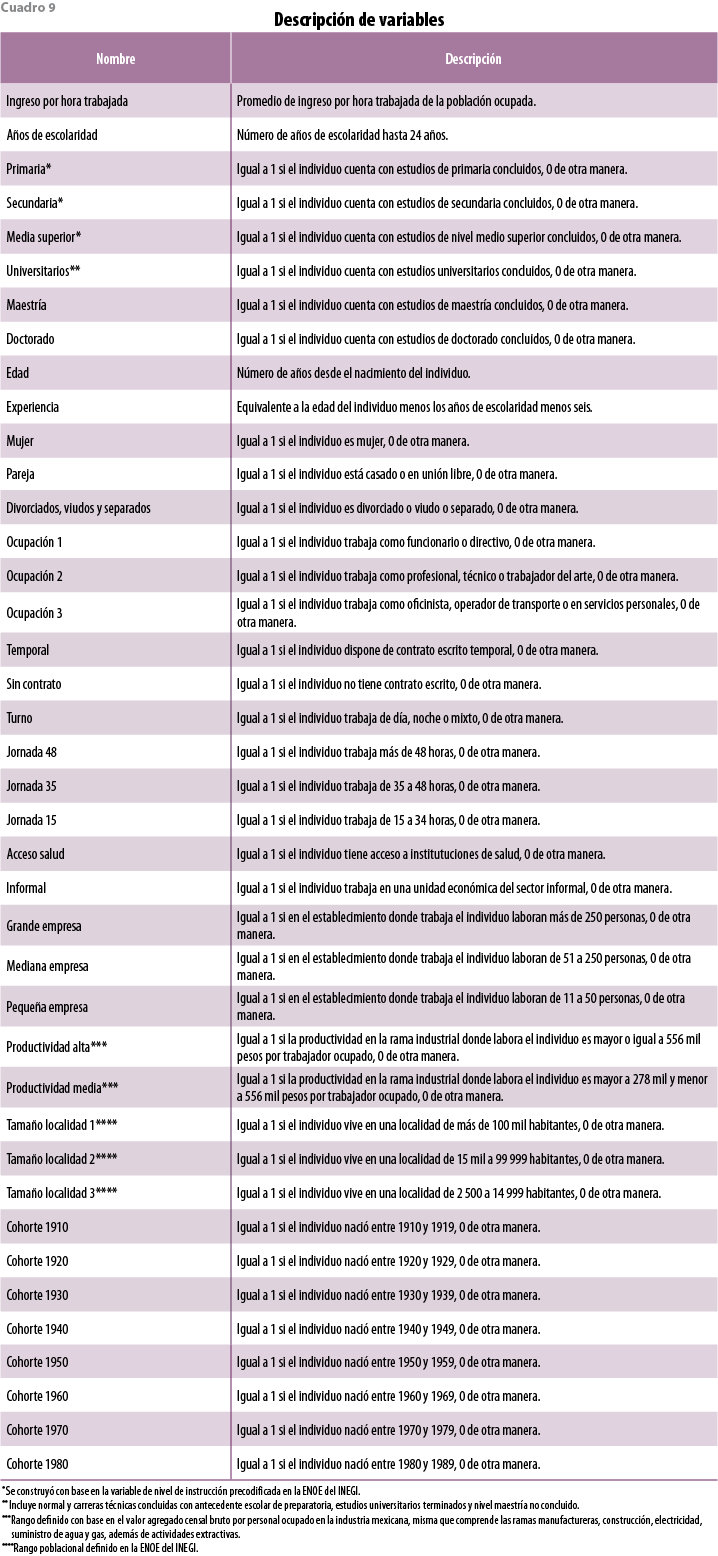
⁵ Variable estimada con base en datos de los Censos Económicos 2009 del INEGI. En el cuadro 9 del apéndice se describe esta variable (ver cuadro y sus notas a pie).

⁶ Como se menciona en Ordaz (2007) y Villarreal (2010), existen otros posibles errores de medición en las ecuaciones del tipo minceriano, como el sesgo por selección que se deriva del hecho que existan individuos cuya decisión de participar en el mercado laboral no sea aleatoria. En particular, Varela y Retamoza (2011) encuentran que la variable sexo es una condicionante para que los individuos (jefes del hogar, en este caso) decidan incorporarse al mercado laboral.

⁷ La ENOE permite vincular variables relevantes del contexto familiar (por ejemplo, escolaridad y ocupación de los padres) sólo para individuos que viven con sus padres, lo cual puede inducir cierto sesgo en las estimaciones.

⁸ Está claro que el mes de nacimiento puede estar correlacionado con otros factores, lo que aquí se señala es que el efecto sobre el ingreso se da de manera indirecta, a través de su efecto sobre la escolaridad de los individuos.

⁹ Leigh y Ryan (2008) agregan la variable de posición relativa al modelo, lo que permite medir los efectos sobre el aprendizaje en función del orden en que hayan nacido los miembros del grupo escolar. Sin embargo, dicha variable está muy correlacionada con el mes de nacimiento, por lo que no sería recomendable incluirla en las estimaciones.

¹⁰ Los cuadros con los resultados de las pruebas de balance antes y después del pareo en cada especificación de PSM a que se hará mención en los resultados pueden ser solicitados a los autores.

¹¹ Además de las variables que están muy correlacionadas por construcción (ejemplo: escolaridad y experiencia), el lector podrá observar en el cuadro 1 del apéndice que existen variables con coeficientes de correlación de alrededor de 30% (ejemplo: escolaridad e informalidad), los cuales se omite mencionar por la importancia de evaluar su efecto sobre las remuneraciones.

¹² La fórmula aplicada es , donde β_k es el coeficiente del efecto sobre el ingreso para el nivel educativo k, β_k-1 es el coeficiente para el nivel educativo, k-1 y n_k son los años de estudio para completar el nivel k. En este caso, los niveles k son primaria (seis años), secundaria (tres años), media superior (tres años), universitario (cinco años), maestría (dos años) y doctorado (tres años). Los valores de los coeficientes fueron tomados del cuadro 3 del apéndice.

¹³ Esto equivale a 1.4% por año de estudio.

¹⁴ El coeficiente de las estimaciones con fecha de corte 31 de diciembre no fue estadísticamente robusto.

¹⁵ Ver Card (2001) para profundizar en estas explicaciones.

¹⁶ Aunque en sus estimaciones emplean mínimos cuadrados ordinarios, estos autores controlan por el tipo de actividad industrial, por lo que sus resultados son comparables con los nuestros.

¹⁷ Al 5% de significancia, no se rechaza la hipótesis nula de igualdad de medias para todas las variables utilizadas de los grupos de sindicalizados y no sindicalizados.

¹⁸ Los resultados de las pruebas de balance antes y después del pareo en cada especificación de PSM pueden ser solicitados a los autores.