Percepción remota para la estimación de población en áreas geoestadísticas básicas

El volumen total de personas que forman una población es un insumo básico para diversos procesos de análisis previos al diseño de políticas públicas y de planes de ordenamiento territorial. Desafortunadamente, los censos de población y vivienda, que son la fuente más confiable para obtener dicha información, se realizan cada 10 años debido a los altos costos y tiempos requeridos, y aunque son escalonados con los conteos de población para alcanzar un intervalo de muestreo¹ de cinco años, la frecuencia resulta insuficiente, sobre todo en áreas territoriales con una acelerada dinámica poblacional. En estos casos, una estimación inicial rápida para años no censales supone una ventaja importante en la toma de decisiones. Por lo tanto, en esta investigación se planteó, como hipótesis general, que los sensores montados en plataformas aéreas o satelitales podrían aportar una solución consistente y de bajo costo.

La estimación de población en áreas pequeñas tiene una multiplicidad de metodologías que, por su naturaleza, han sido agrupadas en métodos basados en funciones matemáticas y en variables sintomáticas o indicadores. El primer grupo produce estimaciones de población que suelen ser muy útiles para calcular la población de áreas pequeñas que no cuentan con estadísticas vitales en periodos intercensales (González y Torres, 2012). Es recomendable que este grupo de métodos se aplique en lapsos que no excedan de 15 años y que el control de ajustes haga empleo de proyecciones de población (González y Torres, 2012, p. 108). Los métodos basados en variables sintomáticas, llamados de esa forma porque se sustentan en encontrar información disponible de variables que se encuentran relacionadas de alguna manera al volumen y cambios de una población (González y Torres, 2012, p. 105). Entre las variables que se han empleado destacan los registros de consumidores de servicios básicos (agua y electricidad), las matrículas escolares, los registros electorales y las estadísticas de construcciones habitacionales (González y Torres, 2012, pp. 115-116).

El ejercicio que aquí se presenta es una variación de los métodos de variables sintomáticas, pues busca asociar el número total de habitantes con ciertos aspectos observables de la población mediante el uso de percepción remota. Por su parte, la estimación de población a través de datos de percepción remota y sistemas de información geográfica (SIG) no es una novedad. No obstante, un vistazo a la literatura disponible sobre el tema revela que la gran mayoría de los estudios ha empleado datos provenientes de sensores de resolución baja (alrededor de 1 km por pixel), como DMSP y AVHRR (Yang, Yue y Gao, 2013; Sutton, P., 2000; Sutton, Roberts, Elvidge y Melj, 1997; Dobson, Brlght, Coleman, Durfee y Worley, 2000) y, sobre todo, de resolución moderada (entre 10 y 100 metros por pixel), como los sensores de la serie Landsat (Azar, Engstrom, Graesser y Comenetz, 2013; Wu y Murray, 2007; Lu, Weng y Li, 2006; Harvey, 2002; Iisaka, 1982). Dentro del primer grupo se encuentran aquellos estudios que se enfocan a la estimación de población a nivel regional y global, mientras que en el segundo están los que hacen estimaciones a nivel de ciudades y regiones. También, es interesante notar que, en una escala regional, el principal indicador de población suele ser el área de los asentamientos, en tanto que en una escala de ciudad o localidad se tienden a emplear los de áreas de superficie impermeable, tipos de coberturas o usos de suelo.

Los estudios de estimación de población para áreas pequeñas (como manzanas o AGEB) incluyen, por lo general, el uso de imágenes de resolución espacial alta (de alrededor de 1 metro por pixel), entre las que sobresale la fotografía aérea, que cuenta con una larga tradición que ha evolucionado de los formatos analógicos a los digitales. En México se tiene como antecedente de su uso para este fin un estudio realizado por El Colegio de México (COLMEX), AC (Ordorica e Ibarra, 2002), en el cual se estimó la población de la Villa Milpa Alta mediante el ajuste del filtro de Kalman a series históricas de población (1970-2000) y área del asentamiento para las distintas fechas de los censos. En ese caso, el área se extrajo delineando sobre fotografías aéreas los límites del asentamiento urbano.

Con el lanzamiento de IKONOS en 1999, considerado como el primer satélite civil de resolución espacial alta, se inició una etapa de exploración de metodologías automatizadas para estimar población en áreas pequeñas. De esto da cuenta un incremento exponencial en el número de publicaciones sobre el tema a partir de entonces (ver gráfica 1). Este acelerado aumento también se explica por la amplia disponibilidad de herramientas de análisis espacial en los SIG, los cuales permitieron integrar datos vectoriales con datos en formato raster, que es el nativo de las imágenes.

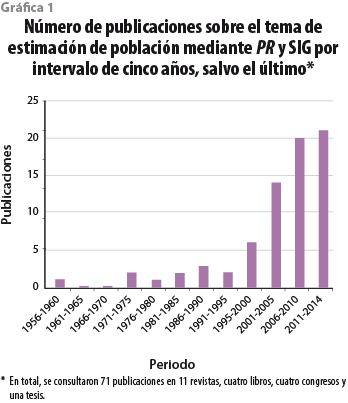
Entre los sensores satelitales multiespectrales de alta resolución espacial que se consideran en esta categoría, se encuentran IKONOS (1 m de resolución en la pancromática), QuickBird (0.6 m), WorldView-2 (0.5 m) y Geoeye-1 (0.4 m). De las 71 publicaciones consultadas, 13 reportaron el uso de imágenes satelitales de alta resolución espacial, donde IKONOS y QuickBird destacan como las de mayor uso, ya sea solas o en combinación con otro tipo de datos. Este número se duplica si se consideran estudios que emplearon fotografías aéreas, datos de catastro o mapas topográficos detallados con información de edificios.

Si bien la estimación de población en áreas pequeñas se lleva a cabo de forma típica a partir de dos enfoques (mediante el conteo de unidades de viviendas y la determinación de áreas de viviendas), en fechas recientes, en algunos países (como Japón) se han empleado datos de catastro actualizados para estimar población utilizando no sólo el área y número de edificios, sino también el número de niveles (Lwin y Murayama, 2009).

Con el advenimiento del sensor LIDAR se pudieron hacer mediciones en tres dimensiones, tanto del terreno como de los elementos sobre él. No obstante que los escáneres por láser se crearon en la década de los 90, su aplicación para la estimación de población es muy reciente (la referencia más antigua data del 2010). En este tipo de modelos se suele incorporar el volumen de edificios como variable sintomática, de tal forma que ya no sólo es necesario el conteo o delineado de áreas construidas, sino también la estimación de su altura y/o el número de niveles (Silván-Cárdenas, L. Wang, Rogerson, Feng y Kamphaus, 2010; Qiu, Sridharan y Chun, 2010; Sridharan y Qiu, 2013; Lwin y Murayama, 2011).

Con estos antecedentes, se planteó un proyecto cuyo objetivo fue desarrollar y probar una metodología de estimación de población en las áreas geoestadísticas básicas empleando imágenes de alta resolución espacial y datos de altimetría LIDAR para la ciudad de México. El problema se abordó a partir del planteamiento de dos hipótesis interrelacionadas:

Mientras que la primera asume de manera implícita que la población que no habita en viviendas es una fracción muy pequeña del total poblacional (en todo caso, es proporcional a la población que sí lo hace), la segunda asume que la manifestación física de cada vivienda es cuantificable. De ser el caso, la población podría estimarse a partir del número de viviendas, el cual se calcularía a su vez a partir de los espacios habitacionales detectados con percepción remota.

El resto del documento describe el desarrollo y prueba de modelos empíricos que intentan probar o refutar las dos hipótesis. En primer lugar, se introducen ambos modelos; en segundo, se describe el área de estudio y el procesamiento de los datos de catastro y de percepción remota para el cálculo de variables sintomáticas; después, se presentan y analizan los resultados de la evaluación de los modelos y, por último, se dan las conclusiones y reflexiones derivadas del estudio.

Modelos de estimación de población

Para probar la primera hipótesis, se desarrollaron cinco modelos regresivos de población con número de viviendas como variable independiente (ver tabla 1).

Los modelos P1 y P2 relacionan de forma directa el número de unidades de vivienda con la población total en una misma fecha. Mientras P1 establece una relación lineal entre las variables, el modelo P2 establece una relación logarítmica que se deriva de la ley de crecimiento alométrico. En Biología, la ley de crecimiento alométrico establece que el incremento relativo de un organismo es proporcional al incremento relativo de un órgano. En el contexto geográfico, se ha mostrado que la población tiende a obedecer una relación similar con el tamaño del asentamiento (Nordbeck, 1965; Nordbeck, 1971), la cual se puede hacer más específica al considerar el número de viviendas en lugar del tamaño del asentamiento. Si, además, se considera que las variables son continuas, se puede plantear la relación en función de derivadas, lo que resulta en una ecuación diferencial cuya solución expresa una relación lineal entre los logaritmos de las variables. El modelo P2 presenta una ligera variación de la ley de crecimiento alométrico porque se suma 1 a las variables para evitar logaritmos con 0.

Los modelos P3, P4 y P5 representan otras variaciones que relacionan el incremento de la población con el aumento de unidades de viviendas pero, a diferencia de P2, éstos mantienen el carácter discreto de los incrementos; por ejemplo, el P5 relaciona los crecimientos normalizados por la suma de las poblaciones de las dos fechas, lo que equivale a un incremento relativo a la población promedio del periodo.

Modelos de estimación de viviendas

Para probar la hipótesis dos, se desarrollaron 10 modelos, los cuales resultan de combinar dos tipos de relación (con y sin transformación de variables) con cuatro tipos de variables independientes, las cuales son: 1) número de edificios con uso de suelo exclusivamente habitacional, 2) área habitable² de edificios con uso de suelo habitacional, 3) área habitable de edificios con usos de suelo seleccionados óptimamente y 4) área habitable total sobre todos los usos de suelo disponibles. Las expresiones explícitas de cada modelo se proporcionan en la tabla 2, junto con una breve descripción.

Los modelos V1 y V3 están inspirados en los tradicionales que relacionan el número de viviendas y el volumen construido, en ese orden. No obstante, en lugar de emplear el volumen, se emplea el área de la planta multiplicada por el número de niveles, cantidad denominada como área habitable. Así, si la altura de entrepisos fuera la misma para todos los edificios, el área habitable resultaría ser proporcional al volumen envolvente del edificio. En nuestro caso, esta altura no es constante, tal como se muestra más adelante. Los modelos V2 y V4 corresponden a las versiones con trasformación logarítmica de las variables, como extensión de la ley de crecimiento alométrico.

Los V5 y V6 son, en principio, modelos con múltiples variables que representan el área habitable de edificios con distintos usos de suelo. Con ello, se presupone que la población puede vivir en edificios con uso de suelo reportado en catastro distinto al exclusivamente habitacional. Más aún, en lugar de seleccionar a priori los usos de suelo donde la población podría estar alojada, éstos se determinan a partir de una muestra estadística. Esto se hizo mediante el método de selección de variables conocido como regresión lineal por pasos (Efroymson, 1960). Se trata de un algoritmo iterativo que incorpora y retira variables del modelo en función de su desempeño. Hay dos parámetros claves que controlan la entrada y salida de variables del modelo: 1) la probabilidad de entrada y 2) la probabilidad de salida, las cuales son de significancia estadística de una variable. En el caso del modelo V6, primero se debe expresar el modelo en forma lineal vía logaritmos y después se aplica la regresión lineal por paso a las variables transformadas.

Los modelos V7 a V10 asumen que la información de uso de suelo no es relevante para la estimación de población. Éste puede ser el caso cuando, en el área de estimación, existe una mezcla muy homogénea de usos de suelos, de tal forma que el área habitable de la totalidad de los edificios guarda una proporción directa con el área habitable de edificios donde se aloja la población. Mientras los modelos V7 y V8 son estáticos, como todos los anteriores, los V9 y V10 son dinámicos porque relacionan los incrementos de viviendas con aumentos del área habitable. Por su parte, los V8 y V10 corresponden a las versiones con transformación de variables. En el caso de V10 se emplea la raíz cúbica en lugar de logaritmos; esto fue inspirado por la interpretación del exponente de una relación alométrica que, de acuerdo con Nordbeck (1971), correspondería al cociente de las dimensiones de las variables. Por ejemplo, el exponente b, en una relación alométrica de la forma A =aP^b entre el área A de un asentamiento y la población total P, por lo general se aproxima a 2/3. Se presume que esto se debe a que mientras el área es una variable de dos dimensiones, la población representa un volumen de tres (Nordbeck, 1971). En otras palabras, la relación que guardaría la raíz cúbica de la población con la raíz cuadrada del área del asentamiento es en esencia lineal. En el caso del modelo V10, tanto el aumento del número de viviendas como el incremento del área habitable son variables volumétricas, por lo que las raíces cúbicas representan variables unidimensionales que estarían relacionadas de forma lineal.

Selección de áreas de estudio y preparación de los datos

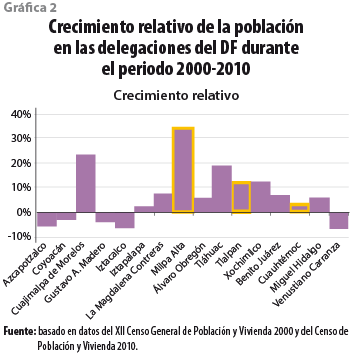
Con el fin de probar los modelos en condiciones de densidad y ritmo de crecimiento diversos, se seleccionaron tres delegaciones representativas de un núcleo densamente poblado con bajo crecimiento relativo, un área periurbana con crecimiento moderado y una rural con crecimiento acelerado: Cuauhtémoc, Tlalpan y Milpa Alta, respectivamente. La gráfica 2 muestra el incremento relativo en la población entre el 2000 y 2010 para las 16 delegaciones del DF. Se resaltan en amarillo las que corresponden a las delegaciones seleccionadas para el estudio, aquéllas con decremento poblacional se descartaron debido a que, se presume, la dinámica de la poblacional no estaría ligada a la del crecimiento urbano de esas demarcaciones, sino a otras específicas, como: la especialización del uso del suelo, el encarecimiento del suelo intraurbano y la posterior gentrificación,³ además del crecimiento suburbano, entre otras.

Una vez seleccionadas las áreas de estudio, se obtuvo la geometría de AGEB para cada una de ellas, así como los datos de población y vivienda de los censos del 2000 y 2010 (INEGI, 2010 y 2000). Éstos fueron ligados a la geometría de AGEB en un sistema de información geográfica. Para ello, se tomó como base la geometría del 2010 debido a que es la más completa y precisa, por lo que todos los atributos se anexaron a ella. El ligado de los datos se hizo vía las claves de AGEB, de tal forma que a las que no existían en el 2000 se les asignaron valores de 0 en los atributos de población y vivienda del 2000. Además, se encontraron dos AGEB en el 2000, una en Tlalpan y otra en Milpa Alta, que se subdividieron en el 2010; en este caso, se hizo una asignación del dato del 2000 proporcional al área de las AGEB del 2010.

Cuantificación del área habitable

Además de anexar a la geometría base los atributos para el total de la población y el número de viviendas, se anexaron también otros para la cantidad de edificios y el área habitable por categoría de uso de suelo, los cuales fueron calculados a partir de datos del catastro y de percepción remota.

Los datos del catastro, con actualización al 2000, incluyeron polígonos de área construida con el número de niveles, así como polígonos de predio con la clave de uso de suelo. De la clave de uso de suelo, sólo se utilizó la primera letra que representa el uso de suelo principal, de tal forma que se ignoraron variaciones de un mismo uso o usos mezclados. Fue así como se generó una clasificación de predios en 27 categorías de uso de suelo. El área habitable se calculó primero por polígonos de área construida y luego se agregó por polígonos de predio. En el nivel de predio se combinó con la información de uso de suelo para después ser agregada a nivel de AGEB para cada uso de suelo por separado y para el total. El mismo procedimiento se siguió para el número de edificios.

Ya que no se contó con una versión del catastro actualizada al 2010, se generó una capa de áreas construidas que se detectaron a partir de datos de altimetría LIDAR e imágenes multiespectrales, todos adquiridos a finales del 2007. Aunque la fecha de adquisición de los datos de PR no coincidió con los datos del censo del 2010, se estimó suficiente debido a que, en promedio, los edificios se construyen en 12 meses y se habitan de dos a cinco años para asegurar rentabilidad inmobiliaria. A partir de los datos LIDAR, se estimó el número de niveles y se probó la viabilidad para actualizar la información de uso de suelo con base en características de los edificios y otras variables derivadas. Los resultados de estas pruebas fueron publicados de forma previa (Silván-Cárdenas, Almazán-González y Couturier, 2014). La extracción del uso de suelo mostró ser muy difícil, incluso con una taxonomía relativamente simple, por lo que en este estudio se consideró sólo la información del uso de suelo disponible en el catastro del 2000. A partir de esta información se generaron los indicadores de área habitable y número de edificios, tal como se hizo con los polígonos del catastro.

Extracción de áreas construidas

Ésta consistió en una serie de pasos que se describen de forma breve en esta sección. En el primero se generó un modelo digital de alturas (MDA) a partir de la nube de puntos LIDAR, siguiendo una metodología previamente publicada (Silván-Cárdenas y Wang, 2014; Silván-Cárdenas, J., 2013). En el segundo se empleó la imagen multiespectral QuickBird para identificar áreas de vegetación a partir del índice normalizado de vegetación (NDVI, por sus siglas en inglés). Las áreas de vegetación son excluidas del MDA, con lo que se obtiene un modelo digital de alturas de edificios.

En el tercer paso, con el fin de delimitar las áreas construidas, se estimó la magnitud del gradiente del MDA mediante el filtro de Sobel empleado para la detección de bordes en el procesamiento digital de imágenes. De forma previa se había desarrollado una metodología de extracción de áreas construidas a partir del modelo digital de alturas en formato raster (Silván-Cárdenas y Wang, 2011). En ese método, los pixeles son clasificados en edificado y no edificado, basado sólo en medidas texturales, lo que por lo general produce una máscara de edificios con contornos complejos y ruidosos. En cambio, en esta investigación, primero se aplicó el método de segmentación por cuencas a la magnitud del gradiente del MDA. Luego, se simplificaron los segmentos a partir de una serie de criterios empíricos antes de ser convertidos a polígonos. Por ejemplo, los segmentos con altura menor a 2 metros se eliminan, ya que éstos, por norma, no podrían constituir área habitable.⁴ Asimismo, los segmentos aislados de áreas menores a 16 metros cuadrados se eliminan por un razonamiento similar.⁵ Por otro lado, si estos segmentos pequeños son interiores a otros más grandes, no se eliminan sino que se unen con éstos, ya que los primeros suelen representar estructuras en azoteas, como: tinacos, tanques estacionarios, pequeñas bodegas, etcétera.

Por último, la segmentación resultante se convirtió a formato vectorial para ser incorporada en el SIG (ver imagen 1). A los polígonos así generados se le anexaron los valores de área y de altura media, así como el número de niveles que se estimó usando el modelo que se describe a continuación.

Estimación del número de niveles

A partir de alturas estimadas por LIDAR para las áreas construidas según el catastro, se construyó un modelo que permitió estimar el número de niveles de edificios. Para ello, se analizó el diagrama de dispersión entre el número de niveles del catastro y las alturas estimadas. Dada la discrepancia temporal entre ambos parámetros, uno debería esperar cierta dispersión, pero también una tendencia predominante debido a que, de manera presumible, la gran mayoría de áreas construidas no sufrieron cambios en el lapso de ocho años; por lo tanto, el modelo que describe la relación entre las variables debe ajustarse precisamente a los puntos alojados alrededor de dicha tendencia (ver gráfica 3).

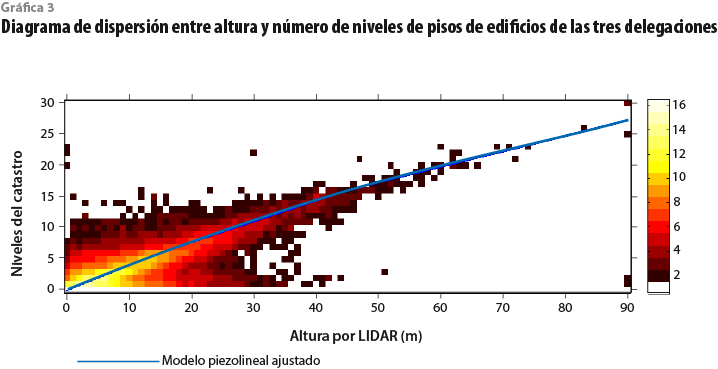
Para esta investigación, se ajustaron de forma visual tres segmentos lineales en tres distintos rangos de alturas (línea azul en la gráfica 3); el conjunto de los segmentos describe, precisamente, el modelo de estimación, el cual se puede expresar mediante la siguiente ecuación:⁶

donde n y h denotan el número de niveles y la altura, en ese orden, y los corchetes significan redondeo al entero más cercano.

Es interesante notar que los coeficientes del modelo indican que la altura de entrepiso para edificios de cinco pisos o menos es de 2.5 metros, mientras que para edificios de entre seis y 15 pisos es de 3 metros y para más de 15 pisos, de 4 metros. Además, las constantes que se suman representan los niveles que no contribuyen a la altura del edificio, esto es, los de sótanos. Así, los edificios de entre seis y 15 pisos tienen al menos un piso bajo el nivel del terreno, mientras que los de más de 15 cuentan con alrededor de cinco pisos bajo el nivel del terreno. Estos valores no reflejan necesariamente los rangos de valores de altura libre y niveles de sótanos establecidos en el Reglamento de Construcciones para el Distrito Federal (Arnal, 2005),⁷ ya que resultan de una observación estadística sobre una gran cantidad de edificios de diferente tipo y que fueron construidos con un amplio rango de valores posibles.

Medidas de desempeño de los modelos

Tanto para los modelos de estimación de población como para los de viviendas se definieron métricas para cuantificar la bondad de ajuste y la capacidad de generalización. Éstas incluyen:

Para cada delegación, se escogieron de manera aleatoria a lo sumo 50 AGEB, pero no más de dos terceras partes del total, las cuales fueron empleadas como muestra de calibración, mientras que el resto se emplearon como muestra de validación. El estadístico R2 se calculó sobre la muestra de calibración, mientras que las métricas MAE y MARE se calcularon sobre la muestra de validación. Para el cálculo de MARE, se excluyeron las divisiones entre 0 para evitar indeterminación.

Resultados

Las tablas de atributos con claves de AGEB se importaron en Excel y luego se calcularon los incrementos absolutos y relativos, y demás transformaciones, de las variables requeridas para linealizar los modelos (ver tablas 1 y 2). La estimación de parámetros de todos los modelos, con excepción de V5 y V6, se hizo a partir de la regresión simple en Excel 2010 (Microsoft Corp.). Para el caso de los modelos V5 y V6, se aplicó la implementación de la regresión lineal por paso (stepwisefit) disponible en el ToollBox Statistics de MATLAB (The Mathworks Inc.). En estos casos se emplearon los valores de probabilidad de entrada y salida de variables de 0.01 y de 0.02, respectivamente. Para el cálculo final, las estimaciones de los modelos fueron redondeadas al entero más cercano y los valores negativos reasignados con 0.

Estimación de población con viviendas del censo

Los valores de las medidas de desempeño de cada modelo se presentan en las tablas 3, 4 y 5 para las delegaciones Cuauhtémoc, Tlalpan y Milpa Alta, respectivamente. También, muestran los coeficientes (A y B) de cada modelo linealizado.⁸ En términos del ajuste, se observó que los modelos P1 y P2 ajustaron bastante bien los datos de las tres delegaciones (R2 > 0.91), el modelo P3 obtuvo el peor ajuste en los tres casos (R2 < 0.85), mientras que los modelos P4 y P5 sólo ajustaron de manera aceptable los datos de Tlalpan y Milpa Alta. Estas observaciones sugieren que el enfoque incremental implícito en estos modelos resulta menos apropiado para la Cuauhtémoc. En otras palabras, la dinámica demográfica en esta delegación parece no estar en sincronía con la dinámica de la vivienda. Para entender esto, basta recordar que la Cuauhtémoc perdió población residente a partir del sismo de 1985 (de 1980 al 2010 perdió 34.74%) y sólo del 2000 al 2010 ha comenzado a ganarla, pero en una proporción muy baja. De forma adicional, hubo un crecimiento de establecimientos comerciales, bodegas y oficinas (sobreespecialización del suelo). Este cambio de giro se ha dado muchas veces fuera del marco legal, propiciando que no esté consignado en los registros del catastro, es decir, muchos de los usos del suelo que dicen habitacional no corresponden a vivienda, sino a oficinas, bodegas o comercios. Del mismo modo, ha sucedido en la colonia Condesa (del 2000 al 2010 perdió 10.35% de su población); para el 2010, 15.74% de la vivienda estaba deshabitada o era usada para un giro diferente al habitacional (Salinas Arreortua, 2013).

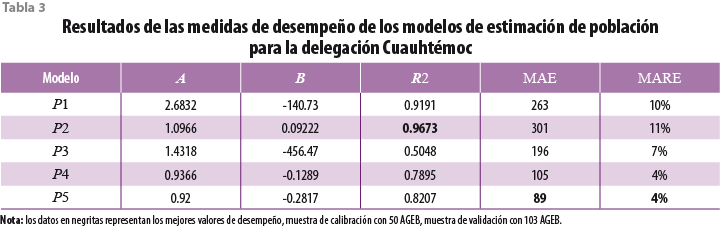
No obstante, en términos de la capacidad de generalización, medida a través de las métricas del error de estimación MAE y MARE, los resultados fueron distintos. Los modelos P4 y P5 presentaron valores de errores relativamente más bajos para las tres delegaciones, mientras que P1 y P2 lo hicieron sólo para Milpa Alta. Esta aparente contradicción en realidad indica que los modelos que ajustaron mejor la muestra de calibración estimaron peor la muestra de validación y viceversa.

Para propósitos de estimación, se prefiere el modelo P5 porque fue el que mejor estimó la población y el que resultó ser prácticamente insensible al cambio de densidad de la población, manteniendo un error de 5% en términos relativos y de entre 58 y 124 personas por AGEB en términos absolutos. La gráfica 4 muestra los diagramas de dispersión entre los valores observados y los estimados mediante este modelo. La gran mayoría de puntos caen alrededor de la línea de estimación perfecta, con lo cual se puede asumir que se valida la hipótesis 1. No obstante, hay casos anómalos que no cumplen con ella; por ejemplo, en el caso de la delegación Cuauhtémoc, el punto sobre la línea horizontal (vea el panel superior izquierdo de la gráfica 4) y corresponde a una AGEB en Tlatelolco que presentó una reducción en el número de viviendas (de 1 210 en el 2000 a sólo 70 viviendas en el 2010) y, en contraste, su población creció de forma ligera de 3 281 a 3 596 personas en el mismo periodo. Evidentemente, se trata de un caso anómalo que deberá analizarse con mayor cuidado. De manera adicional, hubo casos que no fueron representados de forma apropiada por el modelo, los cuales corresponden a las AGEB de reciente creación que se encontraron en Tlalpan y Milpa Alta, donde no fue posible cuantificar un incremento relativo, por lo que el modelo arrojó valores nulos de población.

Estimación de viviendas mediante datos de edificios

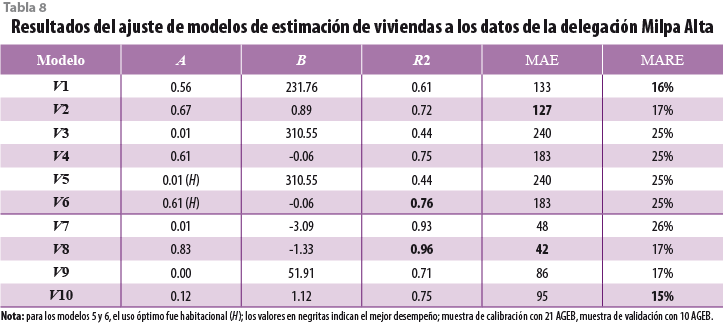
La prueba de los modelos V1 a V6 se hizo con datos del catastro del 2000, mientras que la prueba de los modelos V7 a V10 empleó los datos de PR del 2007. Esto fue necesario debido a que el primer grupo de modelos requiere información de uso de suelo confiable con la cual sólo se contó para el 2000. Además, los modelos V8 y V10, que son incrementales, requirieron tanto los datos del catastro como los derivados de PR. Los resultados obtenidos para las delegaciones Cuauhtémoc, Tlalpan y Milpa Alta se muestran en las tablas 6, 7 y 8, respectivamente.

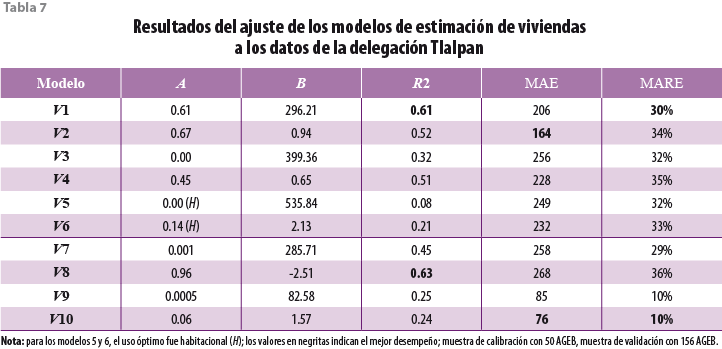
Para los modelos que incorporan la información de uso de suelo, se observó una clara distinción de la delegación Cuauhtémoc de las otras dos; en el caso de ésta, el modelo V₅ fue el que presentó mejores cifras de ajuste y error. Este modelo incorpora una selección óptima de usos de suelo, los cuales resultaron ser habitacional, espacios abiertos y públicos. Es interesante notar que todos los usos seleccionados tienen una contribución positiva en la estimación de las viviendas, lo cual sugiere que el uso de suelo podría estar desactualizado en el sentido de que ciertos espacios abiertos son, en realidad, de uso habitacional o, incluso, que son irregulares. Esto es menos probable en el caso de los espacios públicos y, por el valor relativamente pequeño del coeficiente, es posible que se hayan censado algunas viviendas en espacios públicos.

Por otro lado, en el caso de las delegaciones Tlalpan y Milpa Alta, el uso de suelo óptimo para el modelo V₅ fue sólo habitacional, lo que indica que la relación entre las viviendas y los edificios es mucho más simple que en la Cuauhtémoc. Más aún, los modelos sobresalientes para estas delegaciones fueron los V1 y V2, los cuales relacionan el número de edificios con el de viviendas. Esto sugiere que hay poca variabilidad en el tamaño de los edificios de vivienda en estas delegaciones, lo cual podría ser porque predominan las casas unifamiliares sobre los edificios multifamiliares.

En el caso de los modelos que no requieren información de uso de suelo, se ajustó mejor el modelo V8 seguido del V7, sobre todo en Milpa Alta. El primero se ajustó, incluso, mejor que los que incorporaron el uso de suelo, salvo para la delegación Cuauhtémoc, donde el ajuste del modelo V8 (R2 = 0.52) fue menor que el del V5 (R2 = 0.69). Lo anterior sugiere que la información de uso de suelo mejora el ajuste sólo si la demarcación presenta una fuerte sectorización en el uso de suelo, como es el caso en la Cuauhtémoc, donde se encuentran corredores comerciales, colonias habitacionales, etcétera.

En contraste al nivel de ajuste, la capacidad de generalización de los modelos ocurre a la inversa, es decir, los modelos V9 y V10 presentaron errores más bajos que los V7 y V8. En términos del error relativo, destaca el desempeño consistentemente superior del V10 con las tres delegaciones (MARE ≤ 18%). Esta aparente contradicción indica en realidad que los modelos V7 y V8 tienden a sobreajustar los datos, lo cual no ocurre con los V9 y V10.

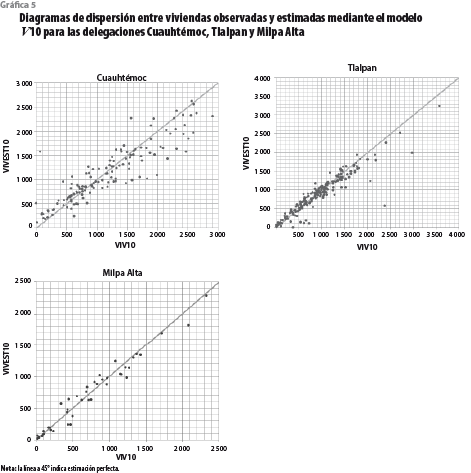
En términos de la capacidad de generalización, el desempeño del modelo V10 resultó superior incluso que el mejor modelo con información de uso de suelo. La gráfica 5 presenta los diagramas de dispersión entre las estimaciones del modelo V10 y los valores de vivienda del censo. Las AGEB que presentaron desviaciones significativas respecto a la línea de estimación perfecta fueron sobre todo aquéllas donde se observó un crecimiento en sentido contrario al del área habitable. De forma más específica, los errores de estimación estuvieron correlacionados de manera negativa al incremento de número de viviendas, con valores para el coeficiente de correlación de Pearson de -0.6, -0.8 y -0.6 para las delegaciones Cuauhtémoc, Tlalpan y Milpa Alta, respectivamente. Así, a mayor decremento en el número de viviendas hay, por lo general, un mayor error de estimación.

Estimación de población con viviendas estimadas

De los resultados reportados con anterioridad es claro que la composición P5-V10 define la mejor opción para la estimación de la población. No obstante, en esta investigación se probó el desempeño de las combinaciones del modelo P5 con V7, V8, V9 y V10; estos cuatro modelos se eligieron porque: 1) son los que incorporaron los datos de percepción remota y 2) son los que obtuvieron el mejor desempeño en términos del error absoluto. Los errores de estimación de estas pruebas se presentan en la tabla 9.

Como era de esperarse, los errores de estimación de viviendas se transfirieron a la estimación de población, incrementando con respecto a los observados cuando se emplearon los valores censales del número de viviendas. El peor desempeño se observó para modelos no incrementales (V7 y V8), que alcanzaron valores relativos de hasta 39%, mientras que el mejor se observó para los incrementales (V9 y V10), los cuales presentaron errores por debajo de 18% en términos relativos y de entre 288 y 317 personas en absolutos. Consistente con el desempeño observado para los modelos de estimación de vivienda, el mejor para la estimación de la población fue la composición P5-V10, exhibiendo errores relativos de 15% para la delegación Cuauhtémoc, 14% para Milpa Alta y 12% para Tlalpan.

La distribución espacial del error relativo de las estimaciones hechas mediante la composición P5-V10 para las delegaciones Cuauhtémoc, Tlalpan y Milpa Alta se muestran en las imágenes 2, 3 y 4, respectivamente; en éstas se puede observar que diferentes tipos de errores se concentran en diferentes áreas. Al compararlos con las de uso de suelo, se observó cierta concordancia con la distribución del uso de suelo habitacional. En específico, se observó que las AGEB con predominancia de uso de suelo habitacional presentaron una subestimación entre 10 y 50%, mientras que aquéllas con predominancia de uso de suelo no habitacional se sobrestimó la población en diferentes proporciones. En general, lo errores se deben a las mismas causas que en el caso de estimación de vivienda.

Discusión

El presupuesto ejercido por el INEGI para el Censo de Población y Vivienda 2010 ascendió a 4 437.96 millones de pesos (mdp); si este costo se distribuye entre el número total de variables censadas (75), el costo aproximado de conocer sólo totales de población es de unos 60 mdp; por su parte, la adquisición de LIDAR involucra dos costos, uno fijo por traslado del sensor (por 21 mil dólares) más otro por cobertura (150 dólares/km², en promedio), que es más de 10 veces el costo de las imágenes multiespectrales (13 dólares/km²). Aunque el costo de traslado del sensor suele amortiguarse si se sobrepasa una cobertura mínima, es claro que un levantamiento de todo el territorio nacional resulta impráctica e innecesaria, sobre todo porque 72% de la población se encuentra en áreas urbanas que representan sólo 0.6% de éste (Grajales, 2011). Así, considerando una cobertura conservadora de 30 mil km² a nivel nacional (1.5% del territorio), el costo estimado del levantamiento LIDAR con las imágenes rondaría los 70 mdp lo que, evidentemente, es inviable, pues a esto habría que aumentar los costos asociados al procesamiento de los datos. En todo caso, el costo-beneficio de las adquisiciones de este tipo de datos debe verse en términos de la multiplicidad de usos que se les puede dar en ámbitos como el urbano, agrícola, forestal y ambiental. Más aún, es de esperase que, a medida que la tecnología se popularice, los costos de adquisición tiendan a bajar. En tanto eso ocurre, resulta útil evaluar los niveles de confiabilidad que se pueden alcanzar con estas metodologías.

Queda claro que para estimar la población ha de estimarse de forma adecuada la vivienda para reducir el margen de error en la estimación. Por su parte, las pruebas hechas mostraron que la estimación de viviendas a partir de datos de edificios resultó ser muy compleja. En este caso, se desarrollaron hasta 10 modelos, de los cuales resultaron mejores aquéllos que incorporaron un enfoque incremental, es decir, que requirieron información de edificios y viviendas tanto para una fecha previa como para la de la estimación. En estos casos, el nivel de error más bajo fue de 10% en términos relativos. No obstante, se debe destacar que las características de los datos alimentados en estos casos no fue similar para ambas fechas, pues para la primera la información de edificios se extrajo del catastro, mientras que para la segunda se sacó de datos de percepción remota. Presumiblemente, esto debió ser un factor para que el nivel de error de las estimaciones no resultara aún más bajo.

Otro factor fue, sin duda, la incapacidad de incorporar la información de uso de suelo en el caso incremental. Esto se infiere porque los modelos no incrementales que incorporaron la información de uso de suelo disponible en el catastro mostraron que ésta es de gran importancia para estimar las viviendas en áreas con uso de suelo fuertemente sectorizado, como en el caso de la delegación Cuauhtémoc. Previamente, se habían realizado pruebas para detectar edificios de viviendas a partir de sus características físicas, como tamaño y distribución (Silván-Cárdenas, Almazán-González y Couturier, 2014). Si bien los resultados fueron poco favorables, debido a que muchas edificaciones presentan uso de suelo mezclado, se intuye que aun con una detección perfecta de edificios de vivienda se presenta la dificultad de que la población se aloje en otros usos de suelo distinto al habitacional, lo cual hace que la relación área habitable-viviendas sea más errática. Por esta razón, en esta investigación se desarrollaron modelos que no consideran la información de uso de suelo, los cuales probaron ser útiles en ciertos casos, en específico, en áreas donde la mezcla de uso de suelo es más homogénea y donde el crecimiento en altura no es tan significativo, como en Milpa Alta. Para este caso, resultó suficiente emplear como indicador de viviendas el número de edificios con uso habitacional reportado en catastro (modelos V1 y V2) o el área habitable de todos los edificios, sin importar su uso de suelo (modelos V7 y V8).

Dos fenómenos que no fueron considerados al momento del desarrollo de los modelos y que, de manera eventual, podrían explicar parte del margen de error son el hacinamiento y la desocupación de la vivienda. El primero lo definió el INEGI para el Censo de Población y Vivienda 2010 como el “Porcentaje de viviendas con más de 2.5 ocupantes por dormitorio…” (INEGI, 2010). Para la Sociedad Hipotecaria Federal (SHF), este concepto implica la existencia de dos o más hogares por vivienda (SHF, 2012, p. 1). El fenómeno del hacinamiento, como indicador de marginalidad, supone el comprometer la privacidad de los habitantes de una vivienda, propiciando espacios no adecuados para el desarrollo de las actividades esenciales para las personas. Según el Consejo Nacional de Población (CONAPO), “Ninguna fuente de información (incluido el censo) proporciona datos sobre el tamaño del espacio físico y las dimensiones de los dormitorios y de la vivienda, para relacionarlas con el número de personas que los ocupan…” (CONAPO, 2011, p. 21), hecho que, por sí mismo, constituye un obstáculo para el correcto desarrollo de los modelos aquí planteados, en especial los basados en la relación entre el área habitable y el número de viviendas. Si la población está en función del número de viviendas, y las viviendas están en función del área habitable, deberíamos poder conocer el porcentaje del área habitable que se encuentra en condiciones de hacinamiento para diferenciarla de las demás, de tal modo que el modelo fuera diferenciado para zonas con mayor probabilidad de hacinamiento y para otras con un comportamiento constante en este indicador.

Tan sólo en el DF, hacia el 2011, se estimaba que alrededor de 35% del total de viviendas tenía algún grado de hacinamiento, provocado directamente por el fenómeno poblacional del desdoblamiento, que “…lleva a que donde antes vivía una pareja con uno o dos hijos, ahora también [lo hacen] nueras, yernos, nietos o abuelos…” (Llanos, 2012). A pesar de que estos datos son matizados por el CONAPO —según esta fuente, el DF presentaba 34.8% de viviendas con algún nivel de hacinamiento hacia el 2005, mientras que para el 2010 esta cifra se ubicó en 26.1% (2011: 21)—, lo cierto es que casi una de cada tres viviendas presenta esta situación y que al año, al menos 35 mil familias nuevas buscan satisfacer sus necesidades de vivienda y, cuando no son satisfechas, se integran a hogares ya formados (INVI, 2011).

En términos del modelo incremental, lo anterior podría significar que de un periodo a otro, las familias que se han desdoblado y no han ocupado o comprado una vivienda, estarían abonando al problema de la subestimación de la población que reside en una vivienda, problema reportado en las imágenes 7, 8 y 9.

De modo análogo, se plantea que el fenómeno del abandono o la desocupación de la vivienda podría ser un factor que esté influyendo en la sobrestimación de la población observada con anterioridad, al estimar un crecimiento poblacional derivado de un aumento de viviendas que, de facto, no están habitadas. Diversas fuentes consultadas (INEGI, 2010; Sánchez y Salazar, 2011) coinciden en que alrededor de 8% del total de viviendas en el DF se encuentra en esta situación, hecho que tampoco fue considerado en los modelos incrementales. A pesar de ser una de las tasas más bajas del país y de que siempre existirá en el mercado un porcentaje positivo de desocupación derivado de procesos y tiempos naturales del mercado inmobiliario (la absorción de la vivienda en el tejido urbano), puede ser un fenómeno que distorsione los resultados esperados.

Conclusiones

En este artículo hemos dado cuenta de diversos modelos que, de manera eventual, podrían ser utilizados para estimar de forma rápida un cambio en la cantidad de población en áreas pequeñas con base en información captada por sensores montados a bordo de plataformas aéreas y satelitales. La evidencia encontrada apunta a que es factible estimar la población en áreas pequeñas a partir del número de viviendas, el cual se puede inferir, a su vez y en ciertos casos, a partir de observaciones de percepción remota. Para determinar hasta qué punto es importante el estado de densificación del área donde se quiere estimar la población, se corrieron pruebas para tres delegaciones representativas de densidades alta, media y baja. Se encontró que es posible construir un modelo de estimación de población en términos de viviendas, cuyo desempeño es casi independiente de la densidad de población (modelo P5); en otras palabras, si el número de viviendas se pudiera determinar con mucha precisión, entonces es posible hacer una estimación de la población con un error relativo de no más de 5 por ciento.

No obstante, al estimar el número de viviendas con datos de percepción remota y del catastro, la cota superior del error de estimación de la población incrementó hasta 15 por ciento. Hay que considerar que este nivel de error se obtiene cuando se hace el ajuste en dos etapas: primero para estimar la población mediante datos de viviendas reales y luego para estimar las viviendas a partir del área habitable. Es de esperar que el error pueda ser menor si se hace un ajuste directo entre área habitable y población, esto a expensas de complicar la optimización de parámetros ya que se imposibilitaría la regresión lineal simple.

Al observar la distribución espacial de los errores de estimación de población a nivel de AGEB, se notó un agrupamiento de los tipos de errores (sobrestimación y subestimación) en función de la concentración de uso de suelo habitacional. Un análisis más a fondo de los errores de estimación sugiere que la distribución espacial de los mismos refleja la heterogeneidad espacial de fenómenos socioeconómicos, como el abandono y el hacinamiento, de tal forma que resulta necesario conocer la distribución espacial de dichas variables para poder reducir los errores de estimación poblacional obtenidos en esta investigación.

Fuentes

Arnal, S. Reglamento de Construcciones para el Distrito Federal. México, Trillas, 2005.

Azar, D.; R. Engstrom; J. Graesser y J. Comenetz. “Generation of fine-scale population layers using multi-resolution satellite imagery and geospatial data”, en: Remote Sensing of Environment. 130, 2013, pp. 219-232.

CONAPO. Índice de marginación por entidad federativa y municipio 2010. Consultado en bit.ly/4cQPF2K el 10 de septiembre de 2014.

Dobson, J. E.; E. A. Brlght; P. R. Coleman; R. C. Durfee y B. A. Worley. “LandScan: A Global Population Database for Estimating Populations at Risk”, en: Photogrammetric Engineering & Remote Sensing. 66(7), 2000, pp. 849-857.

Efroymson, M. “Multiple regression analysis”, en: Ralston, A. y H. Wilf (edits.). Mathematical Methods for Digital Computers. New York, Wiley, 1960, pp. 191-203.

González, L. y E. Torres. “Estimaciones de población en áreas menores en América Latina: Revisión de métodos utilizados”, en: Cavenaghi, S. Estimaciones y proyecciones de población en América Latina: desafíos de una agenda pendiente. Brasil, Asociación Latinoamericana de Población, 2012.

Grajales, S. G. Estado de las ciudades de México 2011. México, SEDESOL-Organización de las Naciones Unidas, 2011.

Harvey, J. T. “Estimating census district populations from satellite imagery: Some approaches and limitations”, en: International Journal of Remote Sensing. 23(10), 2002, pp. 2071-2095.

Iisaka, J. “Population estimation from Landsat imagery”, en: Remote Sensing of Environment. 12(4), 1982, pp. 259-272.

INEGI. XII Censo General de Población y Vivienda. Consultado en www.inegi.org.mx en el 2013.
_______ Censo de Población y Vivienda 2010. Consultado en www.inegi.org.mx en el 2013.

Instituto de Vivienda del Distrito Federal (INVI). Evaluación anual de resultados 2010-2011. Consultado en bit.ly/3y6m5am en el 2014.

Llanos, R. “Predomina hacinamiento en un tercio de viviendas de la capital”, en: La Jornada. 22 de febrero de 2012, p. 36.

Lu, D., Q. Weng y G. Li. “Residential population estimation using a remote sensing derived impervious surface approach”, en: International Journal of Remote Sensing. 27(16), 2006, pp. 3553-3570.

Lwin, K. K. y Y. Murayama. “Estimation of building population from LIDAR derived digital volume model”, en: Spatial analysis and modeling in geographical transformation process. 2011, pp. 87-98.

_______ “A GIS approach to estimation of building population for micro-spatial analysis”, en: Transactions in GIS. 13(4), 2009, pp. 401-414.

Nordbeck, S. “The law of allometric growth”, en: Michigan Inter-University Community of Mathematical Geographers, Discussion Paper 7. 1965.

_______ “Urban Allometric Growth”, en: Geografiska Annaler. Series B, Human Geography. 53(1), 1971, pp. 54-67.

Ordorica, M. y V. Ibarra. “Aplicación del filtro de Kalman para realizar estimaciones de población en áreas pequeñas”, en: Negrete Salas, M. E. et al. Entre fenómenos físicos y humanos. México, El Colegio de Mexico, 2002, pp. 201-217.

Qiu, F.; H. Sridharan y Y. Chun. “Spatial Autoregressive Model for Population Estimation at the Census Block Level Using LIDAR-derived Building Volume Information”, en: Cartography and Geographic Information Science. 37(3), 2010, pp. 239-257.

Salinas Arreortua, L. A. Transformaciones urbanas en el contexto neolibe-ral. Consultado en bit.ly/3Wi5jx7 el 9 de diciembre de 2014.

Sánchez, L. y C. Salazar. “Lo que dicen las viviendas deshabitadas sobre el censo de población 2010”, en: Coyuntura Demográfica, 1. Noviembre de 2011.

Sociedad Hipotecaria Federal (SHF). México: rezago habitacional, demanda de vivienda 2012 y bono demográfico. Consultado en bit.ly/3SeOeD2

Silván-Cárdenas, J. “A multiscale erosion operator for discriminating ground points in LIDAR point clouds”, en: Carrasco-Ochoa, J., J. Martínez-Trinidad, J. Salas-Rodriguez y G. S. Baja (eds.). Pattern Recognition. LNCS 7914. Querétaro, Springer Berlin Heidelberg, 2013, pp. 213-223.

Silván-Cárdenas, J. y L. Wang. “Extraction of Buildings Footprint from LIDAR Altimetry Data with the Hermite Transform”, en: Pattern Recognition-MCPR’11 Proceedings of the Third Mexican conference on Pattern recognition. 6718. Cancún, Mexico, Springer-Verlag Berlin Heidelberg, 2011, pp. 314-321.

_______ “Multiscale approach for ground filtering from Lidar altimetry measurements”, en: Weng, Q. Scale Issues in Remote Sensing. EE.UU., John Wiley y Sons, 2014, p. 18.

Silvan-Cárdenas, J., J. Almazán-González y S. Couturier. “Remote Identification of Housing Buildings with High-resolution Remote Sensing”, en: Lecture Notes in Computer Sciences. 8495. Cancún, Springer, 2014, pp. 380-390.

_______ “Remote Identification of Housing Buildings with High-resolution Remote Sensing”, en: Lecture Notes in Computer Sciences. 8495. Cancún, Springer, 2014, pp. 380-390.

Silván-Cárdenas, J., L. Wang, C. Wu, P. Rogerson, T. Feng y B. Kamphaus. “Assessing fine-spatial-resolution remote sensing for small-area population estimation”, en: International Journal of Remote Sensing. 31(21), 2010, pp. 5605-5634.

Sridharan, H. y F. Qiu. “A Spatially Disaggregated Areal Interpolation Model Using Light Detection and Ranging Derived Building Volumes”, en: Geographical Analysis. 45(3), 2013, pp. 238-258.

Sutton, P. “Census fom Heaven: an estimate of the global population using night-time satellite imagery”, en: International Journal and Remote Sesing. 22, 2000, pp. 3061-3079.

Sutton, P., D. Roberts, C. Elvidge y H. Melj. “A Comparison of Nighttime Satellite Imagery and Population Density for the Continental United States”, en: Photogrammetric Engineering & Remote Sensing. 63(11), 1997, pp. 1303-1313.

Wu, C. y A. T. Murray. “Population Estimation Using Landsat Enhanced Thematic Mapper Imagery”, en: Geographical Analysis. 39(1), 2007, pp. 26-43.

Yang, X., W. Yue y D. Gao. “Spatial improvement of human population distribution based on multi-sensor remote-sensing data: an input for exposure assessment”, en: International Journal of Remote Sensing. 35(15), 2013, pp. 5569-5583.

¹ Cabe anotar que los conteos no cuentan todo el universo, como en el caso de los censos.

² Área de la planta por el número de niveles.

³ Proceso de transformación urbana en el que la población original de un sector o barrio deteriorado es desplazada de manera progresiva por otra de un mayor nivel adquisitivo, a la vez que se renueva.

⁴ El art. 99 del Reglamento de Construcciones para el Distrito Federal (RCDF) vigente señala que la altura mínima para cualquier circulación en cualquier edificio no deberá de ser menor a 2.10 m de altura.

⁵ A pesar de que el art. 5.° del RCDF define una vivienda como un espacio habitable que contiene como mínimo 24 m², al final del mismo se establece que: “Se considerará vivienda mínima la que tenga, cuando menos, una pieza habitable y servicios completos de cocina y baño…”. El art. 9.° transitorio considera que una pieza habitable tiene como mínimo 7 m²; una cocina, 3 m²; y baño sin límites prestablecidos. Así, una vivienda mínima podría tener cuando menos 12 m²; sin embargo, es poco probable que tenga estas dimensiones dadas las necesidades adicionales espaciales, como patio de servicio/iluminación.

⁶ El modelo se refinó a tres segmentos a partir de un modelo propuesto de forma previa (Silván-Cárdenas, Almazán-González y Couturier, 2014).

⁷ Los requerimientos mínimos de altura se encuentran especificados en el capítulo 2 (Habitabilidad, accesibilidad y funcionamiento) de las Normas Técnicas Complementarias para el Proyecto Arquitectónico del RCDF (Arnal, 2005), destacándose que el rango mínimo para todos los tipos de edificaciones oscila entre 2.10 m y 3 m libres, sin contar los casos donde el director responsable de obra (DRO) determina la altura mínima. La altura máxima, exceptuando los casos donde interviene el DRO, es de 3.60 m para efecto de la contabilización del número de niveles. En caso de exceder esta altura, se tomará como equivalente a dos niveles construidos para efecto del conteo de elevadores y clasificación de usos y destinos.

⁸ A y B denotan los coeficientes de un modelo lineal genérico de la forma y = Ax + B. Éstos corresponden con los parámetros a y b de los modelos a través de transformaciones no lineales en los casos necesarios. Así, por ejemplo, mientras que para el modelo V1 A = a y B = b, para V2, A = a y B = log b, etcétera.