Incentivos, error de medición y estimación de la pobreza en México
Incentives, measurement error, and poverty estimation in Mexico
Alfonso Miranda*, a,c,d y Jaime Sainz Santamaría**,b,c
a División de Economía, Centro de Investigación y Docencia Económicas (CIDE); b División de Administración Pública, CIDE; c Programa de Estudios Longitudinales, Experimentos y Encuestas (PANEL); d Instituto para el Estudio del Trabajo (IZA), 53113 Bonn, Alemania.
*alfonso.miranda@cide.edu
**jaime.sainz@cide.edu
Nota: agradecemos a Cristina Álvarez Venzor por su excelente apoyo como asistente de investigación en la elaboración del presente documento; aquí se presenta la opinión de los autores y no necesariamente la del CIDE o del GTA; cualquier error u omisión es responsabilidad exclusiva de los autores.
Vol. 9 número especial – Epub Incentivos, error de medición… – Epub
|
En el 2015, el Instituto Nacional de Estadística y Geografía (INEGI) modificó la estrategia de recolección de datos del Módulo de Condiciones Socioeconómicas (MCS), la encuesta con la que se estiman los cambios de pobreza en México. La publicación de los resultados del MCS 2015 generó un intenso debate público debido a la discrepancia sustantiva en las tasas de pobreza 2014 y 2015, la cual no puede atribuirse exclusivamente a cambios verdaderos de la pobreza. Palabras clave: medición de la pobreza; error de medición; sistema de incentivos en encuestas; análisis longitudinal. |
In 2015 INEGI introduced changes to the fieldwork of the Socioeconomic Conditions Module (MCS by its Spanish acronym), which is the main survey that is used in Mexico to measure income and track changes in poverty. The publication of the results of the MCS 2015 sparked an intense public debate due to the stark discrepancy in the poverty rates 2014 and 2015, which cannot be exclusively attributed to true changes in poverty. Key words: poverty measurement; measurement error; incentive structure in surveys; longitudinal analysis. |
1. Introducción
El Módulo de Condiciones Socioeconómicas (MCS) de la Encuesta Nacional de Ingresos y Gastos de los Hogares (ENIGH) es la fuente primaria de información que el Consejo Nacional de Evaluación de la Política de Desarrollo Social (CONEVAL) utiliza para la medición de la pobreza multidimensional en México. En el 2015, el Instituto Nacional de Estadística y Geografía (INEGI) acordó con el CONEVAL que el levantamiento del MCS se realizara por primera vez como una encuesta independiente.
En julio del 2016, el INEGI dio a conocer los resultados del MCS 2015, y los niveles de ingreso que se registraron fueron mayores de lo esperado. De acuerdo con los datos publicados, el ingreso promedio de los hogares aumentó en 11.9% entre el 2014 y 2015. De forma importante, se detectó que el ingreso trimestral se incrementó considerablemente en cada decil de la distribución, que fue de 33% en el primer decil, 21.2% en el segundo, 17.7% en el tercero, 17% en el cuarto, 15.9% en el quinto, 15.5% en el sexto, 15% en el séptimo, 12.5% en el octavo, 10.1% en el noveno y 7.5% en el décimo.
Un análisis descriptivo revela que el tamaño promedio del hogar en el 2015 fue más pequeño de lo esperado por las proyecciones de población del Consejo Nacional de Población (CONAPO) y el ejercicio 2014 del MCS. Asimismo, el número de hogares aumentó 3.3%, muy por arriba de la proyección de 1.3% del CONAPO. En consecuencia, se sospecha que los hogares más pequeños están sobrerrepresentados. Además, entre el 2014 y 2015, el número de perceptores por hogar aumentó en 3.9% y el ingreso promedio por perceptor, en 7.7 por ciento. Claramente, el componente que más contribuye al incremento del ingreso es el aumento en el ingreso por perceptor.
El incremento del ingreso registrado en apenas un año resulta inverosímil y provoca cambios dramáticos en los cálculos de pobreza que elabora el CONEVAL. Desde un principio, el INEGI anunció que los cálculos de ingreso y pobreza basados en el MCS 2015 no eran comparables con las estadísticas generadas con el MCS de años anteriores. La falta de comparabilidad entre las series dificulta la tarea de medición de pobreza del CONEVAL, que se usa en las fórmulas para estipular el monto de recursos que recibe cada estado y municipio de la República Mexicana, con base en la Ley General de Desarrollo Social (que define las zonas de interés prioritarias para el gobierno federal) y la Ley de Coordinación Fiscal (que utiliza la medición para distribuir el Fondo de Aportaciones para la Infraestructura Social), entre otras leyes. En consecuencia, los cambios en la distribución del ingreso entre el MCS 2014 y MCS 2015 —y la pérdida de comparabilidad de la serie de índices de pobreza— tienen potencialmente consecuencias muy serias en la vida de millones de mexicanos.
Ante la relevancia del problema, el INEGI y el CONEVAL acordaron que se elaborara un ejercicio sintético que permita restablecer la comparabilidad de los datos del MCS 2014 y MCS 2015 de forma que el CONEVAL esté en condiciones de calcular un índice de pobreza 2015 que mantenga la continuidad en la serie de los índices de pobreza.
De acuerdo con el INEGI, el diseño del MCS es el mismo que en años anteriores. Se mantuvo la misma metodología en el 2015 que en los levantamientos anteriores: a) mismo diseño conceptual; b) mismo diseño estadístico; c) mismo operativo de campo (con cambios sutiles en apariencia, pero cuyos posibles impactos se discuten en este documento); d) mismo procesamiento y generación de datos; e) control muy similar; f) capacitación muy similar; y g) validación muy similar. Sin embargo, el INEGI reconoce que sí cambiaron algunos aspectos con el fin de mejorar la medición del ingreso. El ejercicio 2015 puso énfasis en captar los ingresos en forma adecuada y se detectaron, a partir del ejercicio 2014, áreas de oportunidad en la capacitación del personal que impactaban el registro de la información en temas como los siguientes: a) los ingresos de los negocios del hogar, b) las justificaciones de los hogares sin ingreso, c) las descripciones de los buscadores de trabajo y de personas no económicamente activas, d) las descripciones de a clave otros ingresos, e) las descripciones de otras prestaciones y e) el reporte del tipo de informante para los negocios del hogar.
El operativo de campo cambió, porque se agregó un nuevo apartado al Manual del entrevistador. En este artículo argumentamos que tal cambio potencialmente modificó la manera en que se conduce la entrevista. Entre otros aspectos, el apartado 10.2 instruye a los encuestadores como sigue:
- “Ten en mente la información previamente registrada en los diferentes cuestionarios, y si consideras que dicha información se contradice o requiere algún sondeo adicional, realiza el mismo y registra las observaciones necesarias que permitan avalar las diferentes situaciones”.
- “Cualquier información que te cause duda es mejor aclararla con el informante y realizar una observación al respecto”.
- “Cuando el informante te confirme que no tuvo ingreso alguno, realiza preguntas adicionales que te permitan identificar cómo se sostiene o cómo le hace para vivir, y en caso de que sea necesario, corrige la información previamente registrada o justifica la situación en las observaciones al final del cuestionario. De lo contrario, procederá un retorno a campo”.
- “Para los integrantes del hogar no ocupados, verifica que se cuente con información en alguno de los apartados de la Sección VII de dicho cuestionario; de no ser así, verifica esta situación con el informante y realiza las correcciones pertinentes”
Por otro lado, se definió el criterio C14, que establece condiciones bajo las cuales se debe volver a campo para verificar casos que generaran dudas sobre su veracidad. Su implementación involucró verificar en las oficinas centrales del INEGI la justificación de los entrevistadores para los hogares sin ingreso o con ingresos bajos. En ese ejercicio se evaluó, con base en la información del hogar, si ameritaba un retorno a campo. El criterio C14 se aplicó a 647 folios (0.98% de la muestra), de los cuales 215 (33.2%) derivaron en cambios de ingreso. De acuerdo con el INEGI, en ningún momento el personal operativo tuvo conocimiento del umbral para detonar el criterio.
Este artículo tiene una serie de notas conceptuales que pueden ser útiles para la discusión acerca de la medición de la pobreza en México, específicamente sobre la importancia del sistema de incentivos que enfrentan los encuestadores en los operativos de campo del INEGI y sobre la relevancia de expandir la estrategia de medición usando un enfoque longitudinal. La sección 2 contiene un diagnóstico de cuál es el posible origen de las diferencias entre el MCS 2014 y MCS 2015. Enseguida, la 3 muestra comentarios acerca de algunos de los ejercicios sintéticos que hasta el día de hoy ha realizado el INEGI. En la 4 se presentan algunos puntos e ideas de los cálculos de pobreza en México y reflexiona sobre cuál es el camino hacia adelante en el MCS y los cálculos de pobreza en México. Por último, se dan las conclusiones.
2. ¿Cuál es el origen de las diferencias entre el MCS 2014 y 2015?
En esta sección se presenta un modelo conceptual que muestra cuáles podrían ser las causas de las diferencias observadas entre los levantamientos 2014 y 2015 del Módulo.
Considere como punto de partida la ecuación de ingreso de Mincer (1958) para el 2014 y 2015:
y14= x14 β14+ u14 (1)
y15= x15 β15+ u15 (2)
donde y representa el ingreso, x es un vector 1 × K de características socioeconómicas (incluyendo la constante) y u es un error aleatorio. El vector (y, x) tiene una función de densidad conjunta f(y, x), la cual potencialmente cambia en el tiempo. En otras palabras, f(yt , xt ) define un proceso estocástico a través del tiempo con t={2014,2015}. En general, permitimos correlación del error con una o más variables explicativas E(u|x)≠0, de forma tal que el vector x es potencialmente endógeno. Suponga que el ingreso del 2014 fue medido por medio del MCS 2014 y el ingreso en el 2015, por el MCS 2015.
Para guiar la discusión, la gráfica 1 representa, de manera hipotética, la función de densidad conjunta del ingreso y las variables socioeconómicas x para los años 2014 y 2015. Note que (a) y (b) de esta gráfica no corresponden a los datos reales del MCS 2014 y 2015, son simplemente artefactos teóricos que nos ayudarán a discutir las aristas del problema que nos concierne. No se interprete, sin embargo, que las formas ilustradas de f(y14, x14) y f(y15, x15) son caprichosas. Por el contrario, el diseño tiene por objetivo resaltar características relevantes que exhiben los datos reales.
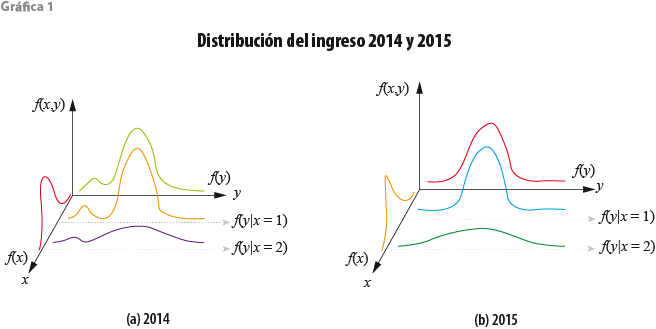
Sin pérdida de generalidad, se considera el caso donde el vector x contiene una sola variable x (además de la constante). En la gráfica se representan dos ejemplos posibles de la distribución marginal del ingreso: f(y) en la pared del fondo de la gráfica y la distribución marginal de la variable control f(x) en la pared del lado izquierdo. En el centro se representan ejemplos de la distribución condicional f(y|x). La función de densidad conjunta f(y, x) es la montaña de tres dimensiones que se forma con la unión de todas las funciones de densidad condicional a lo largo del rango de la x. Note que la densidad conjunta f(y, x) puede tener una forma muy irregular (gráfica 1.a). En consecuencia, como se muestra, la forma de la densidad condicional f(y|x) puede ser muy diferente para distintos valores de x. Eso involucra no solo la media condicional E(y|x), sino en general a todos los momentos condicionales m(y|x).
La pregunta central que nos ocupa es: ¿qué pudo cambiar entre el MCS 2014 y el MCS 2015?
En general, pudo cambiar:
- La densidad (distribución) marginal de las variables socioeconómicas f(x). Esto es, los hogares (personas) de México modificaron su perfil socioeconómico de forma importante entre el 2014 y 2015, promediando sobre la distribución de ingresos.
- La densidad (distribución) marginal del ingreso f(y). Esto es, los hogares (personas) de México recibieron un ingreso monetario significativamente diferente entre el 2014 y 2015, promediando sobre la distribución de sus características socioeconómicas.
- La densidad (distribución) conjunta del ingreso y las características socioeconómicas de la población f(y, x). Esto es, el ingreso que recibió el conjunto de personas definido por un perfil sociodemográfico cambió de manera importante entre el 2014 y 2015.1 Esto incluye:
a) Un cambio en los retornos monetarios a las características socioeconómicas en el mercado de trabajo. Esto es, un desplazamiento de la media condicional E(y|x)= xß debido a un cambio en los coeficientes ß.
b) Un cambio en el perfil sociodemográfico de la población (ver numeral 1) f(x).
c) Un cambio en la densidad (distribución) marginal del error f(u).
d) Un cambio en la densidad (distribución) condicional del error dadas las características sociodemográficas f(u|x).
Es difícil —sino imposible— pensar que el perfil sociodemográfico de los hogares en México cambió de forma importante entre el MCS 2014 y MCS 2015, ya que solo hay un año de diferencia entre los dos levantamientos. En un año, simplemente, no cambia la estructura de la población de manera importante y f(x) debería permanecer fija (a menos que el diseño de la muestra 2014 ó 2015 esté mal). Un argumento similar descarta que, en un periodo de 12 meses, existan cambios importantes en el retorno a las características demográficas de la población en el mercado de trabajo. En otras palabras, esperamos ß14= ß15. Entonces, si hay cambios en f(y, x) entre el MCS 2014 y MCS 2015, éstos seguro se deben a modificaciones en la distribución (densidad) condicional del error dadas las características socioeconómicas f(u|x).
Para aclarar el punto, la gráfica 2 superpone las dos densidades conjuntas f(u14, x14) y f(u15, x15), indicando en verde (líneas diagonales) la diferencia entre ambas gráficas. Aquí se dibuja la distribución conjunta f(u, x) tomando en cuenta que, si fijamos los coeficientes ß, la distribución de y está enteramente determinada por x y u. Note que los cambios entre el 2014 y 2015 están centrados en la parte izquierda de la distribución. En particular, en el 2014 (y en versiones previas del MCS) se observa una joroba en la cola izquierda que se forma porque una proporción importante de la población se niega a declarar ingresos, declara ingresos cero o declara ingresos muy pequeños, en un intento por ocultar información sensible o confidencial. Este comportamiento genera un error de medición que es particularmente acentuado en la parte izquierda de la distribución. Cabe aclarar que ésta no es una característica especial de los datos mexicanos, sino algo que se observa en la distribución del ingreso de todos los países del mundo. Existe una literatura amplia en el tema (ver, por ejemplo, Duncan y Hill, 1985; Rodgers y otros, 1993; Bound y Krueger, 1991; Bound y otros, 1994 y 2001; Hausman, 2001; Hyslop y Imbens, 2001; Biemer y otros, 2014; Kasprzyk, 2005; Gottschalk y Huynh, 2010; Nicoletti y otros, 2011; ChangHwan y Tamborini, 2014). Sabemos, también, que el deseo que las personas sienten por ocultar su ingreso es función del ingreso mismo y no solo de las características sociodemográficas. Así es, precisamente, cuando una persona tiene ingresos muy grandes o muy pequeños que tendrá mayores incentivos para ocultar o reportar de manera errónea su ingreso al encuestador del MCS (Duncan y Hill, 1985; Rodgers y otros, 1993; Bound y otros, 1994; Biemer y otros, 2014). Luego entonces, podemos concluir que el error de medición del ingreso es más grande en las colas de la distribución y que es función de las características socioeconómicas del hogar (persona), incluyendo el ingreso mismo.
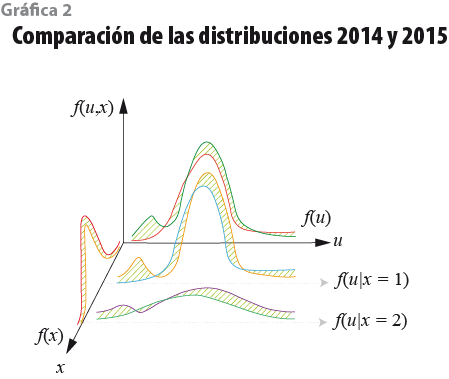Un ingrediente que complica aún más las cosas es que, potencialmente, los hogares (personas) que se niegan a declarar ingreso tienen características observables e inobservables de forma sistemática diferentes a los hogares que sí lo declaran. De hecho, con gran probabilidad, un dato faltante de ingreso no se genera como un acontecimiento casual, determinado completamente por el azar.
Rubín (1976) y Little y Rubín (2002) nos explican que los datos se pierden al azar, o son MAR (por sus siglas en inglés), cuando la probabilidad de tener un dato faltante depende de variables observadas, pero no de inobservadas. Por el contrario, cuando la probabilidad de perder un dato depende de variables inobservadas, se dice que los datos no se pierden al azar (o que son NMAR). Y si los datos que faltan son NMAR, la literatura muestra que surge un problema de sesgo de selección cuando el análisis se basa en la muestra observada y métodos convencionales de estimación (ver, por ejemplo, Heckman, 1979; Rubin, 1976; Little y Rubin, 2002). En el caso que nos ocupa, tenemos muy buenas razones para sospechar que los hogares más pobres y más ricos tienen mayor probabilidad de no declarar de manera correcta su ingreso (unos para evitar el estigma o por la dificultad de cuantificarlos, otros por razones de seguridad). Luego, seguramente, hay problemas de selección en la cola izquierda de la distribución del ingreso en el MCS debido a datos faltantes NMAR. El exceso de ingresos muy pequeños en el MCS se debe a un fenómeno muy similar al de datos faltantes. En la literatura esto se conoce como clumpling y es causado por un reporte erróneo (missreporting) del ingreso, en especial entre los autoempleados (Jenkins,1996; Parmeter, 2008; Hurst y otros, 2014).
Volvamos a nuestra pregunta: ¿qué cambió entre el 2014 y 2015? El INEGI ha explicado que, a diferencia de ejercicios anteriores, el MCS 2015 introdujo cambios en el operativo de campo con el objetivo de captar los ingresos de forma adecuada. En particular, se puso énfasis en validar con mucho más cuidado que en años anteriores la consistencia de la información de ingreso. El apartado 10.2 del Manual del entrevistador lo instruye a ser crítico e inquisitivo al momento de solicitar la información sobre ingreso. Ante cualquier duda sobre la consistencia de los datos, se pide al encuestador realizar preguntas adicionales para aclarar cómo el entrevistado se sostiene o qué hace para vivir. Si en función de las preguntas adicionales es necesario realizar modificaciones, debe corregir toda la información previamente registrada o justificar la situación en las observaciones al final del cuestionario. Más aún, ese apartado dice que si el entrevistador no justifica la situación en las observaciones de manera suficiente habría la posibilidad de un “retorno a campo”.
El criterio C14 estableció el umbral que se usó en la práctica para decidir qué folios requerían volver a campo para verificar la consistencia de la información sobre el ingreso. Además de dicho criterio, de acuerdo con el INEGI, se revisó en sus oficinas centrales la justificación de los entrevistadores para los hogares sin ingreso o con bajos ingresos y evaluó si ameritaba un retorno a campo. En la práctica, el retorno a campo se aplicó únicamente a 647 folios (0.98% de la muestra). Del total de folios verificados, solo en 215 casos (33%) se modificó el ingreso del hogar. De acuerdo con INEGI, en ningún momento el personal operativo en campo tuvo conocimiento del umbral para detonar el criterio.
Claramente, los cambios implementados al Manual del entrevistador y al entrenamiento tienen por efecto un cambio sustancial al operativo de campo del MCS 2015 respecto a lo que se hacía en el pasado. En años anteriores, el encuestador preguntaba ingreso y anotaba exactamente lo que la persona entrevistada le respondía. Si el informante se negaba a proporcionar datos de ingreso, el campo se dejaba sin llenar; si decía cero, se registraba un ingreso de cero. Si bien es cierto que en años anteriores el supervisor de campo verificaba la calidad y veracidad de la información, y que siempre había casos en los que se determinaba volver, en ejercicios anteriores el énfasis en el proceso de verificación de consistencia fue diferente, al menos en la capacitación del encuestador.
El MCS 2015 no solo introdujo un protocolo más estricto para verificar la consistencia y veracidad de la información del ingreso, sino que también dio, explícitamente, incentivos a los encuestadores para que hicieran bien su trabajo. En particular, se estableció en el Manual que el entrevistador tendría que “volver a campo” en caso de ser necesario.
Una de las lecciones más importantes de la teoría económica es que los incentivos importan. Esto es, modifican el comportamiento de los actores, y es posible que el apartado 10.2 modificara el contrato implícito entre el INEGI y el encuestador. En consecuencia, los incentivos y, probablemente, el comportamiento del entrevistador fueron diferentes para toda la muestra, no solo en los 647 casos que fueron finalmente sujetos a fiscalización. Para conocer la estructura de incentivos que enfrentó el encuestador, deben de conocerse —además de las indicaciones del Manual del entrevistador que se describen en este reporte— elementos clave del contrato implícito entre INEGI y quien recolectó los datos. En específico, es relevante saber si el gasto y esfuerzo que involucra regresar a campo son compartidos en alguna medida entre el INEGI y el encuestador: ¿el INEGI le paga por volver a campo, incluyendo viáticos?, ¿figura de alguna forma volver a campo en los indicadores de productividad del encuestador?
Los cambios en el operativo de campo del MCS 2015 (respecto a los ejercicios anteriores) afectaron de manera fundamental la distribución del error. El efecto se resintió en especial en la cola izquierda de la distribución, en los primeros deciles. La gráfica 2 ilustra las diferencias entre f(u14) y f(u15) en color amarillo. En la misma línea de investigación, la gráfica 3 muestra la diferencia del error du=u15-u14 a lo largo del rango de la x.
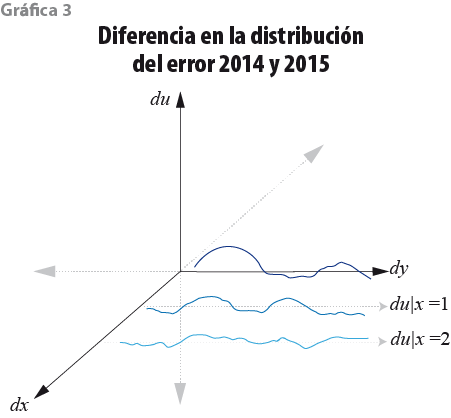Cabe aclarar que el problema no sería grave si los cambios en el protocolo de campo del 2015 solo afectan la distribución (densidad) marginal del error f(u), pero no la distribución condicional f(u|x). Esto ocurriría, por ejemplo, si las personas con baja educación reportaran su ingreso de forma errónea —o en el caso en que simplemente se negaran a reportar ingreso— con la misma frecuencia y en el mismo sentido y magnitud que aquéllas con alta educación. Bajo esas condiciones, el cambio en el error entre el 2014 y 2015 no es función de las variables socioeconómicas y, por lo tanto, es cero cuando se promedia sobre la distribución de las x. En consecuencia, una estrategia que calibra la distribución de las x del 2015 para que sea igual a la distribución de las x del 2014 debería restablecer de manera satisfactoria la distribución del ingreso. El problema es que, por razones que ya expusimos antes, lo más probable es que los cambios en el protocolo de campo afectaran la distribución del error dadas las variables control f(u|x). Eso hace que los cambios en el error de medición sean sistemáticos en diferentes áreas de la distribución de las x, es decir, que sean endógenos. En ese contexto, no es posible recuperar una distribución del ingreso en el 2015 que sea comparable con la del 2014, ya que el error es una variable inobservada.
Dado que el error u no es observable, ¿qué podemos hacer para recuperar una distribución del ingreso con base en el MCS 2015 que sea comparable con la distribución del ingreso del MCS 2014? Lo mejor sería implementar un experimento. Básicamente, la idea sería pedir a una muestra representativa de personas de la población que respondiera el cuestionario del MCS bajo las condiciones del protocolo de campo 2014 y bajo las condiciones del protocolo de campo 2015. El mismo conjunto de personas debe responder el cuestionario en ambas condiciones. Así sería posible inferir cuál es el cambio en el comportamiento que generan las diferencias en el protocolo de campo e investigar qué cambios se presentan en la distribución del error, dadas las variables socioeconómicas. Se deberán definir cuidadosamente el grupo control y el grupo de tratamiento. El experimento también debería de investigar en qué medida los cambios en el protocolo de campo afectan el comportamiento del entrevistador. Para ello, se deberán diseñar varios protocolos y definir de manera adecuada el grupo control y los grupos de tratamiento.
Existen otras alternativas que pueden lograr un ajuste, por naturaleza imperfectos, de la distribución del ingreso 2015. Aquí la clave es tratar de usar la densidad conjunta del ingreso y las variables socioeconómicas f(y, x) para generar un ejercicio sintético. Ajustar la distribución de las x no es suficiente, ya que fundamentalmente lo que cambió es la distribución del error dadas las x. De alguna forma se trata de restrablecer la distribución del error 2014 en la distribución del ingreso 2015. La clave es modelar, para grupos definidos por el vector de variables explicativas x, el ingreso en el 2015 dadas las x y el ingreso 2014. En otras palabras, requerimos modelar:
yg,15| xg , yg,14 ; g = 1,…,G (3)
donde g representa el índice de grupo. Esta estrategia explotaría la densidad conjunta f( yg,15, yg,14, xg), la cual contiene información sobre el error en el 2014. La información proviene de la probabilidad condicional de yg,15 dado (yg,14, xg).
P(yg,15| xg , yg,14 ); g = 1,…,G (4)
Se puede implementar una estrategia de regresión, una de apareamiento (matching) en x14 y x15 con donación de y14, o bien, una de múltiple imputación de las x15 en base x14 con donación de la y14.
El truco es usar la distribución conjunta de (yg,15, yg,14, xg) para restablecer la distribución del error en el 2015. Las estrategias sugeridas pueden ser empleadas para construir ponderadores de la muestra del 2015 que una vez aplicados a los datos —usando ponderación inversamente proporcional a la probabilidad (IPW)— recuperen una distribución del ingreso 2015 que es comparable con la distribución del ingreso 2014. Por supuesto, cualquiera de estos ejercicios serían imperfectos. La desventaja principal es que si se quiere medir los cambios en la pobreza entre el 2014 y 2015, el ejercicio sintético de alguna forma eliminará cambios reales en la distribución del ingreso (y el error) entre ambos años. Como mencionamos antes, es prácticamente imposible recuperar una distribución del ingreso 2015 que sea comparable con la del 2014 y que refleje cambios reales en la distribución del error no asociados a las modificaciones del protocolo de campo.
Una alternativa a la construcción de ponderadores para los datos del 2015 es crear, con base en las estrategias ya delineadas, una o varias bases de datos sintéticas que sustituyan los datos del 2015. Aquí la idea es muestrear repetidamente de la distribución conjunta de ( yg,15, yg,14, xg).
3. Comentarios a los ejercicios de ajuste (sintéticos) presentados por el INEGI
3.1. Ajuste demográfico por posestratificación
En el MCS 2015, el tamaño promedio del hogar es más pequeño de lo esperado de acuerdo con las proyecciones de población del CONAPO y el ejercicio 2014 del MCS. En consecuencia, se sospecha que los hogares más pequeños están sobrerrepresentados en la muestra. Además, el análisis descriptivo de la muestra 2015 indica que el número de perceptores por hogar y el ingreso promedio por perceptor aumentaron de forma importante. El componente que más contribuye al incremento total del ingreso es el aumento en el ingreso por perceptor.
La posestratificación corrige la sobrerrepresentación de los hogares pequeños haciendo uso de la Encuesta Intercensal 2015 para ajustar los ponderadores. La idea es que, una vez ponderada la muestra, se recupere una distribución de las variables socioeconómicas que sea comparable con los ejercicios anteriores.
Después de la posestratificación, el tamaño promedio de los hogares coincide con el del levantamiento del 2014. Antes de la ponderación, el MCS encontraba un crecimiento de 3.3% en el número de hogares entre el 2014 y 2015. Dicho crecimiento estaba en discordancia con las proyecciones de población del CONAPO. Después de la ponderación se tiene un crecimiento de solo 1.3%, muy cerca de la proyección del CONAPO de 1.29 por ciento.
El ejercicio de posestratificación logra reducir el ingreso corriente total (ICT) entre el 2014 y 2015. Resultados similares se reportan para el ingreso promedio por perceptor (IPP) y el número de perceptores por hogar (PH). Sin embargo, la corrección es pequeña.
3.1.1 Comentarios
Este sintético está basado en corregir la distribución de las variables socioeconómicas x con el fin de que f(x15) sea lo más similar posible a f(x14).
Dado que el objetivo principal del ejercicio es reparar la distribución de las variables socioeconómicas en el 2015 f(x15), y solo de forma indirecta el ingreso, es de esperar que el ejercicio tenga un impacto menor en la distribución marginal del ingreso. En consecuencia, el ejercicio hace poco por restablecer la comparabilidad entre el MCS 2014 y el MCS 2015.
Con el fin de evitar complicaciones en el uso de ponderadores, en la elaboración de la posestratificación se decidió construir un solo ponderador para toda la muestra. Desde el punto de vista de los autores, hay una ventana de oportunidad para mejorar la posestratificación elaborando un ponderador a nivel individual y uno a nivel hogar.2 Muchas encuestas en otras partes del mundo proveen ponderadores diferentes para hogares y para personas. Los usuarios pueden hacer uso correcto de los diferentes ponderadores si la base de datos contiene suficiente detalle sobre cómo emplearlos.
3.2. Ajuste demográfico por imputación
En la ENIGH, los hogares son visitados por siete días consecutivos, mientras que en el MCS 2015 la visita es de solo tres. En este contexto, la caída inesperada en el tamaño del hogar se puede deber a la omisión de personas, ya que en campo algunas veces el informante olvida reportar miembros del hogar en la primera visita. En la ENIGH, esos errores se corrigen en visitas posteriores, pero en el MCS 2015 hay menos tiempo para que el informante los corrija. La falta de muestra ENIGH exacerba el problema.
El ejercicio de imputación tiene como objetivo ajustar los factores de expansión del MCS 2015, como medio para restablecer la distribución correcta del tamaño del hogar en la muestra. Dicho objetivo se logra imputando los miembros del hogar perdidos en la muestra, para así dar menos peso a los hogares pequeños y más peso a los grandes.
Se propone corregir las características de los hogares del MCS por vía de un método de imputación Cold-Deck, que tiene por objetivo restituir a los miembros del hogar faltantes en el 2015; esta técnica define dos conjuntos de hogares: donadores y receptores. Los receptores son aquellos hogares donde se supone que desapareció uno o más miembros en el MCS 2015. Los donadores son aquellos que se parecen a los hogares receptores en todas sus características, excepto en el número de miembros. Esto es, se busca que la distribución de las variables socioeconómicas f(x) de donadores y receptores sea igual. Una vez apareados hogares donadores y receptores, se procede a transferir/imputar uno o más miembros del hogar donador al receptor. La técnica Hot-Deck usa la misma encuesta para buscar hogares donadores. Por el contrario, la Cold-Deck utiliza otras encuestas para buscar donadores. El proceso de imputación se realiza entidad por entidad. Para hacer la imputación, se usaron varias bases de datos: a) los MCS 2012, 2013, 2014 y 2015; b) la Encuesta Intercensal 2015; c) la Encuesta Nacional de Ocupación y Empleo (ENOE), tercer trimestre del 2015; y d) las proyecciones de los hogares en México y por entidades federativas 2010-2030.
Los resultados del ejercicio logran el objetivo de incrementar el tamaño del hogar de acuerdo con las tasas de variación implícitas calculadas a partir de las proyecciones de hogares y población del CONAPO. Los efectos del ejercicio sobre el ingreso y la pobreza son marginales. Se logra disminuir muy poco el monto del ingreso corriente y aumentar, también muy poco, al promedio de ingreso por hogar (debido a la disminución de los hogares) y la pobreza.
3.2.1 Comentarios
Este sintético está basado en corregir la distribución de las variables socioeconómicas x vía un ejercicio de imputación con el fin de que f(x15) sea lo más similar posible a f(x14).
En el ejercicio de imputación, el hogar donador es apareado al hogar receptor en función de características socioeconómicas x, pero no en función del ingreso. Éste queda fuera del vector de características de apareamiento.
Si el objetivo del ejercicio es corregir f(x), y solo indirectamente f(y), la corrección que se observa en la distribución del ingreso es pequeña y hace poco por restablecer la comparabilidad entre el MCS 2014 y el MCS 2015. Sin embargo, si los objetivos del ejercicio se extienden a lograr una buena corrección de f(y), entonces es posible mejorar el ejercicio explotando la distribución conjunta del ingreso y las características socioeconómicas f(y, x). Esto puede ayudar a restituir las características de la distribución del error 2014 en el 2015, dado los socioeconómicos. La discusión de la sección 2 abunda en este último punto. Para lograr dicho objetivo, es posible incluir el ingreso en el vector de características que se usan para implementar la imputación.
3.3. Propuesta para recuperar la comparabilidad del MCS 2015 usando máquinas de soporte vectorial
La técnica está basada en el uso de dos conjuntos de datos diferentes: 1) una base de datos de entrenamiento y 2) una base de datos de predicción. La primera contiene una serie de casos, en este caso hogares, con características x y clasificadas correctamente por deciles de ingreso, i.e. de acuerdo con la distribución f(y, x) del MCS de años anteriores. La de predicción son los datos del MCS 2015. Se busca clasificar a los hogares del MCS 2015 en deciles de ingreso con base en sus características socioeconómicas x y la experiencia de clasificación que la máquina de soporte vectorial (SVM, por sus siglas en inglés) obtiene de la base de datos de entrenamiento. Ésta incluyó los deciles (que tienen el rol de clases o categorías) y las covariables a nivel hogar de los MCS 2010, 2012 y 2014. SVM resuelve un problema de optimización que busca hiperplanos —que son función de las características socioeconómicas x— que identifican observaciones que pertenecen a una misma categoría, en este caso un decil. El problema de optimización minimiza el error de clasificación y asigna cada hogar del MCS 2015 a un decil pronosticado. Note que este procedimiento remueve, en un sentido limitado, el supuesto de que f(u|x) = f(u).
Con base en la clasificación pronosticada, se hace un ajuste en los factores de expansión para otorgarle mayor o menor peso a cada hogar, de acuerdo con el decil al que haya sido asignado. De esta forma, hogares con ingresos bajos tendrán un mayor peso.
El ajuste por Machine Learning logra que la variación del ICT entre el 2014 y 2015 a nivel nacional pase de 15.6 a 4.5 por ciento. En el primer decil, el ICT pasa de 38 a 11.2%, mientras que en el X pasa de 11.1 a 4.1 por ciento. En términos de pobreza, la población en pobreza pasa de ser 38.1 a 42.5%; la pobreza extrema, de 6.3 a 8.2%; y la moderada, de 31.8 a 34.3 por ciento.
3.3.1 Comentarios
El ejercicio de Machine Learning es el más prometedor. ¿Por qué SVM logra mejores resultados? Básicamente, porque se usa la distribución conjunta de las características socioeconómicas x y el ingreso y, f(y, x) para entrenar a la máquina de clasificación. En la sección 2 se recomienda, precisamente, hacer uso de la distribución conjunta para mejorar la predicción.
Abundemos un poco. La base de datos de entrenamiento tiene información de hogares con una serie de demográficos x que están clasificados en deciles de ingreso. Claramente, aquí hay información de la distribución conjunta f(y, x). De hecho, la base de datos de entrenamiento contiene una malla de 10 × K celdas, donde K es el número de celdas que genera la combinación de valores que puede tomar x; esa malla es una versión gruesa de la distribución conjunta f(y, x) —que no usa toda la información disponible sobre f(y, x), ya que los datos están clasificados únicamente en 10 celdas a pesar de que y es continua—; cuando SVM usa esa malla para entrenarse, el procedimiento explota, de forma limitada, la distribución conjunta para predecir el decil al que un hogar del MCS 2015 pertenece con base en su vector de características x.
Machine Learning está en el camino correcto. El sintético se puede mejorar si en vez de usar una malla con 10 celdas se usan 50 ó 100.
3.4. Armonización de los ingresos del MCS 2015 usando la ENOE como contrafactual
En ejercicios anteriores al 2015, el ingreso laboral promedio por hogar en el sexto decil del MCS y la ENOE es muy similar. En el 2015, esa coincidencia histórica se rompió debido a los cambios en el operativo de campo del MCS.
La continuidad de la ENOE y su similitud con el MCS para los levantamientos previos al 2015 permiten realizar un ejercicio sintético para restablecer la tendencia histórica que se rompió con el MCS 2015. El ejercicio consiste en un ajuste a nivel agregado que desplaza hacia atrás la distribución marginal del ingreso f(y) del MCS 2015 hasta lograr que el decil VI de la distribución marginal ajustada f*(y) coincida con el sexto decil de la ENOE 2015. Este método de ajuste, basado en el de método Máxima Verosimilitud, fue inicialmente sugerido por Bustos (2015). La desventaja del ejercicio sintético es que es necesario especificar una forma funcional para la distribución del ingreso. Después de considerar varias opciones, Ruiz y Romo (2017) eligieron una función de distribución Beta Generalizada (GB2). El procedimiento logra un ajuste macro, en el sentido de que modela la distribución del ingreso de los hogares a nivel agregado y no el ingreso de cada hogar de forma separada, para después agregar y estudiar las características de la distribución predicha. Nótese que aquí se modela la distribución marginal del ingreso f(y) y se ignora la información extra que contiene la distribución conjunta f(y, x).
Una vez que se tiene el ajuste macro de la distribución marginal f*(y), se procede a generar una base de microdatos consistente. En particular, para cada hogar h en la muestra del MCS se calcula la probabilidad de observar un ingreso menor o igual al reportado yh bajo la distribución marginal del ingreso en el MCS 2015 sin ajustar h = F(yh), donde F(•) es la función acumulada de probabilidad. Con 
h a la mano, se procede a usar la función inversa F-1 (•) para calcular el ingreso del hogar bajo la distribución ajustada 
.
En términos de resultados, el ejercicio logra que la variación entre el 2014 y 2015 del ICT pase de ser 15.6% a ser solo de 4.7 por ciento. Por otro lado, el ICT promedio por hogar, que presentaba una diferencia de 11.9% antes del ajuste, varía en 1.4% después del ejercicio sintético.
Los resultados agregados del ejercicio sintético son razonables, bajo el criterio de que parecen reconstruir la tendencia histórica. Sin embargo, cuando se analizan los deciles de ingreso, el sintético sigue obteniendo cifras insatisfactorias. Por ejemplo, el crecimiento del ICT entre el 2014 y 2015 en el decil I después del ajuste es aún de 13.4% (antes del ajuste era 38%). Y con excepción de los deciles IX y X, el crecimiento del ingreso entre el 2014 y 2015 es superior a 5% en todos los deciles. Claramente, un aumento del ingreso de los hogares en un solo año que resulta inverosímil dadas las condiciones macroeconómicas de México entre el 2014 y 2015.
3.4.1 Comentarios
Una versión modificada, pero basada en los mismos principios, de este ejercicio es lo que finalmente eligió el INEGI para construir el modelo estadístico 2015 —y 2016— para la compatibilidad del MCS-ENIGH. Por un lado, tiene la ventaja de que hace uso de la ENOE, la cual tiene registro del ingreso laboral, como fuente de información independiente. La ENOE es, probablemente, la segunda encuesta más importante levantada por el INEGI, donde se registra el ingreso laboral de los hogares y que tiene representatividad para los 32 estados de la República. Luego entonces, es intuitivo usar información de esta encuesta para ajustar el MCS, en especial porque en la ENOE 2015 no se observaron quiebres en la distribución del ingreso en el 2015 respecto a la tendencia histórica. Por otro lado, el sintético tiene la relativa ventaja de ser intuitivo y fácil de explicar. Sin embargo, desde nuestro punto de vista, tiene serias desventajas.
En primer lugar, el ejercicio no hace uso de toda la información disponible ya que, en lugar de explotar la riqueza de los microdatos del MCS y de la ENOE, se decide hacer un ajuste donde solo se modelan agregados macroeconómicos y se desestima la información que contiene la distribución conjunta f(y, x). No se explota ningún aspecto de la distribución conjunta f(y, x). Simplemente, se usa el sexto decil —o en el ejercicio final, la mediana del ingreso a nivel estatal reportado entre el segundo y el tercer trimestre de la encuesta— de la ENOE 2015 como pivote para desplazar y anclar la distribución marginal del ingreso f(y) del MCS 2015. En consecuencia: 1) la aproximación no aprovecha información relevante y 2) no tiene una clara justificación teórica, más allá de apelar al uso de una regularidad en las series de ingreso: históricamente, el sexto decil de la ENOE coincide con el sexto decil del Módulo de Condiciones Socioeconómicas.3
Hay una serie de preguntas obligadas: ¿por qué la ENOE y el MCS coinciden justo en el sexto decil?; si las dos encuestas miden ingreso laboral en la misma población, ¿no deberían coincidir a lo largo de toda la distribución?; ¿hay una razón teórica que explique por qué el punto de contacto es el sexto decil? Estas preguntas son difíciles de responder. Aquí lanzamos una hipótesis: posiblemente, la mayoría de las personas en el sexto decil son trabajadores del sector formal que reciben sus salarios por nómina, no tienen negocios ni actividades empresariales y pagan impuestos vía el sistema de retención automática del impuesto sobre la renta (ISR). En otras palabras, es precisamente en el sexto decil que se concentran los hogares con ingresos fáciles de medir y que tienen muy pocos incentivos a mentir sobre sus ingresos. Es allí, en el sexto decil, donde el error de medición es mínimo. Conforme nos movemos hacia las colas de la distribución del ingreso, el error de medición crece. En los extremos, la distribución del ingreso en el MCS y la ENOE se separan y no es fácil decir desde un punto de vista teórico cuál de los dos instrumentos es mejor.
Otro problema con el sintético por ajuste del ingreso laboral es que el ejercicio macro usa un solo pivote (o punto de anclaje). Claramente, el método es poco flexible, y sería mucho mejor hacer uso de varios puntos de anclaje para permitir un mejor ajuste. En apariencia, la única razón que impide usar varios puntos de anclaje es más práctica que teórica: la ENOE y el MCS solo coinciden en el sexto decil. A la luz de este punto, la ventaja inicial del sintético —es intuitivo y fácil de explicar— disminuye, ya que la simpleza se logra a partir de introducir supuestos difíciles de justificar y con la desventaja de quitar flexibilidad al modelo para adaptarse a los datos.4
Por último, el sintético tiene el problema de ser un método que modela agregados macro, que al ajustar solo la distribución marginal del ingreso f(y) —y no la distribución conjunta f(y, x)— rompe de manera implícita la relación entre el ingreso y las variables socioeconómicas x. Después, sin hacer explícitos los supuestos que justifican la validez del ejercicio, usa la función inversa F*-1 (•) y crea una base de microdatos sintética. Esto, efectivamente, equivale a crear una distribución conjunta artificial f*(y, x) que no tiene relación, a menos que se introduzcan supuestos muy restrictivos, con la distribución conjunta original . f(y, x),5 En la práctica, eso quiere decir que si el investigador usa la base de datos original del MCS 2015 para hacer análisis multivariado encontrará un conjunto de relaciones y coeficientes entre y y x muy diferentes a que si usa la base de microdatos sintética. En conclusión, con el ejercicio sintético la relación entre el ingreso y las variables socioeconómicas ha sido artificialmente modificada. El usuario debiera ser advertido explícitamente de evitar hacer análisis multivariado con la base de datos sintética.
4. Comentarios sobre los cálculos de pobreza en México y el camino hacia adelante
La problemática expuesta en el presente documento sugiere que es necesario reflexionar sobre la metodología y los datos que se usan hoy en día para la medición de pobreza en México, en especial si se quiere medir cómo cambia la pobreza a través del tiempo. Dicha reflexión permitirá identificar limitaciones de la actual metodología y trazar una ruta para mejorar los cálculos de la pobreza en el futuro.
Sabemos que, en general, la información proveniente de encuestas tiende a subestimar el ingreso (Nicoletti y otros, 2011). Hyslop y Townsend (2016) encontraron que los ingresos reportados, a través de una encuesta, por trabajadores de Nueva Zelanda son entre 2 y 4% menores que los reportados por datos administrativos. Los problemas de medición de la pobreza son aún más agudos en los países en desarrollo, principalmente en el caso de la población en los primeros deciles. Haughton y Khandker (2009) identificaron numerosas razones por las que los cálculos tienden a subestimar el ingreso de la población: la gente tiene problemas en recordar su ingreso, hay reticencias a declarar todas las fuentes de ingreso —en especial algunas que pueden provenir de fuentes ilegales o socialmente punibles—, es difícil calcular el valor de enseres que cambian de valor en el tiempo (ganado, por ejemplo). Haughton y Khandker (2009) señalan que la alternativa (medir consumo) puede complementar la información, pero no está exenta de errores: la gente subreporta consumo de alcohol o no reporta lujos o bienes ilícitos. En suma, las dificultades se traducen en tasas de pobreza sobreestimadas (Haughton y Khandker, 2009), a pesar de los esfuerzos del analista para tomar en cuenta el hecho de que la pobreza tiene múltiples dimensiones y que se manifiestan en una falta de acceso al consumo de bienes y servicios elementales (v.g. el enfoque de pobreza multidimensional del CONEVAL).
El problema de sobreestimación es más grave cuando se usan encuestas de corte transversal para estimar los cambios en los niveles de pobreza a través del tiempo (ver, por ejemplo, Gottschalk y Huynh, 2010; ChangHwan y Tamborini, 2014; Chesher y Schluter, 2002; Bound y otros, 1994; Bound y Krueger, 1991; Duncan y Hill, 1985). Veamos por qué haciendo uso de un ejemplo hipotético.
Al tomar una fotografía representativa de una población, v.g. la población del estado de Oaxaca, en un punto del tiempo t, una encuesta de corte transversal del estilo del Módulo de Condiciones Socioeconómicas permite determinar qué proporción de la población se encuentra por arriba y por abajo de la línea de pobreza en el punto t. Pensemos ahora en la dinámica temporal. Suponga, por ejemplo, que en t + 1 se repite el ejercicio y se levanta una segunda encuesta de corte transversal en Oaxaca. Considere que ambas encuestas son representativas de ese estado, pero que el conjunto de personas que entran a la muestra en el tiempo t es diferente del conjunto de personas que entran a la muestra en el tiempo t + 1, como sucede en las encuestas de corte transversal. En t + 1 podemos también medir la proporción de la población de Oaxaca que se encuentra por arriba y por abajo de la línea de pobreza. La tabla 1 presenta datos hipotéticos.
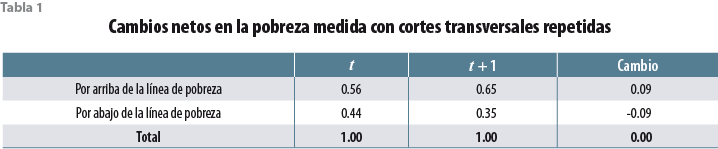
¿Podemos concluir a partir de la tabla 1 que disminuyó la pobreza en la población entre t y t + 1? Sí, pero eso no garantiza que las personas que eran pobres en t siguen siendo pobres en t + 1 ni que las que no eran pobres en t sigan sin ser pobres en t + 1. Todo lo que podemos saber son los flujos netos dentro y fuera de la pobreza. Para saber bien qué pasó entre t y t + 1, es necesario hacer uso de datos longitudinales (conocidos también como de panel) para calcular las tasas verdaderas de transición dentro y fuera de la pobreza (también conocidos como flujos brutos). A diferencia de un corte transversal, una encuesta longitudinal sigue al mismo conjunto de personas —que son una muestra representativa de la población— a través del tiempo.
Con la dimensión longitudinal se puede establecer con precisión si una determinada persona permanece o no bajo la línea de pobreza en los dos puntos en el tiempo. Con dicha información es posible calcular la matriz de transiciones.
Continuemos con nuestro caso hipotético. De la tabla 2 descubrimos que gran parte de las personas que caen en condición de pobreza no permanecen pobres por mucho tiempo. Ésos son los llamados pobres transicionales, compuestos por personas que en el momento de la entrevista no estaban empleados o que aceptaron temporalmente salarios bajos, pero que rápidamente se movieron hacia arriba. En el ejemplo, los pobres estructurales representan 15% de la población. Éste es el conjunto de personas que están en condición de pobreza de manera permanente. De forma similar, 36% de la población está permanentemente fuera de la pobreza. Claramente, como el ejemplo ilustra, la dimensión longitudinal de los datos es sustantiva para entender de forma profunda el fenómeno de la pobreza.
Note que la probabilidad de transición fuera de la pobreza es diferente de la probabilidad de transición dentro de la pobreza. De hecho, una persona pobre en el tiempo t tiene una probabilidad de 0.29 de salir de la pobreza en t + 1, mientras que una que no es pobre en t enfrenta una probabilidad de caer en pobreza de solo 0.20. La diferencia en las tasas de transición dentro y fuera de la pobreza explican la disminución neta en 9% en la proporción de pobres en la población entre t y t + 1.
En este punto cabe preguntar: ¿qué parte de la pobreza transicional es explicada por cambios en la distribución del error de medición entre t y t + 1?, ¿qué parte es generada por accidentes aleatorios que verdaderamente afectan el ingreso? Por ejemplo, desempleo temporal, enfermedad, eventos catastróficos (desastres naturales) o cambios en las condiciones macroeconómicas.
Si el análisis se hace exclusivamente con base en datos repetidos de corte transversal es imposible dar respuesta, ya que el analista no tiene idea de cómo cambia el error de medición entre el tiempo t y el tiempo t + 1. Con datos de diseño longitudinal es posible estimar modelos para la probabilidad de transición dentro y fuera de la pobreza y, con ello, limpiar (controlar) la influencia de la variación de los errores de medición del ingreso en los cálculos de pobreza. Es posible, además, comparar las diferentes dinámicas de transición entre estados (en este caso, pobre vs. no pobre) y cuáles son los efectos de las políticas públicas para combatir la pobreza y la inequidad.
En conclusión: la dimensión longitudinal no solo promete mayor riqueza de análisis (teórica y empírica) sino también permite controlar de mejor manera la influencia de las variaciones en la distribución del error de medición del ingreso. Es, desde nuestro punto de vista, la ruta hacia el futuro en el cálculo de la pobreza en México.
5. Conclusiones
En este documento se exploran las razones que explican la diferencias en la distribución del ingreso en la versión 2014 (y anteriores) y la del 2015 del Módulo de Condiciones Socioeconómicas.
La literatura sobre distribución de ingreso y su medición en encuestas nos proporciona elementos para sugerir que la versión 2014 (y anteriores) subestimaba los ingresos, tanto en la parte derecha como en la izquierda de la distribución. Se sabe que existe un error de medición que es generado por una combinación de problemas de datos truncados, datos censurados y datos faltantes. La literatura indica que el problema es más grave en la parte izquierda de la distribución. Para complicar las cosas, la probabilidad de no reporte, truncamiento y/o censura es función de las características de los hogares y las personas, incluyendo su ingreso. En otras palabras, la selección a un estado de observación, truncamiento y censura es informativa.
Dado que el error de medición depende de variables inobservables, es muy probable que se tenga un problema de sesgo de selección, el cual se manifiesta tanto en el número de casos con ingresos no declarados como en la frecuencia de valores pequeños en la cola izquierda y los montos parciales declarados en la cola derecha de la distribución. Éste es un problema común en todos los países del mundo y en todas las encuestas que miden ingreso. Este error de medición estaba presente en las versiones del MCS 2014 y anteriores. A partir de aquí se realizaban las mediciones de pobreza en México y, fundamentalmente, las estimaciones de la variación en la pobreza.
El protocolo de campo cambió en el 2015 con una clara intención de mejorar. Posiblemente lo logró, pues es probable que se mida mejor con la nueva estructura de incentivos. Sin embargo, al no prever que la modificación de incentivos podría alterar las estrategias y el nivel de esfuerzo de los encuestadores al recabar información, el INEGI no implementó un estudio —previo al despliegue de campo principal del MCS 2015— para estimar los posibles impactos del cambio metodológico. En consecuencia, no existe evidencia empírica que muestre efectivamente que se logró una mejora en la medición del ingreso. Un resultado imprevisto es que la nueva estrategia rompió la comparabilidad de la serie MCS 2015 con las estadísticas basadas en versiones anteriores del MCS.
Hoy por hoy, no sabemos cómo se compara la distribución del error en el 2014 con la distribución del error en el 2015. Conocer esas distribuciones y sus diferencias son la clave para lograr el mejor ajuste posible de la base de datos del 2015 y hacerla comparable con la del 2014.
Entender cómo cambió la distribución del error de medición es una tarea complicada. Es muy probable que no existen los datos necesarios para resolver el problema. Básicamente, se requiere saber cómo una persona (la misma persona) cambia su comportamiento cuando se enfrenta al protocolo 2015 en relación con el protocolo 2014. No solo hay que investigar el comportamiento del entrevistado, también hace falta investigar si el entrevistador modificó su comportamiento con el cambio de protocolo, en especial porque es posible que se hayan modificado sus incentivos para verificar la veracidad de la información.
La solución elegida para reconstruir la serie histórica fue la elaboración de un conjunto de ejercicios sintéticos, entre los cuales se escogió el enfoque basado en el ajuste del ingreso laboral con la ENOE. Cada uno de los ejercicios (incluido el que fue seleccionado para dar continuidad a la serie) tiene algunas ventajas (las cifras son más verosímiles, al menos en el agregado), pero presentan también problemas teóricos y empíricos que no pueden resolverse con los métodos propuestos.
En el presente documento se sugiere que la mejor forma de proceder es diseñar un experimento que permita esclarecer todas las incógnitas que hoy existen. Sin un experimento será difícil saber bien a bien qué pasó durante el levantamiento. En consecuencia, será difícil lograr un sintético bien fundamentado que satisfaga a todas las partes. El experimento supone diseñar una encuesta con diseño longitudinal que siga por algún tiempo al mismo conjunto de personas. Solo así se podrán definir bien grupos de control y de tratamiento, además de garantizar que exista soporte común. En principio se requiere someter un grupo de individuos solo al protocolo 2014, otro grupo únicamente al protocolo 2015 y un tercero a los dos protocolos. Algo similar se necesita diseñar del lado del encuestador. No se requiere representatividad a nivel estado o municipio para explorar las principales hipótesis, una encuesta longitudinal con representatividad nacional es suficiente. Esto es posible lograrlo con tamaños de muestra moderados.
Más sustancialmente, debemos decidir cómo proceder en el futuro. En particular, es necesario responder dos preguntas fundamentales: 1) ¿el instrumento anterior medía el ingreso de forma adecuada? y 2) ¿es posible medir de forma correcta —y atribuir una interpretación sustantiva— variaciones de la pobreza a través del tiempo con datos de corte transversal?
Desde el punto de vista de los autores, calcular variaciones en la pobreza a través del tiempo con base en datos de corte transversal es inadecuado. El estado del arte nos invita a hacer uso de datos longitudinales. Solo así podremos medir tasas de transición dentro y fuera de la pobreza a través del tiempo.
_____
6. Referencias
Biemer, P., S. Sudman, R. M. Groves, N. Mathiowetz y L. Lyberg. Measurement Errors inSurveys. Wiley Series in Probability and Statistics. Wiley, 2014.
Bound, J., C. Brown, G. Duncan y W. Rodgers. “Evidence on the Validity of CrossSectional and Longitudinal Labor Market Data”, en: Journal of Labor Economics, 12(3):345-368, 1994.
Bound, J., C. Brown y N. Mathiowetz. “Measurement error in survey data”, en: Heckman, J. and E. Leamer (editors). Handbook of Econometrics, volume 5 of Handbook of Econometrics, chapter 59, pages 3705-3843, 2001. Elsevier.
Bound, J. y A. B. Krueger. “The Extent of Measurement Error in Longitudinal Earnings Data: Do Two Wrongs Make a Right?”, en: Journal of Labor Economics, 9(1):1-24, 1991.
Bustos, A. “Estimation of the distribution of income from survey data, adjusting for compatibility with other sources”, en: Journal of the International Association for Official Statistics,31(4):565-577, 2015.
ChangHwan, K. y C. Tamborini. “Response error in earnings”. en: Sociological Methods & Research, 43(1):39-72, 2014.
Chesher, A. y C. Schluter. “Welfare measurement and measurement error, en: The Review of Economic Studies, 69(2):357-378, 2002
Duncan, G. J. y D. H. Hill. “An Investigation of the Extent and Consequences of Measurement Error in Labor-Economic Survey Data”, en: Journal of Labor Economics, 3(4):508-532, 1985
Gottschalk, P. y M. Huynh. “Are Earnings Inequality and Mobility Overstated? The Impact of Nonclassical Measurement Error”, en: The Review of Economics and Statistics, 92(2):302-315, 2010.
Haughton, J. y S. Khandker. Handbook on Poverty and Inequality. Number 11985 inWorld Bank Publications. The World Bank, 2009.
Hausman, J. “Mismeasured variables in econometric analysis: Problems from the right andproblems from the left”, en: The Journal of Economic Perspectives, 15(4):57-67, 2001.
Heckman, J. J. “Sample Selection Bias as a Specification Error”, en: Econometrica, 47(1):153-161, 1979.
Hurst, E., G. Li y B. Pugsley. “Are Household Surveys Like Tax Forms? Evidence from Income Underreporting of the Self-Employed”, en: The Review of Economics and Statistics,96(1):19-33, 2014.
Hyslop, D. y W. Townsend. “Earnings Dynamics and Measurement Error in Matched Survey and Administrative Data”, en: Working Papers 1618, MotuEconomicandPublicPolicyResearch. 2016.
Hyslop, D. R. y G. W. Imbens. “Bias from Classical and Other Forms of Measurement Error”, en: Journal of Business & Economic Statistics, 19(4):475-481, 2001.
Jenkins, S. “Recent trends in the uk income distribution: what happened and why?”, en: Oxford Review of Economic Policy, 12(1):29-46, 1996.
Kasprzyk, D. “Measurement error in household surveys: Sources and measurement”, en: Mathematica policy research reports, Mathematica Policy Research. 2005.
Little, R. J. A. y D. B. Rubin. Statistical anaysis with missing data. Hoboken, NJ, Wiley, 2002.
Mincer, J. “Investment in Human Capital and Personal Income Distribution”, en: Journal of Political Economy, 66:281-281, 1958.
Nicoletti, C., F. Peracchi y F. Foliano. “Estimating Income Poverty in the Presence ofMissing Data and Measurement Error”, en: Journal of Business & Economic Statistics, 29(1):61-72, 2011.
Parmeter, C. “The effect of measurement error on the estimated shape of the world distribution of income”, en: Economics Letters, 100(3):373-376, 2008.
Rodgers, W. L., C. Brown y G. J. Duncan. “Errors in survey reports of earnings, hours worked, and hourly wages”, en: Journal of the American Statistical Association, 88(424):1208-1218, 1993.
Rubin, D. B. “Inference and missing data”, en: Biometrika, 63:581-592, 1976.
Ruiz, J. y A. Romo. Armonización de los ingresos del MCS 2015 usando la ENOE como contrafactual. Mimeo. 2017.
_____
1 Por ejemplo, los hombres de 35 años de edad con estudios de secundaria que son empleados en la industria de la construcción de la Ciudad de México.
2 Por ejemplo, el Estudio Longitudinal de los Hogares en el Reino Unido proporciona un conjunto de ponderadores para hacer inferencia a nivel hogar y otro para hacer inferencia a nivel individuo (ver bit.ly/3LvpZfO). De forma similar, el Estudio Panel de la Dinámica del Ingreso de los EE.UU. proporciona un conjunto de ponderadores para hacer análisis de corte transversal y otro conjunto de ponderadores para hacer análisis longitudinal (ver bit.ly/3WrdqZk.
3 En el modelo estadístico para la compatibilidad —2015 y 2016— que finalmente publicó el INEGI se decidió no usar el sexto decil como ancla. En su lugar se usa la mediana del ingreso como ancla (en parte, en respuesta a los puntos débiles que aquí identificamos). Para agregar flexibilidad, se estimó el modelo para cada entidad federativa. Claramente, estimar el modelo entidad por entidad agrega flexibilidad al modelo. Sin embargo, dentro de cada entidad, se sigue usando un solo punto de anclaje. Por tanto, la ganancia en flexibilidad es pequeña.
4 En el ejercicio estadístico final se usa la mediana del ingreso en lugar de la media en el sexto decil. El punto débil persiste: ¿por qué usar solo un punto de anclaje? ¿Por qué usar como anclaje la mediana y no cualquier otro percentil?
5 En particular, se requiere que: 1) los datos sean MAR, 2) que los errores de medición nosean función del ingreso, 3) que al agregar los errores de medición promedien cero y 4) que exista suficiente continuidad y suavidad en f(y, x) para justificar el uso de la función inversa.
Ajuste del MCS 2015 por alineación de deciles
El gran escape
