Comparación de metodologías de imputación aplicadas a ingresos laborales de la ENOE

 

Comparison of Imputation Methodologies Applied to Labor Income of the ENOE

 

Benito Durán Romo*
* Instituto Nacional de Estadística y Geografía, benito.duran@inegi.org.mx
Nota: El autor agradece los valiosos comentarios de Gerardo Leyva Parra y la colaboración de Lilia Guadalupe Luna Ramírez para la elaboración de este documento.

 

Vol. 10, Núm. 3 – Epub                          Comparación de metodologías… – Epub

En las encuestas por muestreo aparece un problema muy común: la no respuesta; esta puede ser completa cuando no se consigue la entrevista o parcial cuando falta información de alguna sección o de tan solo una pregunta. La solución del primer caso no crea mayor conflicto, pues se resuelve ajustando los factores de expansión por no respuesta; sin embargo, el segundo presenta ciertas complicaciones. La Encuesta Nacional de Ocupación y Empleo del INEGI no está exenta de estas dificultades, ya que un porcentaje importante y creciente de personas ocupadas no responde a cierto número de preguntas pero, sobre todo, omite la declaración de sus ingresos por trabajo, presentando para este tema 6.7% de no respuesta en el primer trimestre del 2005 con un incremento permanente que alcanzó 16.8% en el cuarto del 2017. Las prácticas más frecuentes para tratar los casos con no respuesta parcial son la eliminación por lista o eliminación por pares, aunque ambas tienen sus inconvenientes. Otra forma de lidiar con datos faltantes en el análisis es mediante la imputación de estos utilizando metodologías de imputación simple o múltiple. Por lo anterior, el objetivo de este trabajo es mostrar los resultados de un ejercicio comparativo de algoritmos y metodologías de imputación de ingresos laborales de la Encuesta para ponerlas a consideración de los usuarios de esta y valorar su posible adopción como solución a los ingresos laborales faltantes, ejercicio que está basado en algunas medidas de desempeño y de los efectos que la imputación puede tener en el Índice de Tendencia Laboral de la Pobreza emitido por el Consejo Nacional de Evaluación de la Política de Desarrollo Social cada trimestre. Con esta investigación se encontraron resultados muy relevantes, como que los ingresos per cápita obtenidos por el Consejo están subestimados entre 16.7 y 23.5% en promedio, dependiendo de la metodología que se utilice, provocando así una disminución promedio entre 1 y 4% en el Índice. Palabras clave: no respuesta; no respuesta completa; no respuesta parcial; datos faltantes; imputación; imputación simple; imputación múltiple; Reglas de Rubin; eficiencia relativa; ENOE; ingresos laborales; ITLP.

A very common problem appears in sampling surveys: the “non-response”. This can be absolute when the interview is not taken or partial when information is missing from any section or from just one question. The resolution of the first case does not create greater conflict, as it is resolved by adjusting the expansion factors for non-response. However, the second one presents certain complications. The National Survey of Occupation and Employment of the INEGI is not exempt from these difficulties, since a significant and growing percentage of employed people do not answer a certain number of questions but, above all, omit the declaration of their income. On this subject, there was a 6.7% of non-response in the first quarter of 2005 with a permanent increase that reached 16.8% in the fourth quarter of 2017. The most frequent practices to treat cases with partial non-response are elimination by list or by pairs, although both have their drawbacks. Another way to deal with missing data in the analysis is by imputing them using single or multiple imputation methodologies. Therefore, the objective of this work is to show the results of a comparative exercise of algorithms and methodologies of imputation of labor income of the Survey to be put to the consideration of its users and to assess its possible adoption as a solution to the missing labor income , an exercise that is based on some performance measures and the effects that the imputation can have on the Labor Trend Index of Poverty issued by the National Council for the Evaluation of Social Development Policy every quarter. With this research, very relevant results were found, such as that the per capita income obtained by the Council is underestimated between 16.7 and 23.5% on average, depending on the methodology used, thus causing an average decrease between 1 and 4% in the Index. This study found very relevant results, such as the per capita income obtained by the CONEVAL are underestimated between 16.7 and 23.5% on average, depending on the methodology used, thus causing an average decrease between 1 and 4% in the ITLP. Key words: non-response; complete non-response; partial non-response; missing data; imputation; simple imputation; multiple imputation; Rubin’s Rules; relative efficiency; ENOE; labor income; ITLP.

Recibido: 24 de octubre de 2018.
Aceptado: 15 de febrero de 2019.

 

Introducción

En las encuestas por muestreo es común que se presenten problemas de no respuesta en dos sentidos: completa y parcial. La primera ocurre cuando no se logra la entrevista con la unidad de observación debido a que, por ejemplo, no pudo ser localizada por un problema de actualización del marco (una vivienda que en este aparece habitada y al momento de visitarla ya no lo está) o porque, aunque fue ubicada no fue posible contactarla, o bien, fue contactada pero sus ocupantes se negaron a proporcionar información. Por su parte, la parcial se da cuando aun lograda la entrevista no se dan datos para alguna sección o algunas preguntas de la entrevista, bien porque el informante no los tiene o, simplemente, no la(s) quiso contestar.

Al concentrarnos en el segundo caso, y en específico en las preguntas relacionadas con el ingreso de los individuos, este fenómeno se ha vuelto muy recurrente y se ha incrementado de manera persistente en México. Esta no respuesta en el reporte de ingresos puede deberse, principalmente, a que la información no es proporcionada por el perceptor directo, sino por un tercero que la conoce de forma parcial o que la desconoce en su totalidad; pero también puede ser causada por el miedo que provoca la creciente percepción de inseguridad en el país.

La Encuesta Nacional de Ocupación y Empleo (ENOE) no está exenta de este fenómeno, ya que reporta un porcentaje importante y al alza de personas ocupadas (como trabajadores subordinados remunerados, empleadores y trabajadores por cuenta propia) que no declaran sus ingresos por trabajo.

La variable de los ingresos laborales en la ENOE presentó 6.7% de no respuesta en el primer trimestre del 2005 y mantuvo un incremento permanente hasta alcanzar 16.8% durante el cuarto del 2017.

Pero el problema realmente no termina ahí, pues todo tipo de análisis realizados con información de esta encuesta y que involucra al ingreso por trabajo se llevan a cabo, la mayoría de las veces, eliminando las observaciones de los individuos con no respuesta en esta variable, o bien, considerándolos como cero ingreso, provocando que los resultados de esos análisis presenten sesgo.

La forma más común de resolver el problema de no respuesta completa de la unidad de observación es distribuyendo su factor de expansión en las unidades con respuesta del mismo conglomerado —el cual puede ser la Unidad Primaria de Muestreo (UPM)—, pero este procedimiento no es aplicable cuando falta respuesta de alguna pregunta durante la entrevista o, por lo menos, no es práctico: aquí lo recomendable sería imputar la respuesta.

La forma de proceder para preguntas con no respuesta parcial o datos faltantes rellenarlas usando metodologías de imputación simple o múltiple.

Aunque los procedimientos de imputación de datos faltantes han sido adoptados por un gran número de oficinas nacionales de estadística (ONE) desde hace varios años, el Instituto Nacional de Estadística y Geografía (INEGI), de México, no los ha implementado en ninguno de sus proyectos estadísticos en hogares.

Ante esto, el objetivo de este trabajo es mostrar los resultados de un ejercicio comparativo de algoritmos y metodologías de imputación de ingresos laborales de la ENOE para ponerlos a consideración de los usuarios de esta y valorar su posible adopción como solución a los ingresos laborales faltantes. Esta comparación se basa en algunas medidas de desempeño, pero también en la evaluación de los efectos que la imputación puede tener en el Índice de Tendencia Laboral de la Pobreza (ITLP) que emite el Consejo Nacional de Evaluación de la Política de Desarrollo Social (CONEVAL) cada trimestre y que es el uso más visible que se la ha dado a los ingresos laborales de la ENOE.

La presente investigación está organizada como sigue: en la primera sección se aborda una descripción general de la fuente de datos y sus problemas de no respuesta en los ingresos; algunas generalidades sobre imputación de datos faltantes y algunos casos de usos se tratan en la segunda; en la tercera se describen las metodologías de imputación a comparar; los resultados se muestran en la cuarta; y las conclusiones, en la quinta.

1. Los datos

La fuente que se usó para este trabajo fue la ENOE, como ya se había mencionado; esta proporciona amplia información sobre la fuerza laboral en México permitiendo su identificación y clasificación.

El objetivo general de la Encuesta es garantizar que se cuente con una base de información estadística acerca de las características ocupacionales de la población en el ámbito nacional, así como con la infraestructura sociodemográfica que permita profundizar en el análisis de los aspectos laborales.

La ENOE es un levantamiento continuo en hogares con una muestra de más de 120 mil viviendas organizadas en cinco paneles rotatorios que permanecen activos durante cinco trimestres consecutivos: se hace una visita a la vivienda por trimestre y se reemplaza cada panel de manera escalonada. Con ese tamaño de muestra se logra hacer inferencia estadística con desglose nacional, urbano y rural, por entidad federativa y 40 ciudades autorrepresentadas.

La Encuesta contempla un número importante de preguntas que permiten tanto determinar la condición de ocupación (ocupado, buscador de trabajo o no económicamente activo) de la población como conocer el contexto laboral de los ocupados en su empleo principal, así como las características de la unidad económica donde laboran y, también, algunos aspectos del empleo secundario, cuestiones relacionadas con antecedentes laborales, apoyos económicos, etcétera.

Dentro del ámbito laboral de los ocupados se incluyen dos preguntas para registrar el ingreso por trabajo que declare el informante: en la primera se indaga el monto y la frecuencia de pago; en caso de que no se proporcione la información, se hace la segunda, la cual presenta algunos intervalos de múltiplos de salarios mínimos, dando opción a que se seleccione cualquiera de estos.

Aun y con la presencia de las dos formas de proporcionar datos de los ingresos laborales por parte de los informantes, la ENOE ha registrado un incremento permanente en la no respuesta de estos. Como se puede observar en la gráfica 1a, esta comenzó con 6.7% en el primer trimestre del 2005 y alcanzó 17.2% en el tercero del 2017 (nivel más alto de la serie), volviendo a disminuir un poco (16.8%) en el cuarto de ese año.

En la misma gráfica se puede notar que la declaración en intervalos también se incrementó, aunque no en la misma magnitud que la no respuesta, al comenzar con 3.9% en el primer trimestre del 2005 y llegar a 10.7% en el cuarto del 2017.

Estos dos fenómenos han provocado que la declaración de ingreso en monto haya disminuido de forma constante al pasar de 89.4 a 72.5% entre el primer trimestre del 2005 y el cuarto del 2017, por lo que, si se va más allá y se considera a la declaración de ingresos en intervalos como no respuesta, entonces esta se incrementaría todavía más, teniendo 10.6% al inicio de la serie y alcanzando 27.5% en el cuarto trimestre del 2017, como se aprecia en la gráfica 1b.

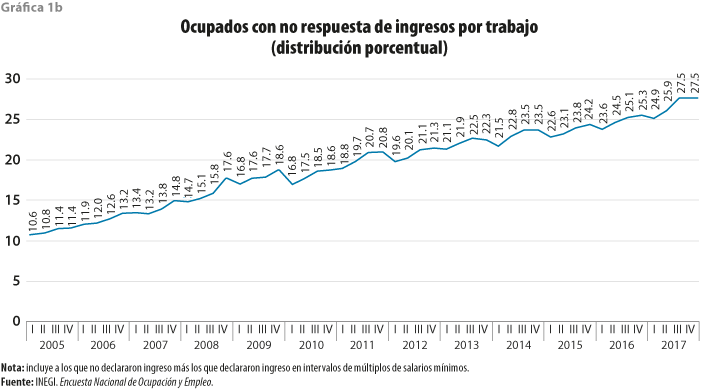
Y con esto último nos quedaremos para este trabajo, es decir, se considerará como no respuesta tanto a la falta de declaración de ingresos como a la declaración en intervalos de múltiplos de salarios mínimos. Este último caso es debido a que el tratamiento más común que se da es imputarle el punto medio del intervalo, lo cual es impreciso y arbitrario.

Cabe hacer mención de que estos dos fenómenos en su conjunto han estado creciendo 0.3% en promedio por trimestre, por lo que, de seguir esta tendencia, en 10 años estará rondando en 40 por ciento.

La falta de declaración de ingresos por trabajo puede deberse a múltiples factores, siendo uno de los más comunes cuando el informante adecuado no siempre es el informante directo, es decir, este es el que percibe en realidad los ingresos y es quien debería declararlos, pero por alguna razón no pudo ser entrevistado, y el adecuado es un integrante del hogar que, supuestamente, conoce la información del resto, sin embargo, esto no siempre ocurre así.

Otro factor que ha cobrado importancia en los últimos años es el constante incremento en la percepción de inseguridad en México, lo cual ha ocasionado que los informantes subdeclaren el monto del ingreso percibido, o bien, se nieguen a proporcionar el dato por miedo a ser víctimas de algún delito.

Aun y con este fuerte problema, se han hecho trabajos de análisis/generación de indicadores derivados de los ingresos laborales, y la manera de tratar los faltantes ha sido eliminando las observaciones, o bien, considerándolos como si no hubieran percibido ingresos (como cero ingreso), a pesar de saber que estas prácticas arrojan estimadores sesgados.

El Índice de Tendencia Laboral de la Pobreza es un caso donde se eliminaron las observaciones con ingresos faltantes. El Índice tiene como objetivo conocer la tendencia del poder adquisitivo del ingreso laboral, usando la ENOE como fuente de información.

Con lo expuesto anteriormente, es evidente que la ENOE tiene un problema importante de ingresos faltantes; con esto en mente, el presente ejercicio propone la alternativa de rellenarlos con datos imputados, por lo que se probarán diversos algoritmos/metodologías para llevarlo a cabo.

Una vez imputados los ingresos faltantes se realizará un ejercicio comparativo de esos algoritmos/metodologías en dos etapas, la primera a través de un conjunto de medidas de desempeño (error estándar, R², raíz del error cuadrático medio y el error medio absoluto) y la segunda usando el propio ITLP y algunos indicadores derivados de este.

La imputación de ingresos faltantes en la ENOE es una opción aceptable para solucionar este problema, pero, de seguir al alza la falta de declaración de ingresos en esta encuesta, en el futuro serán más las observaciones con datos imputados que con observados, por lo que es imperativo tomar las medidas necesarias en el operativo de campo para revertir esa tendencia.

2. Imputación de ingresos: conceptos y casos de uso

Las prácticas más comunes para llevar a cabo análisis con datos faltantes son la eliminación por lista (listwise deletion) y por pares (pairwise deletion). La primera, también llamada análisis de casos completos, elimina todas las observaciones que tengan por lo menos una variable con datos faltantes. En la segunda, denominada asimismo selección por variable o análisis de casos disponibles, solo descarta aquellas que presentan datos faltantes en la variable involucrada en el análisis.

Ambas tienen sus inconvenientes, por ejemplo, la eliminación por lista requiere que el mecanismo de datos faltantes sea MCAR¹,como lo mencionan Peugh y Enders (2004), ya que de ser MAR se generan estimadores sesgados, además de que la muestra puede reducirse lo suficiente como para producir estimadores poco confiables. En la que se hace por pares, también indican que la comparabilidad dentro de un estudio es problemática debido a las diferencias que pueden resultar en el tamaño de los subconjuntos de datos, además de requerir el supuesto de MCAR para producir estimadores insesgados.

Una alternativa a la eliminación de observaciones con datos faltantes en análisis es la imputación de éstos.

En Durán (2018) menciono que con la imputación se asigna un valor a una variable con no respuesta para que el cuestionario pase el proceso de validación en la entrada de datos y que la imputación puede ser una buena solución al trabajar con datos incompletos o faltantes (por no respuesta), pero que el procedimiento debe hacerse con el mayor de los cuidados porque, de no hacerlo, los datos completos pueden acabar muy sesgados y no mostrar la realidad que se pretende descubrir.

Para llevar a cabo este procedimiento, se pueden usar métodos de imputación simple, o bien, múltiple.

Imputación simple

En esta se asigna un solo valor a la variable con datos faltantes en cada una de las observaciones, dando como resultado un solo conjunto de datos completo.

El método tiene dos importantes características según Rubin (1987): la primera es que se pueden usar los métodos estándar de análisis de datos completos en el conjunto de datos imputado y la segunda es que cuando el conjunto de datos es de uso público, las imputaciones deben ser llevadas a cabo por el productor de los datos para que de esta forma sea incorporado su conocimiento sobre los mismos; pero Rubin también enumera dos desventajas: el valor imputado no refleja la variabilidad del muestreo sobre el valor real ni la incertidumbre que adicionan los datos faltantes.

La imputación basada en modelos (asignando una media, una mediana o el resultado de una regresión) y las técnicas Deck (Hot Deck y Cold Deck) son metodologías usadas en la imputación simple.

Imputación múltiple

Siguiendo el pensamiento de este mismo autor, esta conserva las virtudes de la simple, pero también corrige sus fallas, es decir, pueden usarse los métodos estándar de análisis de datos completos e incorporar el conocimiento del productor de los datos, el cual se ve reflejado en la incertidumbre sobre cuál dato imputar.

Con imputación múltiple se asignan m valores a la variable con datos perdidos para cada observación, dando como resultado m conjuntos de datos completos, es decir, se producen varios conjuntos de datos imputados (digamos m) donde cada uno de ellos contiene un valor imputado diferente para cada dato faltante. Se realiza el análisis por separado para los m conjuntos de datos y el valor del estimador será el promedio de los resultados de esos análisis, por ejemplo, el estimador del total será el promedio de los totales de los m conjuntos de datos, la media estará dada por el promedio de las medias de los m conjuntos de datos y así con otros estimadores. El cálculo de los errores estándar estará sujeto a las Reglas de Rubin (1987).²

Según Alisson (2012), hay dos razones por las que se requiere más de un conjunto de datos imputados: la primera se refiere a que, con un solo conjunto de datos, los estimadores serán altamente ineficientes debido a que tendrá más variabilidad de la necesaria, al promediar los resultados sobre varios conjuntos de datos esta se reduce; la segunda es que la variabilidad de las estimaciones en diversos conjuntos de datos proporciona la información necesaria para que los errores estándar reflejen con precisión la incertidumbre sobre los valores faltantes. También, menciona que estas dos razones tienen implicaciones en el número de imputaciones a efectuar.

Dado esto, Rubín (1987) introduce el término Eficiencia Relativa (ER) de los estimadores, la cual está dada por:

medida en unidades de desviaciones estándar y donde es la fracción de información faltante (algunos autores la refieren como la proporción de observaciones con datos faltantes) y m es el número de imputaciones.

Para entender de qué se está hablando, revisemos el cuadro 1, donde se observa la ER como porcentaje, que resulta de aplicar la fórmula anterior usando un número finito de imputaciones y cierta proporción de fracción de información faltante. Al usar como ejemplo la ENOE del cuarto trimestre del 2017 que alcanzó 27.5% de ingresos faltantes (casi 30%), se requieren 10 datos imputados para lograr una ER de 98.5%, es decir, con 30% de ingresos faltantes son suficientes 10 imputaciones para obtener estimadores 98.5% tan eficientes como los que se obtendrían con un número infinito de imputaciones. Es por esto que la mayoría de los expertos proponen que entre cinco y 10 imputaciones son suficientes para obtener estimadores eficientes.

Casos de uso

Algunas ONE usan, con frecuencia, los métodos de imputación simple para corregir los problemas de datos faltantes; por ejemplo, Statistics Canada usa la metodología Hot Deck para imputar en la Encuesta de la Fuerza Laboral (LFS, por sus siglas en inglés) y el Buró de Censos de Estados Unidos de América la utiliza en la Encuesta de Población Actual (CPS, por sus siglas en inglés) y en la Encuesta de Ingresos y Participación en el Programa (SIPP, por sus siglas en inglés).

En la Encuesta de Panel de Hogares Británica (BHPS, por sus siglas en inglés), Hot Deck se emplea en variables con poca presencia de valores como ingresos provenientes de inversiones o ahorros. En los casos donde la frecuencia de valores es alta se utiliza el método de pareamiento por medias predictivas. Al aplicar estos dos métodos pueden introducirse sesgos en las tasas de cambio de los valores entre rondas de levantamiento. Para evitarlo, se hace una imputación de rondas cruzadas, de tal forma que al seleccionar a la observación del donador no solo se escoge aquel con características similares al receptor, sino con valores similares obtenidos de las otras rondas de levantamiento (University of Essex, 2018).

Un caso interesante de imputación múltiple de ingreso es el que se realiza en la Encuesta de Gastos del Consumidor (CE, por sus siglas en inglés) recolectada por el Buró de Censos para el Buró de Estadísticas del Trabajo del Departamento del Trabajo de Estados Unidos de América, operativo que provee datos sobre gastos, ingresos y características demográficas de los consumidores estadounidenses.

De acuerdo con Paulin et al. (2006), el proceso de imputación múltiple en la CE comenzó en el 2004 con el fin de rellenar los huecos causados por no respuesta, logrando preservar la media de todas las fuentes de ingreso e incluso incorporar al cálculo de la varianza la incertidumbre causada por la imputación. Este proceso se lleva a cabo por medio de una regresión, donde los coeficientes obtenidos son distorsionados cada vez agregando ruido, los cuales son usados para estimar los datos faltantes (cinco estimaciones diferentes). Una vez estimados los datos, estos también son distorsionados agregándoles ruido con el fin de dar variabilidad a los resultados.

También, mencionan cómo obtener estimadores a partir de los datos imputados, pero enfatizando que las medidas de precisión de esos estimadores deben ser generadas tomando en cuenta las Reglas de Rubin (1987) usando los datos de las cinco estimaciones.

Cabe hacer mención que el Buró de Estadísticas del Trabajo pone a disposición del público en general los microdatos de la CE, los cuales incluyen los resultados de la imputación múltiple de las diferentes fuentes de ingreso y del ingreso total.

Otro caso para tomarse en cuenta es el presentado por Starick (2005), donde hace un análisis comparativo de metodologías de imputación aplicadas a los ingresos de la Encuesta sobre la Dinámica de los Hogares, los Ingresos y el Trabajo en Australia (HILDA, por sus siglas en inglés), la cual es una encuesta longitudinal que pone especial atención en la información de las viviendas y los hogares, además del trabajo e ingreso de los individuos.

Starick menciona que, aunque las metodologías de imputación para estudios transversales pueden ser una muy buena opción, tienen una desventaja: pueden introducir distorsiones en la tendencia de las estimaciones entre rondas de levantamiento. Ante esto, presenta la comparación de tres métodos de imputación para encuestas longitudinales: de regresión del vecino más cercano, Little and Su y Little and Su extendido.

En el primero se usa un paquete estadístico para construir los modelos de regresión que dependen de las rondas en que se observaron datos utilizando los valores predichos para buscar el vecino que tenga el valor más cercano al dato observado.

El segundo es un método de imputación simple para estudios longitudinales en variables continuas, el cual involucra información sobre la tendencia de los datos a través del tiempo y el dato de cada observación, de tal manera que el valor imputado está formado por los efectos de columna (que representa los cambios en la media a través del tiempo) y renglón (que es el nivel de la observación corregida por el de columna), además de un componente aleatorio como residual (calculado a partir de un valor observado cercano al de renglón), es decir:

imputación = efecto columna * efecto renglón* residual

Los efectos de este método (para mayores detalles sobre este, ver Eurostat, 2014) se calculan con base en todos los datos observados en cada ronda de levantamiento.

En Little and Su extendido se usa el mismo procedimiento anterior, salvo que los efectos se calculan con base en los datos observados de receptores y donadores con características similares.

Starick basa la comparación en algunos criterios que son evaluados con sus respectivas métricas, diferentes a las que aquí se presentan. De acuerdo con los resultados de esos criterios, ella recomienda el uso del Little and Su, pero haciéndole mejoras cada vez.

En México se han hecho esfuerzos para subsanar el problema de ingresos laborales faltantes en la ENOE llevando a cabo algunos ejercicios de imputación, pero todos ellos han tenido fines de investigación, por ejemplo, Campos-Vázquez (2013) imputó ingresos a la ENOE (del 2005 al 2012) usando cuatro técnicas: pareamiento por puntajes de propensión, Hot Deck, imputación en la mediana de un grupo más ruido y pareamiento por promedios predictivos, esto con el objetivo de medir la pobreza laboral y compararla con las mediciones del CONEVAL; en ese estudio se encontró que la pobreza laboral es menor entre 6 y 7% a la reportada por el Consejo.

También, Rodríguez y López (2015) imputan ingresos faltantes a la ENOE para después analizar las diferencias en pobreza laboral y el posible sesgo en estimaciones de capital humano cuando se ignoran dichas observaciones. Las técnicas que usaron son Hot Deck aleatorio y Hot Deck con función de distancia utilizando características observables demográficas de cada individuo y de su hogar para encontrar el donante. Ellos encontraron que, al no considerar las observaciones con ingresos faltantes, la pobreza laboral está sobrestimada y que los retornos a la educación serían alrededor de medio punto porcentual más bajos si se contempla el conjunto de datos completo (con imputados) y el sesgo no sería significativo.

Los anteriores son ejemplos del tratamiento alternativo que se puede hacer a los datos faltantes en las encuestas en hogares con el fin de disminuir al mínimo posible el sesgo al generar resultados a partir de ellas. Por ello, el presente trabajo es un ejercicio comparativo de metodologías de imputación de ingresos laborales de la ENOE para que usuarios de esta lo consideren, pero lo deseable es que el INEGI es quien deba proporcionar la solución a esta problemática a través de sus áreas sustantivas, adoptando la imputación como parte de sus actividades de procesamiento y, al hacerlo, el Instituto incorporaría el conocimiento de sus propios datos a ese procedimiento, que es una de las características que enumera Rubín (1987).

Cabe destacar que, aunque la ENOE es una encuesta de panel rotatorio (con cinco rondas de levantamiento cada panel), para esta investigación se le da el tratamiento de encuesta transversal, por lo que solo son comparadas metodologías de imputación para eventos transversales, dejando la comparativa para datos longitudinales para estudios futuros.

3. Metodologías de imputación a comparar

En este ejercicio se aplicaron la simple y la múltiple cuidando que el(los) valor(es) a imputar fuera(n) estimado(s) a partir de un conjunto de variables que pudieran explicar los ingresos laborales de los individuos.

Aunque la ENOE incluye un conjunto importante de variables, solo algunas aplican a las personas ocupadas y de estas se buscaron aquellas que tuvieran hasta 10 categorías y que todos los códigos presentaran un número importante de ocurrencias debido a las restricciones que imponían los algoritmos. De esta forma, se buscó que todas las metodologías se compararan bajo las mismas condiciones y restricciones. Además, se descartaron todas las variables continuas debido a que dificultaban el pareamiento en Hot Deck.

De esta manera, las variables seleccionadas fueron:

• Estrato sociodemográfico (cuatro categorías).
• Sexo.
• Edad (seis categorías) [eda7c].
• Nivel de instrucción (cuatro categorías) [niv_ins].
• Posición en la ocupación (tres categorías) [pos_ocu].
• Ocupación (10 categorías) [c_ocu11c].
• Rama de actividad (cinco categorías) [rama].
• Tipo de unidad económica (tres categorías) [tue1].
• Duración de la jornada laboral (cinco categorías) [dur_est].

Dado que todas las variables explicativas son categóricas, se descartaron aquellas metodologías que, para su funcionamiento, requieren solo variables continuas y las que imputan a partir de un donante y que usan una medida de distancia para encontrarlo, o bien, aquellas otras basadas en Análisis de Componentes Principales (ACP).

Cabe hacer mención de que la mayoría de estas variables incluyen códigos para No especificado, No sabe o No contestó, por lo que debieron considerarse como datos perdidos y codificados como NA (Not Available, que es como se identifica un dato perdido en R). También, la variable de ingresos laborales (ingocup) con valor 0 fue codificada con NA.

Además, para este trabajo solo se tomaron en cuenta a los individuos de 15 y más años de edad que reportaron estar ocupados y con códigos en la variable pos_ocu: 1) trabajadores subordinados y remunerados, 2) empleadores y 3) trabajadores por cuenta propia, excluyendo a 4) trabajadores sin pago.

Por otro lado, en la actualidad, experimentar con metodologías de imputación no es tan complicado. Algunos paquetes estadísticos (como Stata, SPSS y SAS) ya traen incorporadas estas funcionalidades, la desventaja es que son piezas de software que representan costos monetarios altos y no incluyen gran variedad de opciones metodológicas; sin embargo, existe R, que es totalmente gratuito y sí tiene un número importante de algoritmos con variedad de metodologías de imputación.

Entonces, tomando como software estadístico base a R, se experimentó con un número importante de algoritmos/metodologías, además de incluir dos algoritmos propios, que implementan la metodología Hot Deck aleatorio y la de bosques aleatorios en dos etapas, y desarrollados también en R, para al final trabajar con los siguientes algoritmos:

• Hot Deck
• Multivariate Imputation by Chained Equations (MICE).
• Amelia II.
• missForest.
• Hmisc.
• Mi.
• Rf2e

Otros fueron descartados, ya sea porque no convergieron, o bien, por el exceso de recursos que requieren para funcionar.

Todos los algoritmos, con excepción de Hot Deck aleatorio, imputan todas las variables especificadas en el modelo, pero en este ejercicio solo se reportan los resultados en el ingreso laboral de los individuos.

Las metodologías de imputación aplicadas se basan en el supuesto de que el mecanismo de datos faltantes de ingresos laborales es MAR,³ pudiéndose comprobar mediante un modelo de regresión logística donde la variable dependiente es binomial con valor 0 cuando no hay dato faltante y 1 cuando sí lo hay, y como covariables las enlistadas con anterioridad.

A continuación, se describen cada una de las metodologías usadas por algoritmo.

Hot Deck aleatorio

Para su implementación se desarrolló un algoritmo en R, de imputación simple, el cual tuvo sus inicios en uno desarrollado con MS Visual FoxPro 9.0 usado para hacer comparaciones de ingresos laborales entre la ENOE y el Módulo de Condiciones Socioeconómicas (MCS) 2015 como parte de los trabajos de investigación que derivaron en el Modelo Estadístico 2015 para la continuidad del MCS-Encuesta Nacional de Ingresos y Gastos de los Hogares.⁴

Al inicio, este algoritmo adiciona un número aleatorio entre 0 y 1 (de una distribución uniforme) a cada observación del conjunto de datos; después, crea dos subconjuntos, uno de donadores con datos completos y otro de receptores con las observaciones con datos faltantes.

A los receptores que declararon menos de 1 salario mínimo se les imputó el salario mínimo multiplicado por el número aleatorio ya asignado. A los que declararon 1 salario mínimo se les imputó este.

Para cada individuo contenido en el subconjunto de datos de receptores que aún no se le ha imputado ingreso se busca uno o varios donadores posibles en el subconjunto correspondiente. Para la búsqueda, se usan las variables antes enlistadas y deben coincidir los valores del receptor con los valores de los posibles donadores. Si se encuentra más de un donador, entonces es seleccionado aquel que tenga el número aleatorio mayor (que le fue asignado al principio) como donador; entonces, el ingreso de este donador es imputado a quien tiene el dato faltante.

Dado que es casi imposible que todos los receptores encuentren un donador incluyendo todas las variables de empate (más de 95% sí encuentra), fue necesario repetir el proceso seis veces más, pero eliminando ciertas variables cada vez.

MICE

Creada por Stef Van Buuren y Groothuis-Oudshoorn (2011), es un algoritmo que implementa la imputación múltiple a múltiples variables a través del método de ecuaciones encadenadas. También, incluye funciones que permiten analizar los datos imputados y apilar esos resultados de acuerdo con las Reglas de Rubin (1987).

Van Buuren y Groothuis-Oudshoorn (1999) explican que MICE asume que para cada variable con datos incompletos se especifica una distribución condicional para los datos faltantes, por ejemplo, para una variable binaria incompleta podría usarse una regresión logística, una politómica para datos categóricos y una lineal para datos numéricos.

Para entender esta metodología, consideremos a X como un vector de variables (X₁, X₂, …, X_j). Con ecuaciones encadenadas se imputa una primera variable X₁ usando X₂ a X_j como explicativas; después, se imputa la variable X₂ usando la X₁ imputada y las X₃ a X_j también como explicativas; luego, se imputa la X₃ usando X₁ y X₂ imputadas y de X₄ a X_j como explicativas y así sucesivamente. Esto lo hace en k iteraciones hasta lograr un conjunto de datos imputado, repitiendo el proceso para las m imputaciones.

MICE implementa 23 métodos de imputación, de los cuales 11 se pueden observar en el cuadro 2. El método a usar dependerá del tipo de la variable con datos faltantes.

Para lo que aquí se presenta, se usaron dos metodologías no paramétricas: pareamiento por medias predictivas (pmm) y bosques aleatorios (rf). Se recomienda el uso de éstas, por ejemplo, cuando la variable en cuestión no presenta una distribución normal, que es el caso de los ingresos laborales de la ENOE.

Pmm, en realidad, es un método Hot Deck con una forma distinta de seleccionar el donador. Para llevarlo a cabo, MICE primero ajusta una variante de un modelo de mínimos cuadrados ponderados; después, agrega ruido a los coeficientes de la regresión; luego, obtiene una predicción de los ingresos en el conjunto de datos imputado (tanto en los casos con ingreso faltante como en los del observado); enseguida, calcula una matriz de distancias entre el ingreso predicho de los casos con ingreso observado y el predicho de los del faltante; a continuación, elige el donador dentro de los d casos con ingreso observado que tengan la distancia más pequeña; el caso seleccionado dona el ingreso observado. Para mayor detalle sobre pmm, ver Van Buuren (2018), Little (1988) y Allison (2015).

La de bosques aleatorios está basada en la técnica de clasificación y regresión implementada en R como randomForest, la cual hace uso de esta. Esta ajusta un bosque aleatorio para cada variable a imputar y el valor asignado al dato faltante será aquel que resulte de un árbol seleccionado aleatoriamente.

Amelia II

Es una herramienta en R para imputación múltiple que puede ser aplicada a datos transversales, series de tiempo y series de tiempo transversales. El algoritmo de imputación múltiple en Amelia asume que los datos tienen una distribución normal multivariada que emplea el algoritmo Expectation Maximization (EM) basado en bootstrap (EMB), descrito por Honaker y King (2010), para imputar los valores. Además, cuenta con funciones de diagnóstico que permiten validar el modelo de imputación.

missForest

Este método para imputación, al igual que MICE rf, hace uso de la técnica de bosques aleatorios implementada en randomForest. Es de imputación simple y funciona muy bien con tipos de variables mezclados, con relaciones no lineales, interacciones complejas y con alta dimensionalidad (cuando hay más variables que observaciones).

Para cada variable, el algoritmo ajusta un bosque aleatorio sobre los datos observados y después predice los faltantes. El proceso se lleva a cabo de forma iterativa actualizando la matriz imputada y midiendo las diferencias entre el valor previo y el nuevo. El proceso iterativo se detiene cuando la diferencia comienza a crecer o cuando se cumple el número de iteraciones indicadas por el usuario. El dato a imputar a la observación con dato faltante será aquella categoría que más se repita en el bosque aleatorio para el caso de variables cualitativas, o bien, el promedio cuando se trate de variables cuantitativas.

Hmisc

Contiene un conjunto de herramientas para la reducción de datos, la imputación, el cálculo de potencia y tamaño de muestra, la creación avanzada de tablas, variables de recodificación, importación e inspección de datos y gráficos generales.

El algoritmo de imputación múltiple de Hmisc toma en cuenta la incertidumbre de las imputaciones mediante bootstraping para aproximarse a la predicción de los valores a partir de la distribución predictiva bayesiana completa. Está basado en modelos semiparamétricos que utilizan los métodos regresión aditiva, bootstraping y pareamiento por medias predictivas.

El algoritmo funciona de la siguiente forma:

1. Para cada variable con NA, inicializa esta con valores de una muestra aleatoria de los valores observados.
2. Realiza lo siguiente “burnin”+”n.impute” veces:
   1. Extrae una muestra con reemplazo del conjunto de datos completo y ajusta un modelo aditivo flexible para predecir los valores de todos los casos.
   2. Imputa cada valor faltante con el observado de la observación, cuyo valor predicho es más cercano al predicho del valor faltante (pareamiento por medias predictivas).

Mi

Es un conjunto de herramientas que permite manipular datos, imputar valores faltantes y analizar conjuntos de datos múltiples imputados, entre otras funciones.

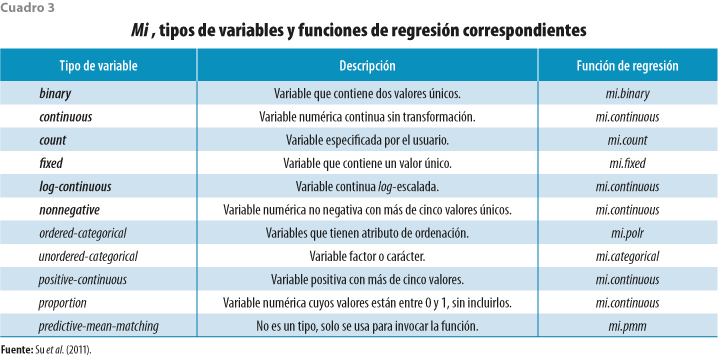
Para que Mi pueda llevar a cabo la imputación múltiple, requiere de una matriz de información construida al configurar el conjunto de datos para la imputación, donde se guarda el tipo de la variable y se propone una función de regresión por aplicar en la imputación, las cuales se muestran en el cuadro 3. Esta matriz puede ser modificada de acuerdo con las necesidades del usuario.

Las funciones mi.continuous(), mi.binary(), mi.count() y mi.polr() ajustan modelos lineales generalizados bayesianos adicionando una distribución t de Student a priori a los coeficientes de regresión. De esta forma mi.polr() usa la función bayespolr() de la librería arm, mientras que mi.continuous(), mi.binary() y mi.count() utilizan bayesglm() de la misma librería, con family=gaussian, family=binomial y family=quasipoisson, respectivamente, para predecir los valores a imputar. La función mi.fixed() solo copia el valor de los observados y mi.categorical emplea multinom(), de la librería nnet, para imputar variables categóricas escalares.

El método de pareamiento de medias predictivas (mi.pmm()), que es el que se eligió en este algoritmo para desarrollar el presente ejercicio, usa bayesgml() para predecir los valores del conjunto de datos completo e imputa cada valor faltante con el observado de la observación cuyo valor predicho es más cercano al predicho del valor faltante.

Rf2e

Este algoritmo de imputación múltiple fue creado específicamente para esta investigación y emplea la técnica de bosques aleatorios de randomForest en dos etapas. En la primera se usa el algoritmo missForest para una primera imputación de todas las variables involucradas, esto con el fin de tomar ventaja del trabajo de imputación de las variables categóricas (desechando la imputación del ingreso).

En la segunda etapa se utiliza como insumo un conjunto de datos creado a partir de las variables categóricas imputadas, en la primera etapa, y la variable de ingreso con datos faltantes. Después, para cada i-ésima (con i = 1, 2, 3, …, m) imputación se lleva a cabo lo siguiente:

1. Se crean dos subconjuntos: unos con datos completos y otro con faltantes.
2. Se extrae una submuestra aleatoria con reemplazo con tamaño igual a 20% del total de observaciones con datos completos (dado que en la mayoría de los trimestres hay más de 100 mil observaciones, la submuestra resultante incluye más de 20 mil).
3. Se entrena el algoritmo randomForest con la submuestra que fue extraída en el paso anterior teniendo a los ingresos como variable a predecir y las otras como predictoras.
4. Usando los resultados del entrenamiento que se hizo en el paso anterior, se predicen los ingresos del subconjunto de datos con ingresos faltantes.
5. El ingreso predicho para cada observación con el faltante es imputado al conjunto de datos resultante de la primera etapa (en su respectiva observación).

4. Resultados

En este ejercicio se contrastaron siete algoritmos diferentes con seis metodologías de imputación, de las cuales dos son para imputación simple (Hot Deck aleatorio y missForest) y cuatro para la múltiple (pmm en MICE, Hmisc y Mi, MICE rf, Amelia II y Rf2e).

Los resultados que aquí se presentan fueron analizados en dos vertientes: en la primera se revisan algunas medidas de desempeño de las metodologías, las cuales pueden funcionar como criterio para elegir la que mejor se adapte a las características de la ENOE; en la segunda se muestran los efectos que puede tener la imputación de ingresos laborales en la ENOE en el ITLP del CONEVAL.

Medidas de desempeño

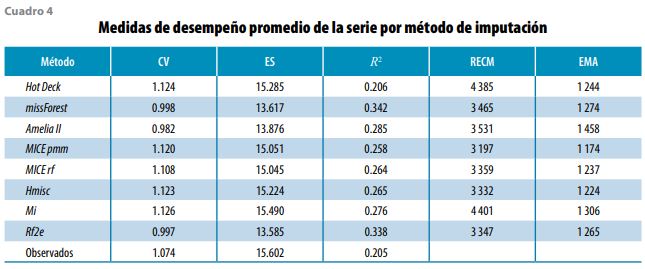
Para valorar el desempeño de cada metodología, se usaron tres medidas que involucran solo a los conjuntos de datos completos: el coeficiente de variación (CV), el error estándar (ES) y el coeficiente de determinación (R²), así como dos que involucran tanto a los conjuntos de datos con valores faltantes como los completos: la raíz del error cuadrático medio (RECM) y el error medio absoluto (EMA), de las cuales puede observarse un resumen en el cuadro 4 expresado en promedios de toda la serie de la ENOE aquí estudiada. Cabe hacer mención que para obtener estas medidas se aplicaron las Reglas de Rubin (1987) para el caso de metodologías de imputación múltiple.

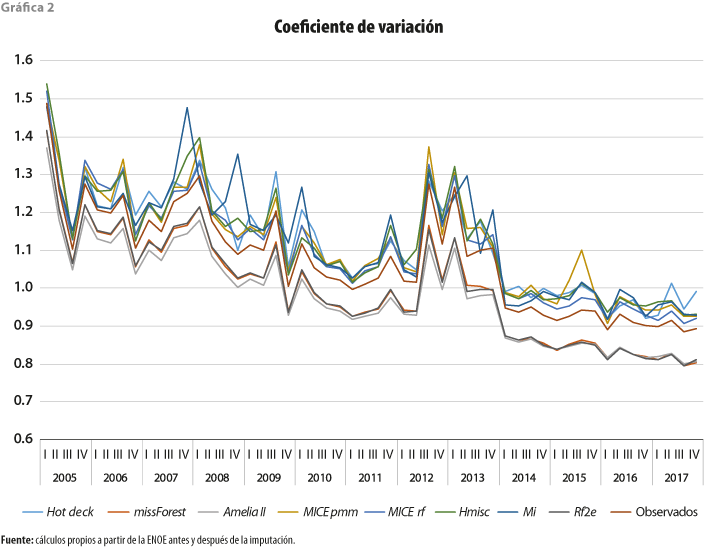
Si se comienza revisando el coeficiente de variación que se observa en la gráfica 2, lo primero que podemos notar es que los ingresos por trabajo de la ENOE (en los datos observados) han tenido una alta variabilidad con una clara tendencia a la baja a través del tiempo; esto contrasta con el incremento que ha reportado la no respuesta de ingresos (faltantes) observada en la gráfica 1b, pudiéndose decir que, conforme incrementa la no respuesta, la variabilidad de los ingresos se compacta (tan es así que la correlación entre ambos es de -0.81).

En la gráfica 2 también podemos notar que los métodos que presentan menor variabilidad entre los ingresos completos son Amelia, Rf2e y missForest (con un CV de 0.98 1.00 y 1.00, respectivamente), incluso presentando menor variabilidad que los datos observados (con CV de 1.07). Con mayor variabilidad que estos últimos, y muy cercanos entre ellos, están MICE rf, MICE pmm, Hmisc, Hot Deck y Mi (con un CV promedio de 1.11, 1.12, 1.12, 1.12 y 1.13, en ese orden).

Dado lo anterior y si el criterio de selección del método fuera aquel que arroje la variabilidad más cercana a los datos observados, el elegido sería MICE rf, aunque los otros con mayor variabilidad también son una buena opción.

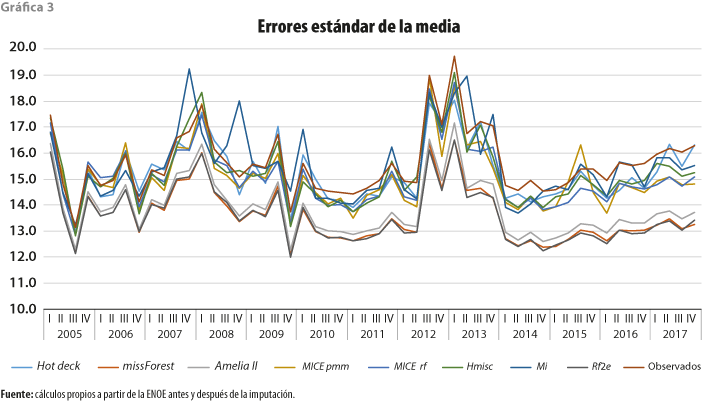
Ahora bien, si lo que se quiere es medir la precisión de la media muestral, entonces es necesario revisar los errores estándar, los cuales se presentan en la gráfica 3. Lo primero que podemos notar es que los ES de los ingresos por trabajo de la ENOE (en los datos observados) han tenido una tendencia estable a la baja a través del tiempo, aunque con una leve tendencia al alza en los últimos años.

También, al observar dicha gráfica, se puede notar que quien arroja mejor precisión es Rf2e (con un ES promedio de 13.59) seguido de missForest (13.62), Amelia (13.88) y, con menos precisión, MICE rf (15.05), Hmisc (15.22), Hot Deck (15.29) e, incluso con la precisión menor, Mi (15.49); por lo tanto, si el criterio de selección es el método que proporcione la mayor precisión de la media, se elegiría Rf2e.

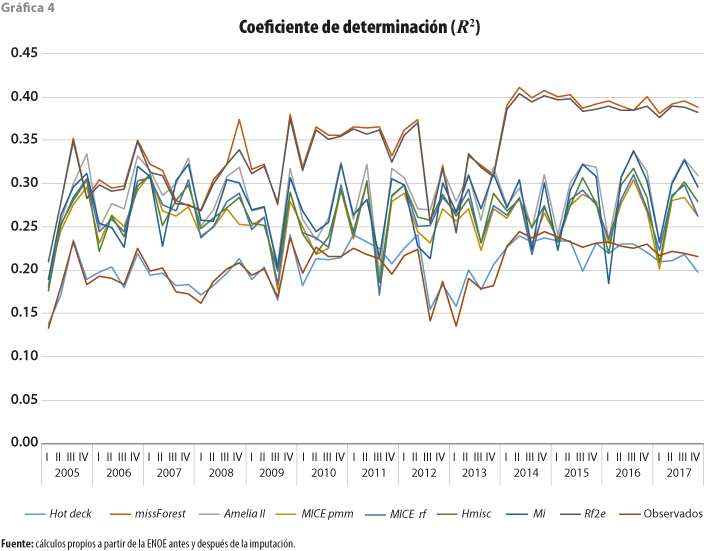
Por otro lado, sabiendo que el coeficiente de determinación se define como la proporción de variación de la variable Y (ingreso) que es explicada por las variables X (las enlistadas anteriormente) en un modelo de regresión, este puede ser usado como una medida de desempeño de la imputación.

Como se puede observar en la gráfica 4, los R² son relativamente bajos, sugiriendo que las estimaciones del modelo no ajustan tan bien a la variable real; esto se debe a la gran variabilidad que se observa en los ingresos laborales mostrada en la gráfica 2, tan es así que, conforme la variabilidad disminuye a través del tiempo, los R² van incrementando; incluso, la correlación entre ambos es de -0.88.

La gráfica 4 también muestra que las metodologías que mejor ajustan son Rf2e y missForest con un promedio en toda la serie de 0.34 (presentando un comportamiento muy similar a lo largo del tiempo), con un repunte entre el 2014 y 2017 (0.39 de promedio); además, son las que siguen el patrón de los datos observados. Después, es seguido por un grupo compacto formado por Amelia, Mi, Hmisc, MICE rf y MICE pmm con promedios de R² de 0.29, 0.28, 0.26, 0.26 y 0.26, respectivamente. Algo separado queda Hot Deck con 0.21 que, incluso, es el más cercano al promedio de R² de los conjuntos de datos observados.

Sabiendo que esta medida no da muy buenos resultados y si, aun así, se usara como criterio de selección, Rf2e o missForest serían dos buenas opciones a elegir.

RECM y EMA son dos medidas que se basan en la distancia entre el valor observado y el imputado de una misma observación, por lo que para poder calcularlos debió ser necesario considerar como 0 los valores faltantes.

Al examinar la gráfica 5, que presenta los RECM, podemos observar un primer grupo muy compacto de métodos con los peores RECM que son Mi y Hot Deck con promedios en la serie de 4 401 y 4 385, respectivamente. En un segundo grupo, también muy compacto, se encuentran Amelia, missForest, Rf2e, MICE rf, Hmisc y MICE pmm con los RECM más bajos en promedio (3 531, 3 465, 3 347, 3 359, 3 332 y 3 197, en ese orden).

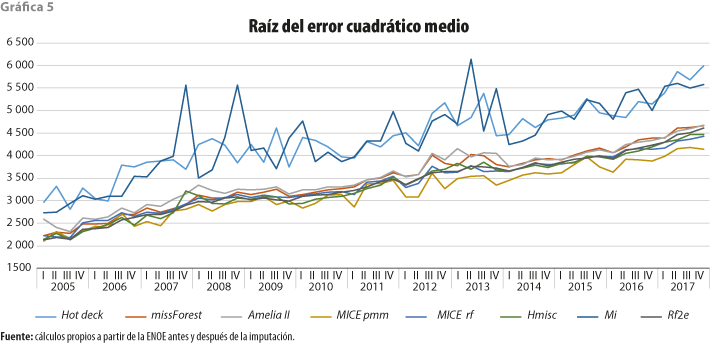
Si se decide seleccionar el método con el menor RECM, se elegiría MICE pmm, aunque cualquiera de los otros cercanos a este representaría una buena decisión.

Por otro lado, al observar los EMA en la gráfica 6, podemos notar que estos presentan, al igual que el RECM, una tendencia creciente en el tiempo (normal si pensamos en los incrementos en el ingreso de los individuos) y que la mayoría de los métodos arrojan EMA muy cercanos los dos primeros años, comenzando a dispersarse a partir del tercero.

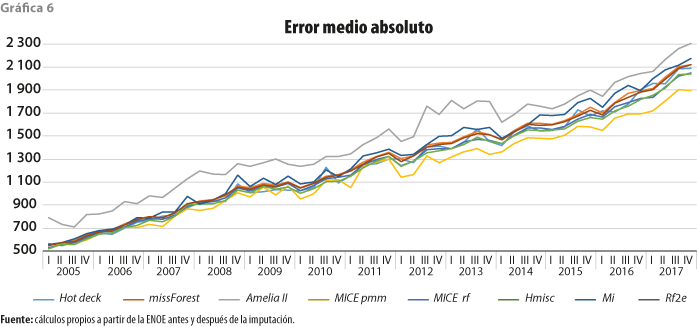
También, podemos percibir que el método con los EMA más bajos es MICE pmm (con un promedio en el tiempo de 1 174); después, separándose un poco, están Hmisc, MICE rf, Hot Deck, Rf2e y missForest (con 1 214, 1 237, 1 244, 1 265 y 1 274, respectivamente); un poco más arriba y con los peores EMA quedan Mi y Amelia (con 1 306 y 1 458, en ese orden).

Al igual que RECM, MICE pmm puede ser la mejor elección si el criterio de selección del método a usar de forma definitiva es aquel que tenga el EMA menor.

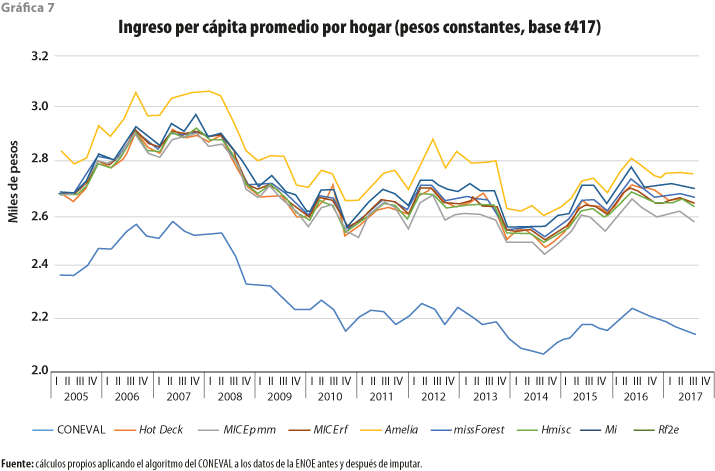
Dado que los expertos se inclinan más por metodologías de imputación múltiple (descartando las de la simple) y observando el cuadro 5, se puede decir que la metodología que mejores resultados presenta es MICE pmm, por su mayor frecuencia. Aunque cualquiera de las que ahí aparecen, excepto missForest, puede ser elegida debido a que los resultados de las métricas son muy cercanos entre ellos.

Efectos de la imputación en el ITLP

Anteriormente se mencionó que el CONEVAL trata como ceros a los ingresos faltantes en la ENOE a la hora de hacer el cálculo del ITLP; incluso, trata como ceros a los ingresos que son reportados como rango de múltiplos de salarios mínimos. También, se dijo que hacerlo de esa forma agrega un fuerte sesgo a cualquier estimación que se lleve a cabo a partir de esos ingresos, estimaciones que, al ser sesgadas, no reflejan la verdadera realidad que se quiere medir.

De acuerdo con lo anterior, para poner en evidencia los efectos que pudiera registrar la imputación de ingresos en la ENOE, se analizaron el ITLP y dos indicadores derivados de este: el ingreso per cápita promedio del hogar y el porcentaje de población con ingreso laboral inferior al costo de la canasta alimentaria.

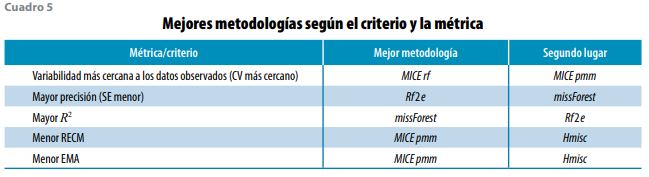
Al revisar primero el ingreso per cápita por hogar, que se aprecia en la gráfica 7, se puede observar que los promedios han tenido una tendencia a la baja a partir del 2007; esto puede deberse, en gran medida, a que los ocupados están subdeclarando sus ingresos. También, se nota que Amelia es la metodología que reporta los incrementos más altos, respecto a los reportados por el CONEVAL en este indicador, con un aumento promedio en el tiempo de 23.5%; después, un poco por debajo, le sigue Mi con 19.9% en promedio; asimismo, formando un grupo compacto, siguen missForest, Rf2e, MICE rf, Hot Deck, Hmisc y MICE pmm con incrementos promedio de 18.7, 18.5, 18.2, 17.9, 17.8 y 16.7%, respectivamente. Dado esto, se puede decir que los ingresos per cápita obtenidos por el CONEVAL están subestimados entre 16.7 y 23.5% en promedio, dependiendo de la metodología que se aborde.

El incremento en el ingreso per cápita debido a la imputación trae como consecuencia una disminución en el porcentaje de población con ingreso laboral inferior a la canasta alimentaria, como se percibe en la gráfica 8, donde se puede notar que Amelia es la que reporta la disminución más alta con 9.4% en promedio con respecto a lo publicado por el CONEVAL; después, formando un grupo compacto, están missForest, Rf2e, MICE rf, Hmisc, MICE pmm y Mi con disminuciones que van de 7.5 a 6.5% en promedio; Hot Deck aparece con la menor disminución (5.6% en promedio) considerando el indicador del CONEVAL.

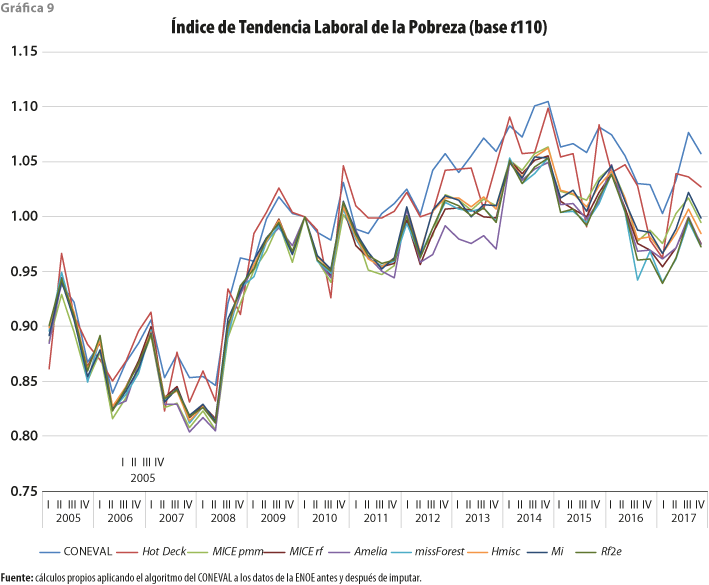
En la gráfica 9 podemos apreciar que la imputación de ingresos en la ENOE provoca una disminución en el ITLP. Incluso, observamos que el método que menos disminuye, con respecto a lo publicado por el CONEVAL, es Hot Deck (alrededor de 1% en promedio), aunque muestra una gran variabilidad en el tiempo. El resto disminuye entre 3 y 4% en promedio, siendo Amelia la que aparece con la mayor disminución.

La imputación de ingresos laborales en la ENOE, entonces, puede contribuir a explicar de mejor manera lo que se quiere medir a través del ITLP.

5. Conclusiones

A lo largo del tiempo, la ENOE ha presentado un incremento permanente en la no respuesta de los ingresos laborales, incluyendo los casos que se reportan en rangos de múltiplos de salarios mínimos, al iniciar en el primer trimestre del 2005 con 10.6% y alcanzando 27.5% en el cuarto del 2017.

La no declaración de ingresos y la declaración en intervalos de múltiplos de salarios mínimos en su conjunto en la ENOE han crecido 0.3% en promedio por trimestre, haciendo que estos dos fenómenos en el futuro sean insostenibles, y aunque la imputación de ingresos faltantes es una opción aceptable para solucionarlo, de seguir al alza estos dos fenómenos, serán más las observaciones con datos imputados que con observados. Ante esto, es necesario que el INEGI tome las medidas necesarias en el diseño de instrumentos de captación y en el operativo de campo para revertir esa tendencia.

Dado que el INEGI publica los microdatos de la Encuesta con esos ingresos faltantes, se planteó hacer un ejercicio de comparación de metodologías de imputación tanto simples como múltiples para poner a consideración de los usuarios de la ENOE la adopción de este procedimiento como parte de la preparación del conjunto de datos para la generación de indicadores, aunque lo deseable es que sea el Instituto quien lo adopte como parte del procesamiento de las encuestas en hogares y ponga a disposición de los usuarios tanto los datos observados como los imputados y toda la información relacionada con el procedimiento de imputación.

Para medir el desempeño de cada metodología, se reportaron un conjunto de métricas (coeficiente de variación, error estándar, R², raíz del error cuadrático medio y el error medio absoluto) que permiten dar una idea de cuál pueda ser la más adecuada por adoptar. En este sentido, ya que los expertos en el tema se inclinan más por las de imputación múltiple, elegir cualquiera de entre MICE pmm, Rf2e, Hmisc y MICE fr puede ser una muy buena opción debido a que los resultados de las métricas son muy cercanos entre ellos, aunque MICE pmm es la que arroja los mejores.

Para cada metodología, también se analizó el efecto que provoca la imputación de ingresos en la ENOE al ITLP y otros indicadores que calcula y difunde el CONEVAL, encontrando lo siguiente:

1. Que los ingresos per cápita obtenidos por el CONEVAL están subestimados entre 16.7 y 23.5% en promedio, dependiendo de la metodología que se revise.
2. Que el incremento en el ingreso per cápita debido a la imputación trae como consecuencia una disminución en el porcentaje de población con ingreso laboral inferior a la canasta alimentaria. Este decremento representa entre 5.6 y 9.4% en promedio, dependiendo de la metodología utilizada.
3. Que el aumento en el ingreso per cápita también provoca una disminución entre 1 y 4% en promedio del ITLP.

Algo que es necesario recalcar es que el ingreso per cápita por hogar ha tenido una tendencia a la baja a partir del 2007 y que esto puede deberse, en gran medida, a una creciente subdeclaración de ingresos por parte de los ocupados. Además, el proceso de imputación, por sí mismo, no corrige esa subdeclaración, ya que se imputan valores restringidos a los que se observaron en cada trimestre.

La imputación de ingresos laborales en la ENOE, por lo tanto, tiende a disminuir el sesgo y permite explicar de mejor manera lo que se quiere medir con el ITLP.

 

___________________

Fuentes

Allison, P. Imputation by Predictive Mean Matching: Promise & Peril. 2015, marzo 5 (DE), recuperado en junio 12 del 2018 de http://bit.ly/2sj6L7Q

_______ Why You Probably Need More Imputations Than You Think. 2012, noviembre 9 (DE), recuperado en junio 12 del 2018 de http://bit.ly/2L4s5od

Campos-Vazquez, Raymundo. Efectos de los ingresos no reportados en el nivel y tendencia de la pobreza laboral en México. Serie documentos de trabajo del Centro de Estudios Económicos, El Colegio de México, Centro de Estudios Económicos, 2013 (DE), recuperado el 11 de junio de 2018 de http://bit.ly/37JAxTy

Durán Romo, B. “Ajuste demográfico por imputación”, en: Realidad, Datos y Espacio Revista Internacional de Estadística y Geografía. Número especial. México, INEGI, 2018, pp. 28-57 (DE), recuperado el 14 de septiembre de 2018 de http://bit.ly/2rAEGbI

Eurostat. “Imputation-Little and Su Method”, en: Memobust Handbook on Methodology of Modern Business Statistics. Eurostat, 2014 (DE), recuperado de http://bit.ly/2pY85fC

James Honaker, J. & G. King. “What to do About Missing Values in Time Series Cross-Section Data”, en: American Journal of Political Science. 54, 3, 2010, pp. 561-581 (DE), recuperado de http://bit.ly/2qTJdpU

Little, R. J. A. “Missing-Data Adjustments in Large Surveys”, en: Journal of Business & Economic Statistics. 6(3), 1988, pp. 287-296 (DE), recuperado de http://bit.ly/2XSJ4z6

Paulin, G., J. Fisher, & S. Reyes-Morales. User’s Guide to Income Imputation in the CE [Ebook]. Washington D.C.: US Department Of Labor. Bureau of Labor Statistics, 2006 (DE), recuperado de http://bit.ly/2OWbxzZ

Peugh, J. & C. Enders. “Missing Data in Educational Research: A Review of Reporting Practices and Suggestions for Improvement”, en: Review of Educational Research. 74(4), 2004, pp. 525-556 (DE), recuperado de http://bit.ly/2R0ZyE2

Reiter, J. & T. Raghunathan. “The Multiple Adaptations of Multiple Imputation”, en: Journal of the American Statistical Association. 102(480), 2007, pp.1462-1471 (DE), recuperado de http://bit.ly/34w08xc

Rodríguez-Oreggia, Eduardo & Bruno López-Videla. “Imputación de ingresos laborales. Una aplicación con encuestas de empleo en México”, en: El Trimestre Económico. 82(325), 2015, pp. 117-146 (DE), recuperado el 8 de junio de 2018 de http://bit.ly/34vgmqz

Rubin, Donald B. Multiple imputation for nonresponse in surveys. New York, Wiley, 1987.

Rubin, Donald B., & Nathaniel Schenker. “Multiple Imputation for Interval Estimation from Simple Random Samples with Ignorable Nonresponse”, en: Journal of the American Statistical Association. 81:394, 1986, pp. 366-374, DOI:10.1080/01621459.1986.10478280.

Starick, R. Imputation in Longitudinal Surveys: The Case of HILDA. Research Paper of the Australian Bureau of Statistics. 2005 (DE), recuperado de http://bit.ly/37O8qT5

Su, Y., A. Gelman, J. Hill, & M. Yajima. “Multiple Imputation with Diagnostics (mi) in R: Opening Windows into the Black Box”, en: Journal of Statistical Software. 45(2), 2011, pp. 1-31 (DE), recuperado de doi: https://bit.ly/2DB3UJN

University of Essex. Institute for Social and Economic Research. British Household Panel Survey: Waves 1-18, 1991-2009. [data collection]. 8th Edition. UK Data Service, 2018, SN: 5151 (DE), recuperado de http://bit.ly/2Dsmq76

Van Buuren, S. Mice. 2018 (DE), recuperado el 19 de junio de 2018 de http://bit.ly/33qFY6n

Van Buuren S. & Groothuis-Oudshoorn K. “Mice: Multivariate Imputation by Chained Equations in R.”, en: Journal of Statistical Software. 45(3), 2011, pp. 1-67 (DE), recuperado de http://bit.ly/2qVdxAj

_______ Flexible multivariate imputation by MICE (Tech. rep. TNO/VGZ/PG 99.054). Leiden: TNO Preventie en Gezondheid, 1999 (DE), recuperado de http://bit.ly/2Orly9h

________________________________________________

¹ Peugh y Enders (2004) describen los mecanismos de datos faltantes como:

• Missing Completely at Random (MCAR) cuando los valores perdidos de la variable X no están relacionados con los valores de las demás variables ni tampoco con los valores subyacentes de la misma variable X.
• Missing at Random (MAR) cuando los valores perdidos de la variable X sí están relacionados con los valores de las demás variables, pero no con los valores subyacentes de la misma variable
• Missing not at Random (MNAR) cuando los valores perdidos de la variable X sí están relacionados con los valores subyacentes de la misma variable X.

² Reglas de Rubín (1987), ver también Rubín y Schenker (1986).

Sea el estimador puntual del i-ésimo conjunto de datos imputado con i=1,2,…,m. Entonces, el estimador para Q sobre las múltiples imputaciones estará dado por el promedio de los m conjuntos de datos completos:

La varianza estimada del estimador puntual estará dada por la combinación de las varianzas intra-imputación y entre-imputación de la siguiente forma: , donde representa las varianzas intra-imputación y la entre-imputación.

El intervalo de confianza estará dado por , con grados de libertad

³ Ya Rodríguez y López (2015) demostraron que la probabilidad de los ingresos faltantes de la ENOE no se da de forma completamente aleatoria (MCAR, ver p. 9 de la versión en PDF).

⁴ Material publicado en el sitio del INEGI en la sección de Investigación: http://bit.ly/2OvI2G9