Indicadores de actividad económica municipal 1993-2013

 

Municipality-Level Economic Activity Indicators 1993-2013

 

Jesús López Pérez y Francisco Corona*
INEGI, jesus.lopez@inegi.org.mx y franciscoj.corona@inegi.org.mx, respectivamente.

Nota: los autores agradecen los comentarios y sugerencias tanto del personal de la Dirección General Adjunta de Cuentas Nacionales del Instituto Nacional de Estadística y Geografía (INEGI) —en particular a Francisco Guillén, Lourdes Mosqueda, Leonel García y Jaime Rodríguez— como de Benito Arciniega, director de la Coordinación de Diseño Conceptual y Estudios Económicos, y en especial a Natalia Volkow por el acceso al Laboratorio de Microdatos del Instituto; asimismo, extienden un reconocimiento por las aportaciones de los participantes en los coloquios de investigación del INEGI, de los dictaminadores anónimos y de Gerardo Leyva Parra, director general adjunto de Investigación; sin lugar a dudas, todos contribuyeron a mejorar este documento.

Vol. 11, Núm. 3  – Epub                                                                         Indicadores de…– Epub

Este trabajo representa una extensión de nuestra investigación del 2019, en la cual construimos estos indicadores (IAEM) basados en los Censos Económicos para el periodo 2003-2013; ahora, extendimos la longitud de las series de tiempo hasta 1993 e incluimos mejoras metodológicas en términos de representatividad económica y geográfica; también, a manera de verificar el funcionamiento en muestras finitas del uso de interpoladores para los años no censales, se estimó un experimento Monte Carlo para diferentes procesos generadores de datos evaluando el desempeño de los interpoladores usados en esta investigación y, asimismo, se verificó la preservación del movimiento entre estimaciones preliminares y finales al hacer uso de la Regla de Combinación (RC) de Guerrero y Peña (2003). Concluimos que los IAEM hasta 1993 cuentan con las características económicas y geográficas representativas que permiten a los usuarios tener una mayor cantidad de información para la toma de decisiones a nivel municipal; asimismo, hay certeza estadística de que el uso de interpoladores lineales minimiza la incertidumbre para la estimación de los años no censales e, igual, se puede comprobar de manera empírica la preservación del movimiento, lo cual garantiza la consistencia de las estimaciones al hacer uso de la RC. Palabras clave: interpoladores; Monte Carlo; Producto Interno Bruto; Regla de Combinación; Valor Agregado Censal Bruto.

This work represents an extension of our 2019 research, in which we constructed these indicators (IAEM) based on the Economic Censuses for the period 2003-2013; now, we extended the length of the time series to 1993 and included methodological improvements in terms of economic and geographic representativeness. In order to verify the functioning in finite samples of the use of interpolators for non-census years, we estimated a Monte Carlo experiment for different data generating processes evaluating the performance of the interpolators used in this research and we also verified the preservation of the movement between preliminary and final estimates by using the Combination Rule (CR) of Guerrero and Peña (2003). We concluded that the IAEMs up to 1993 have the representative economic and geographic characteristics that allow users to have a greater amount of information for decision making at the municipal level. Likewise, there is statistical certainty that the use of linear interpolators minimizes the uncertainty for the estimation of non-census years and the preservation of movement can be empirically verified, which guarantees the consistency of the estimates when using CR.                                                      Key words: interpolators; Monte Carlo; Gross Domestic Product; Combination Rule; Gross Census Added Value.

Recibido: 12 de diciembre de 2019.
Aceptado: 20 de marzo de 2020.

 

Antecedentes

En el 2019 presentamos la primera aproximación formal para la construcción de indicadores^[1] de actividad económica municipal (IAEM) del 2003 al 2013 por Gran Actividad Económica (GA) basados en los Censos Económicos (CE). Para lo anterior, usando información representativa a nivel regional, estimamos para los años censales aproximaciones del Producto Interno Bruto (PIB) de municipios^[2] para los sectores regionalmente representativos; enseguida, hicimos uso de interpoladores lineales para tener estimaciones del PIB para los años no censales; después, utilizando la Regla de Combinación (RC) de Guerrero y Peña (2003), restringimos los resultados preliminares de tal forma que las sumas de dichas estimaciones fueran equivalentes al PIB estatal; finalmente, agregamos la información de los sectores considerados para formar una aproximación por GA.

La metodología fue evaluada de manera empírica para datos estatales, donde se pudo validar un error muestral. Se concluyó que la principal fuente de error era debido a que el uso de los CE no incluía el total de las actividades económicas.

Tal investigación permite a los usuarios tener una metodología que genera información temporal de la actividad económica por municipio, lo cual puede traducirse en realizar una mayor cantidad de análisis de corto plazo y medir, por ejemplo y para el periodo considerado, el funcionamiento de las políticas económicas de los gobiernos locales; sin embargo, debido a que la longitud de las series es relativamente corta, 10 años, se limita el posible uso estadístico y econométrico de los indicadores, situación que con series de tiempo más largas se minimiza, dado que se pueden construir modelos más robustos que permitan entender, de mejor manera, los fenómenos económicos acontecidos.

Para lograr lo anterior, es claro que hay situaciones a considerar, por ejemplo, los diferentes catálogos utilizados por el Sistema de Cuentas Nacionales de México (SCNM) a través del tiempo, es decir, en los CE 1994 y 1999, la categorización de las actividades económicas se realizaba con la Clasificación Internacional Industrial Uniforme (CIIU), mientras que desde el 2003 se utiliza el Sistema de Clasificación Industrial de América del Norte (SCIAN); esto plantea algunas limitantes, ya que es necesario homologar las actividades entre los distintos catálogos. También, es importante señalar que a partir del trabajo de Guerrero y Corona (2018a, 2018b) existe información oficial del PIB estatal año base 2013 hasta 1980, lo cual permite utilizar la RC para generar IAEM, incluso antes del 2003. Asimismo, se considera apropiado evaluar tanto el desempeño estadístico por interpoladores para los años no censales como los supuestos que garantizan la optimalidad de los resultados en un sentido estadístico.

En la actualidad, el artículo 115 constitucional señala que los estados^[3] tienen como base de su división territorial y organización política y administrativa el municipio libre. Desde su concepción, esta instancia ha buscado contar con independencia política y económica; así, parte del discurso de la Constitución de 1917 versa: “… El municipio independiente, que es sin disputa una de las grandes conquistas de la Revolución, como que es la base del gobierno libre, conquista que no sólo dará libertad política a la vida municipal, sino que también le dará independencia económica, supuesto que tendrá fondos y recursos propios para la atención de todas sus necesidades…” (González, 1987).

En consecuencia, es importante que los municipios cuenten con información económica desagregada y con la temporalidad suficiente para la elaboración de sus políticas públicas sustentadas. Además, las entidades federativas requieren de datos a esas escalas para la elaboración de diagnósticos hacia dentro de sus regiones territoriales para poder identificar las disparidades y desigualdades que, por lo común, aparecen en la configuración económica. Es, pues, a través de la observación detallada de la evolución económica de estos territorios que se puede identificar su progreso. Por otro lado, tener claro su tamaño y desempeño diferenciado plantea el hecho de poder diseñar mecanismos que sean capaces de internalizar desde su armado las distintas características de estos en beneficio de los habitantes.

La disponibilidad de estadísticas con este nivel de desagregación permite, también, sensibilizar a los tres niveles de gobierno sobre el rezago de unos municipios con respecto a otros, lo que puede traducirse en el diseño de programas que intenten revertir este comportamiento diferencial. Por ende, la falta de información económica de estos ocasiona limitantes en materia de diseño, análisis y ejecución de políticas públicas.

En México, la disponibilidad de datos a este nivel es, en la mayoría de los casos, para indicadores demográficos, siendo escasos los de carácter económico. Por mencionar algunos ejemplos, el Instituto Nacional para el Federalismo y Desarrollo Municipal, que mantiene el Sistema Nacional de Información Municipal, contiene cierta información política y sociodemográfica y concentra algunos datos de las condiciones laborales de la población a nivel municipal para los años de los censos de población y vivienda del INEGI. Por otra parte, el Sistema Estatal y Municipal de Bases de Datos del INEGI concentra, además de la información anterior, datos de índole municipal con base en registros administrativos y de otras fuentes, por ejemplo: vehículos de motor en circulación, accidentes de tránsito y estadísticas de finanzas públicas; no obstante, esta última presenta un gran número de datos faltantes, además de que la temporalidad de estas dista de ser larga.

La experiencia de otros países muestra que, por ejemplo, la Oficina de Análisis Económico de los Estados Unidos ha publicado en fecha reciente información del PIB a nivel condado; previamente, en Guci et al. (2016), esta institución estableció una agenda de investigación para la medición del PIB a ese nivel de desagregación y cuyos resultados fueron liberados en diciembre del 2019 en la modalidad de prototipo de información.^[4] Otra nación que ya cuenta con datos de este tipo es Ecuador, la cual publica cifras del valor agregado cantonal, pero con la diferencia de que las genera con base en registros contables y no en estimaciones estadísticas.

En México, además de nuestros estudios (2019), existen otros esfuerzos para elaborar indicadores económicos municipales, como los de González-Estrada y Gallegos-Cedillo (2014) y, en fecha más reciente, del Instituto de Información e Investigación Geográfica, Estadística y Catastral del Estado de México (IGECEM, 2019), que los publicó para los 125 municipios de esa entidad utilizando, también, datos de los CE. Sin embargo, la principal limitación de trabajos previos es que en ellos no se hacen consideraciones respecto a la representatividad geográfica de los sectores de actividad económica ni a restricciones de índole sectorial para limitar las cifras preliminares a los datos oficiales, situación que sí se considera en el presente trabajo; asimismo, no realiza ninguna validación estadística de la metodología utilizada.

Introducción

Así, el objetivo de esta investigación es calcular IAEM para todos los municipios para el periodo 1993-2013 usando la RC y haciendo uso de datos de los CE con representatividad geográfica, así como de las recomendaciones emitidas por el SCNM del INEGI para tener información sobre las actividades económicas a este nivel de desagregación de manera fidedigna.

Para cumplir con este propósito, nos basamos en nuestro propio trabajo del 2019 revisando de nuevo el concepto de representatividad económica y geográfica en los CE, homologando catálogos de actividades económicas entre el CIIU y el SCIAN y utilizando como restricciones contemporáneas adicionales las estimaciones provenientes de la retropolación del PIB estatal hasta 1980 realizada por Guerrero y Corona (2018b). También, ya que existen valores atípicos en los CE que pueden limitar el uso de toda la información económica, se recurrió a una corrección de datos basada en la estimación de regresiones usando especificaciones tipo Cobb-Douglas; asimismo, para complementar el análisis, se hizo otro sobre el funcionamiento en muestras finitas del uso de interpoladores para los años no censales estimando un experimento Monte Carlo para diferentes procesos generadores de datos que pueden ocurrir en la práctica cuando se interpolan datos para los años no censales; para finalizar, y muy importante, se verificó de manera empírica la preservación del movimiento entre estimaciones preliminares y finales, lo cual garantiza de forma estadística la consistencia de los resultados al hacer uso de la RC.

Es válido dejar en claro que en este trabajo no se pretende hacer recomendaciones de política económica ni análisis estructurales de los resultados obtenidos sino, más bien, presentar al público en general una opción de estadística oficial validada de manera correcta para tener indicadores económicos municipales con una temporalidad relativamente larga, la cual permita a los usuarios realizar análisis para los fines que se consideren convenientes, algunos de ellos, comentados con anterioridad.

Así, el artículo se divide de las siguientes secciones: en la primera se resume la metodología usada para generar IAEM; en la segunda se presentan los resultados del experimento Monte Carlo; en la tercera se muestran las estimaciones de los indicadores para el periodo 1993-2013 y la validación de la preservación del movimiento; y, finalmente, se dan las conclusiones y consideraciones finales.

Metodología

En esta sección se sintetizan las fuentes de información utilizadas en este trabajo y el procedimiento estadístico para obtener IAEM. Para mayores detalles, se recomienda al lector revisar Corona y López-Pérez (2019), cuyo resumen se presenta en el apartado IAEM con información de los CE.

Fuentes de información

La que representó mayor importancia para esta investigación son los microdatos de los CE 1994, 1999, 2004, 2009 y 2014 del INEGI. No fue posible incorporar los de la edición 1989, ya que esta no dispone de información a ese nivel.

El objetivo de los CE, de acuerdo con la definición del INEGI (2015, 4), es: “… obtener información estadística básica y actualizada, sobre los establecimientos productores de bienes, comercializadores de mercancías y prestadores de servicios, para generar indicadores económicos de México a un gran nivel de detalle geográfico, sectorial y temático…”. En consecuencia, con estos datos estuvimos en condiciones de comprender la estructura y ubicación geográfica de la actividad económica, pudiendo así establecer la composición económica de los municipios que forman el país. Otras fuentes que se usaron son el PIB por entidad federativa del SCNM, la cual se complementó con la información generada al seguir la metodología de Guerrero y Corona (2018), donde obtuvieron un PIB a nivel estatal desde 1993 para 10 grupos de sectores con año base 2013; en otras palabras, homologaron cifras entre el clasificador actual de actividades económicas (SCIAN) y el anterior (CIIU).

Para esta investigación, se utilizó información de los CE que incorpora solo aquellas clases de actividad económica en las que las unidades de observación registren datos referidos al lugar donde estas se realizan (ver cuadro 1), es decir, se excluyeron aquellas en las cuales las unidades censadas presentaron datos que estaban referidos al sitio donde se ubica la oficina matriz o gerencia, pero que en realidad se desarrollan en un área geográfica mayor (INEGI 2015, 12).

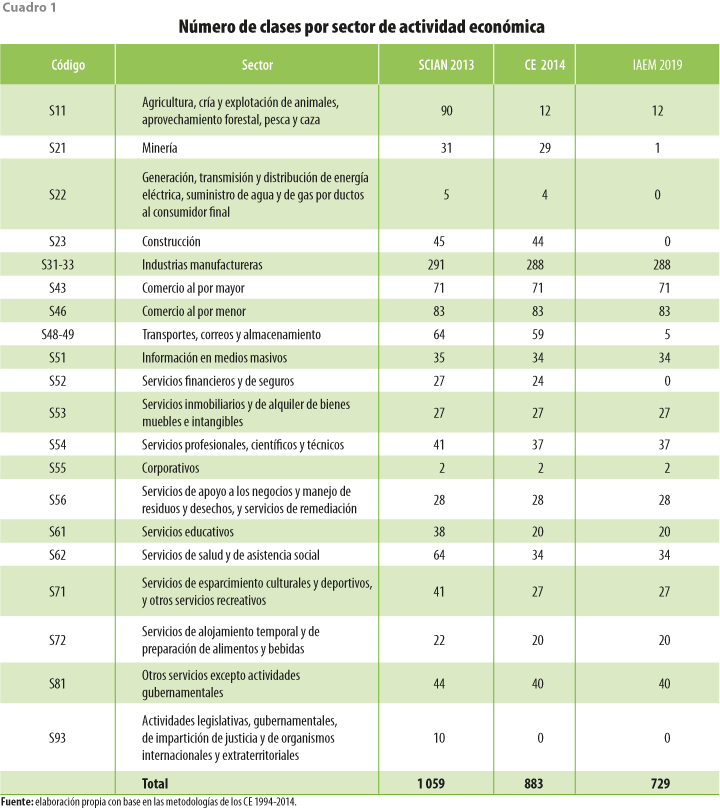
Una vez realizado el análisis de las clases de actividad económica con representatividad regional, se consideró necesario ajustar el sesgo a la izquierda que tiene la distribución del Valor Agregado Censal Bruto (VACB) a través de ajustar la regresión tipo Cobb-Douglas:

log⁡(VACB_i )=a+b₁ log⁡(hrs_i )+b₂ log⁡(Activos_i )+e_i^,

donde el subíndice i = 1, 2, …, n identifica cada establecimiento dentro del sector, hrs_i  son las horas-hombre,  Activos₁ son los activos totales y e_i representa el error aleatorio; finalmente, los parámetros b₁ y b₂ son las elasticidades atribuibles a los factores de la producción y  a es el intercepto.

De esta manera, las cifras atípicas del VACB se ajustan con los coeficientes estimados de a, b₁ y b₂. Es importante señalar que esto se realizó a consideración de la Coordinación de Diseño Conceptual y Estudios Económicos del INEGI.

En las gráficas 1 se muestran los coeficientes de estas estimaciones; en estas es posible observar la consistencia de los parámetros calculados a través del tiempo, salvo para el sector 55, donde la línea azul (que representa el parámetro asociado al número de horas-hombre trabajadas) decrece durante todo el periodo, la cual se puede ver que, de manera consistente, se encuentra por arriba de la línea verde (que es el parámetro asociado a los activos totales).

Se puede apreciar que, con excepción de los corporativos, las elasticidades tienen el mismo comportamiento, es decir, el VACB crece porcentualmente más dado cambios porcentuales en las horas-hombre que cuando lo hacen los activos.

Como resultado de las estimaciones anteriores, se procedió con el ajuste de los datos por el sesgo, lo cual derivó en que la cola izquierda de la distribución fuera más corta y se mostrara asimétrica hacia ese lado. En las gráficas 2 se presenta una comparación de las densidades del VACB por sector de actividad económica: en negro antes de la corrección y en rojo una vez corregido el sesgo hacia la izquierda.

Se puede ver cómo las distribuciones de los datos ajustados no están tan cargadas hacia la izquierda, lo cual es congruente al ajustar el VACB usando la especificación Cobb-Douglas. Vale la pena destacar que los datos considerados como atípicos son a los que se les asignó el valor ajustado o corregido; caso contrario, se considera el VACB observado.

Para visualizar el porcentaje que cubren los CE en el total de la economía y, también, las cifras —considerando solo las clases de actividad económica con representatividad regional— se computaron para cada nueve grupos de sectores^[5] los porcentajes de cobertura promedio, es decir:

 

donde el subíndice representa cada uno de los cinco años censales utilizados en este trabajo y la Cobertura_h se define como   .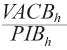

La gráfica 3 muestra los promedios, mínimos y máximos de los porcentajes de cobertura.

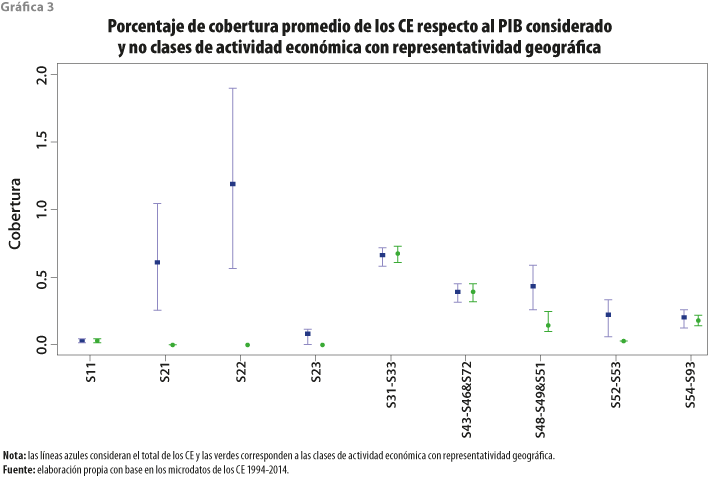
Se aprecia que, para S21, S22 y S52-S53, la cobertura se reduce de manera drástica respecto al total a lo que consideran los CE; no obstante, por lo comentado con anterioridad, en términos de representatividad regional se concluye que estos reflejan mejor la dinámica de las actividades económicas de los sectores en los municipios. Nótese que, en algunos casos, la cobertura de los CE es mayor que la reportada por el SCNM; sin embargo, al corregir solo con clases de actividad económica con representatividad regional, ya no ocurre esta situación, por ejemplo, en S31-S33 y S43-S46&S51. También, las cifras ligeramente mayores, al considerar las clases de actividad económica regional, vienen dadas por el ajuste de la regresión Cobb-Douglas.

Veleros et al. (2011) exponen con más detalle las principales razones que explican las discrepancias para los CE con datos referidos al 2003 y 2008, entre las que destacan: cobertura de sectores económicos (los CE no consideran al agropecuario, transporte y sector público); los diferentes criterios contables de las empresas productoras de cada entidad; que el SCNM realiza estimaciones de la actividad informal (22.7 % en el 2017) y es, en especial, relevante en los sectores de agricultura (80 %), comercio al por menor (54 %) y construcción (44 %); la valoración de los CE a precios de productor, mientras que el SCNM lo hace a básicos; y la representatividad geográfica de las cifras de los CE.

El SCNM (INEGI, 2010, 8) establece: “… por lo expuesto, es posible afirmar que el VACB y el PIB calculado por el SCNM, no son comparables en sentido estricto. Ambas estadísticas pretenden divulgar datos relevantes del acontecer económico y ninguna de las dos tiene preeminencia sobre la otra, sino que deben ser dimensionadas de acuerdo con los propósitos que persiguen…”.

Atendiendo al criterio de representatividad geográfica, el presente trabajo excluye entre 21 y 42% de la información de los CE; la principal diferencia derivada de las exclusiones radica en la cobertura de los sectores 21 (minería) y 22 (energéticos), mientras que en el 11 (actividades primarias) y 23 (construcción), ya de por sí, la cobertura de los CE es muy baja.

La gráfica 4 muestra el porcentaje promedio de cobertura respecto al PIB por entidad federativa, así como su nivel máximo y mínimo considerando todos los CE utilizados en esta investigación.

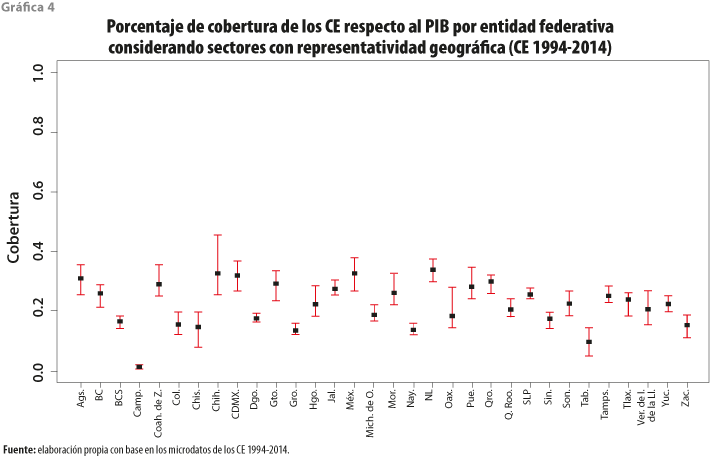
A nivel estatal, las coberturas se encuentran por debajo de 50%, donde el más bajo es para Campeche derivado, sobre todo, de la exclusión de los sectores minero y energético. Ello da cuenta de que el VACB y el PIB calculados por el SCNM no son del todo comparables en sentido estricto; de esta manera, algunos sectores tenderán a representar mejor la dinámica que otros, sobre todo cuando su actividad económica se realice en un espacio físico determinado, como las manufacturas. De esta forma, el VACB y el PIB pretenden divulgar datos relevantes del acontecer económico y ninguno de los dos tiene preeminencia sobre el otro, sino que deben ser dimensionados de acuerdo con los propósitos que persiguen (INEGI, 2010); no obstante, en un sentido econométrico, se pueden obtener estimaciones preliminares que, una vez impuestas las restricciones contables, aproximen de mejor manera lo que se desea calcular, hecho que se considera en este trabajo.

Una vez realizado este análisis se pudo concluir que, establecidas la representatividad geográfica y sectorial —dada esta por la cobertura y agrupación de la información oficial— para la construcción de los IAEM, se deberían considerar los siguientes grupos de sectores (entre paréntesis se muestra la cobertura de los IAEM respecto al SCIAN):

• S31-33: Industrias manufactureras (99 %).
• S43-46 & S72: Comercio y Servicios de alojamiento temporal y de preparación de alimentos y bebidas (99 %).
• S54-S81: Servicios no financieros (70 %).^[6]

IAEM con información de los CE

Para los detalles de notación estadística formal, se recomienda al lector revisar Corona y López-Pérez (2019). La idea general fue, primero, obtener estimaciones preliminares, las cuales, después, debían satisfacer restricciones oficiales, en este caso, que las sumas de los IAEM equivalieran a su respectivo agregado captado del SCNM obteniendo, así, estimaciones finales. En este artículo resumimos el procedimiento para su respectiva aplicación, que consiste en los siguientes pasos:

1. Para cada entidad y año censal, construir razones de VACB por grupo de sectores de actividad económica considerados, de tal forma que la suma de los municipios sea equivalente a 1.
2. Para cada grupo de sectores de actividad económica, estimar los años no censales usando interpoladores que pueden ser, por ejemplo: lineales, cuadráticos o cúbicos. Se considera la fecha de fundación de los municipios. Estos cálculos se consideran como preliminares.
3. Aplicar la RC de Guerrero y Peña (2003), donde la matriz de ponderación se obtiene siguiendo a Corona y López-Pérez (2019) para reconciliar las cifras preliminares, de tal forma que los IAEM del paso anterior sumen a su respectivo dato otorgado por el SCNM. Nótese que esta fase de reconciliación permite expresar los IAEM a año base 2013. Estas se consideran como las estimaciones finales.
4. Se pueden agregar los IAEM para obtener niveles superiores de agregación.
5. Se considera prudente expresar los IAEM como índices de volumen físico dado que el porcentaje de cobertura no es el total.

Nótese que el paso 2 conlleva a un error de estimación. En Corona y López-Pérez (2019) se puede ver que los interpoladores lineales minimizan el error de estimación cuando se supone que queremos estimar el PIB estatal a través de los CE y siguiendo la metodología aquí presentada; no obstante, esto puede resultar limitativo solo a este conjunto de datos, por lo que, en este trabajo, se complementó este análisis a través de un experimento Monte Carlo, donde se simularon las condiciones bajo las cuales se interpolaron cifras.

Experimento Monte Carlo: evaluando el uso de interpoladores para años no censales

Con el objetivo de analizar el rendimiento en muestras finitas del uso de interpoladores para estimar datos faltantes en series de tiempo —explícitamente en este caso para los años no censales—, se estimó un experimento Monte Carlo simulando series con diferentes comportamientos estocásticos, es decir, estacionarias, estacionarias con tendencia determinística y caminatas aleatorias. Se pretendió que emularan características similares a las que tienen las anuales que desean ser estimadas. Lo anterior proporcionará información sobre el costo estadístico de usar como variables preliminares series de tiempo provenientes de una fase de estimación previa.

Se utilizaron siete procesos generadores de datos con una dimensión temporal de T = 21, es decir, el horizonte temporal de los IAEM, los cuales son:

M1. y_t=μ+ϕy_t-1+ε_t donde ϕ~U(0.5,1).
M2. y_t=μ+γε_t-1+ε_t donde γ~U(0.5,1).
M3. y_t=μ+ϕy_t-1+γε_t-1+ε_t donde ϕ y γ ~U(0.5,1).
M4. y_t=μ+0.5y_t-1+0.2t+ε_t.
M5. y_t=μ+0.5ε_t-1+0.2t+ε_t.
M6. y_t=μ+0.5y_t-1+0.5ε_t-1+0.2t+ε_t.
M7. y_t=μ+y_t-1+ε_t.

En todos los casos se supuso que μ=100 y ε_t~N(0,1). Se consideraron conocidos solo t=1, 5, 9,13, 17 y 21 y se aplicaron los interpoladores que utilizamos en la investigación del 2019, los cuales son el uso del interpolador lineal (S_L), en el que se unen los puntos a través de una proporcionalidad lineal entre los datos faltantes (S_SP), donde se ajusta una posición cúbica exacta a través de los cuatro puntos en cada extremo de los datos y el de Stineman (1980) denotado como S_ST, donde se computan pendientes más bajas cerca de pasos o picos abruptos en la secuencia de puntos. Denotamos a w_t, como la estimación de y_t y se estimó el coeficiente de correlación ρ=corr(y_t,w_t) en cada una de las R = 500 réplicas. Se presentaron los cuantiles de ρ(0.05, 0.5, 0.95) para los datos en niveles como la primera diferencia del logaritmo. El cuadro 2 resume los resultados para los niveles de las series.

 

Se puede apreciar que, en todos los casos, el interpolador lineal supera a sus respectivos competidores y solo cuando los modelos cuentan con medias móviles sin tendencia el ajuste es débil; no obstante, cuando las series de tiempo tienen un comportamiento autorregresivo o no estacionario, ya sea determinista o estocásticamente, el S_L es muy competitivo; a este le sigue el S_ST y, por último, el S_SP.

Es importante señalar que, para todos los casos, la caminata aleatoria se ajusta relativamente bien, aunque los resultados deben ser tomados con cautela, pues la correlación solo es válida si las series de tiempo son cointegradas. El cuadro 3 muestra lo mismo que el 2, pero para las primeras diferencias del logaritmo.

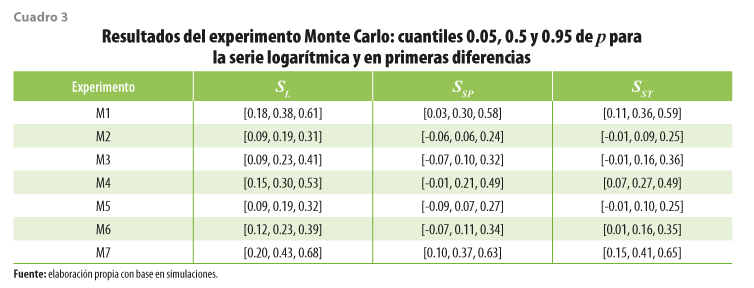
En todas las situaciones, el S_L fue el que obtuvo mejores resultados. En este caso, todas las correlaciones para este interpolador fueron significativas. También, se corrobora que conforme más tendencias tengan las series de tiempo mejor será el ajuste que se obtenga al momento de utilizar los interpoladores, aun cuando las series estén en primeras diferencias.

Se realizaron diferentes experimentos Monte Carlo variando el número de puntos a estimar, mayores y menores a T = 21, y se pudo concluir que los resultados por interpolador son insensibles al tamaño de muestra, es decir, los obtenidos en los cuadros 2 y 3 no se ven modificados de manera estadística.

Por último, con el fin de verificar las condiciones del proceso de simulación, se ajustaron modelos ARIMA a las series del PIB de las 32 entidades federativas para el periodo 1993-2013^[7] por GA y el total de actividad económica (128 series), para lo cual se utilizó la función auto.arima del paquete forecast en el programa R. Los resultados se muestran en la gráfica 5.

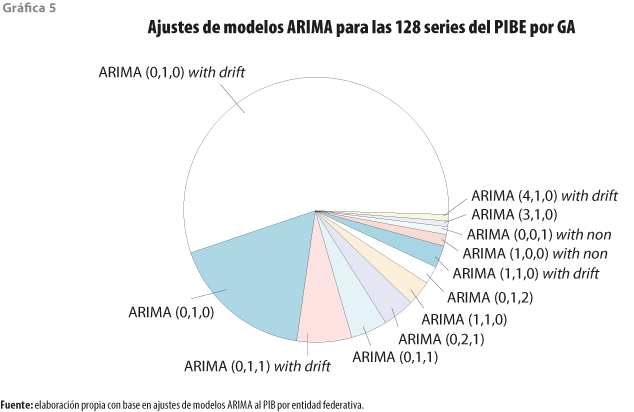
Se puede ver que las condiciones en las que fue generado el experimento abarcan, de buena forma, las características de las series estatales observadas; la mayor parte de estas se ajustan con un modelo ARIMA (0, 1, 0) con deriva, es decir, caminatas aleatorias, las cuales son incluidas en el experimento Monte Carlo de este trabajo.

Nótese que este ejercicio de simulación es independiente de los resultados y/o de la aplicación de la metodología propuesta, solo informa o describe datos sobre el error de estimación que se puede obtener al hacer uso de interpoladores para los años no censales, el cual se minimiza usando el lineal.

Resultados: IAEM

En esta sección se presentan los indicadores calculados para los 20 municipios que al 2013 registraron mayores niveles de actividad económica en el total. En primer lugar, están los resultados para todos los sectores considerados; enseguida, para las industrias manufactureras; y, por último, para los servicios no financieros que corresponden a la suma de los grupos de sectores contenidos en S43-48 y S54-S81. En todos los casos se muestran las estimaciones preliminares y las finales obtenidas al aplicar la RC.

Como se mencionó anteriormente, los IAEM que se obtuvieron no consideran el total de las actividades económicas en el sentido del SCNM, sino que son un reflejo de las que se pueden atribuir al lugar donde se desempeña la actividad económica, en este caso al municipio usando la representatividad geográfica contenida en los CE (ver gráficas 6).

 

Los resultados muestran que la delegación Miguel Hidalgo encabezó la lista con el mayor nivel de actividades económicas, seguida por los municipios Monterrey y Guadalajara. Se puede observar que la Miguel Hidalgo y Monterrey tuvieron un crecimiento desde 1996 hasta el 2008, pero a partir de esta última fecha presentaron una reducción; en cambio, Guadalajara mostró una caída en todo el periodo de análisis. En el 2013, los tres concentraron 10.8% del total, mientras que los 17 restantes más grandes en conjunto acumularon 37.66 por ciento.

Los resultados para las primeras diferencias del logaritmo, es decir para las variaciones porcentuales anuales, se muestran en las gráficas 7.

Las variaciones porcentuales anuales nos indica que, a pesar del uso de interpoladores lineales, la técnica de abajo hacia arriba —la cual consiste en agregar por grupos de sectores y dada la utilización de la RC— permite que las variaciones se muestren persistentes en todo el periodo, llamando la atención las caídas en 1995 y el 2009. De manera general, la Miguel Hidalgo y el municipio San Pedro Garza García son los que exhibieron las tasas de crecimiento más pronunciadas al final del periodo, mientras que la Cuauhtémoc y Monterrey mostraron ligeros decrecimientos en el 2013.

Es de interés observar que hay territorios que exhibieron caídas pronunciadas en sus tendencias (la Miguel Hidalgo, Guadalajara, la Benito Juárez y Álvaro Obregón), mientras que, por otro lado, los que crecieron de manera llamativa (Monterrey, la Cuauhtémoc y Azcapotzalco, Zapopan, Hermosillo y San Luis Potosí). Las gráficas 8 muestran los niveles de los IAEM para las industrias manufactureras y las 9 presentan lo mismo, pero para las primeras diferencias del logaritmo.

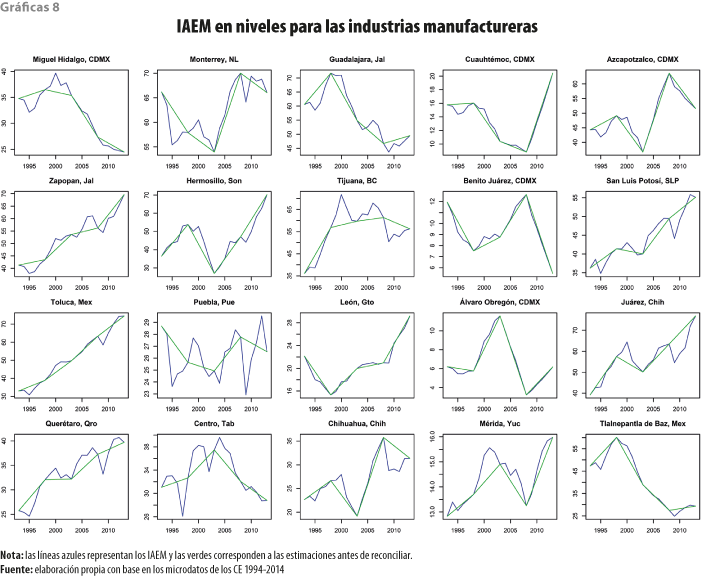
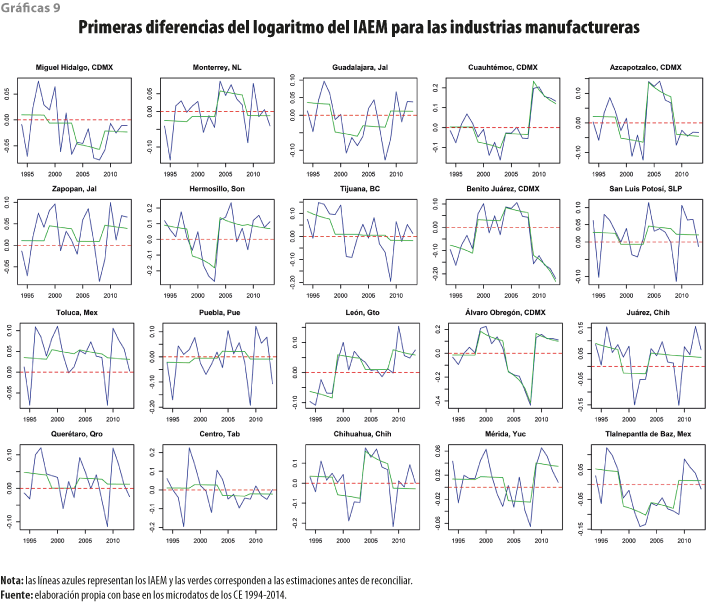
En términos porcentuales, las industrias manufactureras exhibieron variaciones negativas para una gran cantidad de municipios durante el último periodo, donde destacaron la Miguel Hidalgo y Cuauhtémoc, así como Zapopan. Por otra parte, sobresalieron las positivas de la Cuauhtémoc, Monterrey y Guadalajara.

Para los servicios no financieros, las tendencias de los IAEM, en casi todos los casos, presentaron una creciente clara, lo cual fue consistente con el PIB de la GA3 que presentaron todas las entidades federativas; sin embargo, de 1999 al 2003, la Cuauhtémoc mostró una caída, se recuperó en el 2008 y volvió a caer a partir de esa fecha. Los que, aunque con tendencia creciente, tuvieron una ligera caída en los últimos periodos son la Miguel Hidalgo y Monterrey.

Los resultados para los servicios no financieros en niveles se presentan en las gráficas10, y las 11 muestra esto mismo, pero para las variaciones porcentuales anuales.

 

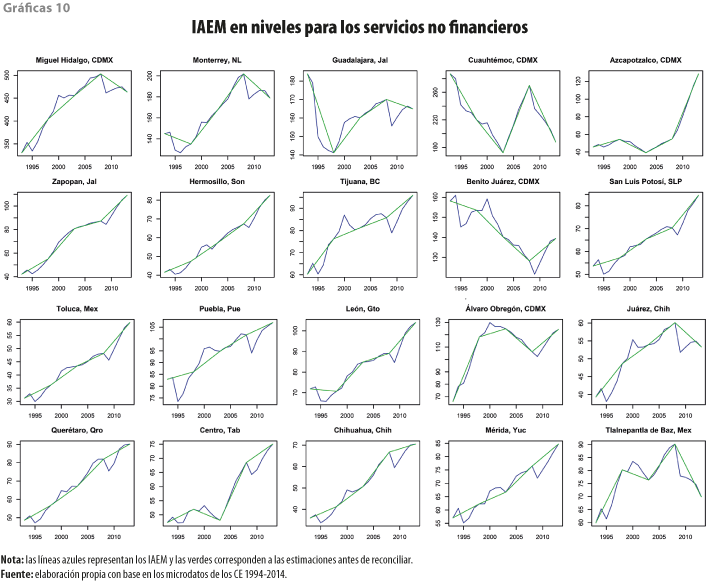
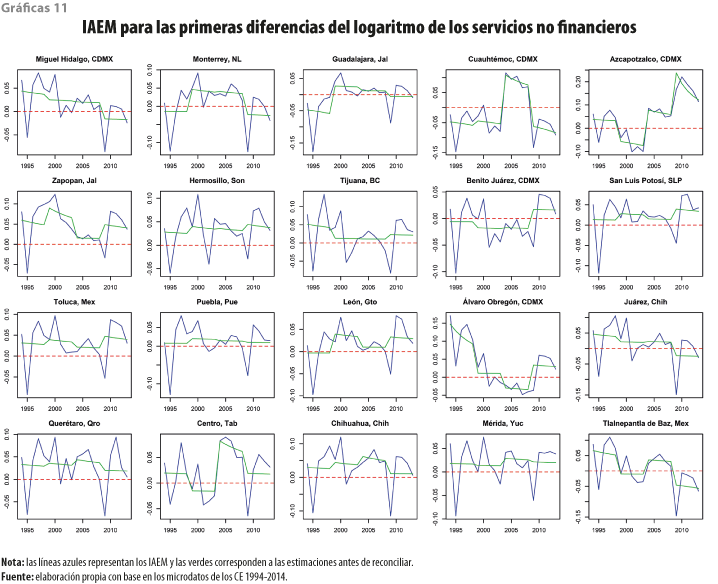
Las variaciones porcentuales anuales de los grupos de sectores que representan a los servicios no financieros mostraron características peculiares; llaman la atención las caídas por las crisis de 1995 y el 2009 para casi todos los municipios; los que, en el último dato, presentaron variaciones negativas son la Miguel Hidalgo, Monterrey, Guadalajara y la Cuauhtémoc.

Para verificar la preservación del movimiento, lo cual garantiza la consistencia de las estimaciones finales de acuerdo con Guerrero y Peña (2003), se calculó para cada municipio la diferencia entre la preliminar y la final, denotada como D_t ; después, nos centramos en verificar que dicha diferencia estuviera centrada en 0, o sea, que no hubiera sesgo y, también, que no se encontrara autocorrelacionada, es decir, que la diferencia fuera ruido blanco. Para constatar el no sesgo, se realizaron pruebas t, cuyos resultados se resumen en el cuadro 4.

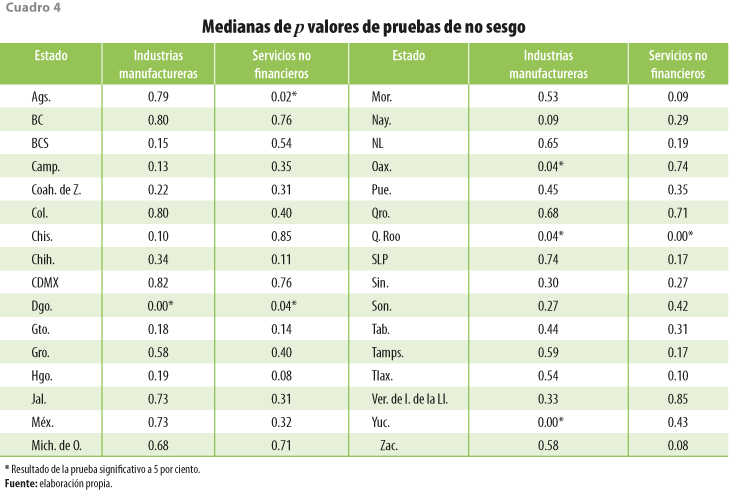
Se puede observar que, con excepción de pocos casos, en la gran mayoría no existe sesgo entre las estimaciones preliminares y finales, es decir, la resta entre ambas series está centrada en 0. En los que no sucede esto, por ejemplo, son para los IAEM de los servicios no financieros de Aguascalientes, Durango y Quintana Roo.

Para verificar que D_t no estuviera autocorrelacionada, se estimaron pruebas Ljung-Box utilizando un rezago de ρ = 4, considerando que es el número de periodos entre cada censo. Los resultados se resumen en el cuadro 5.

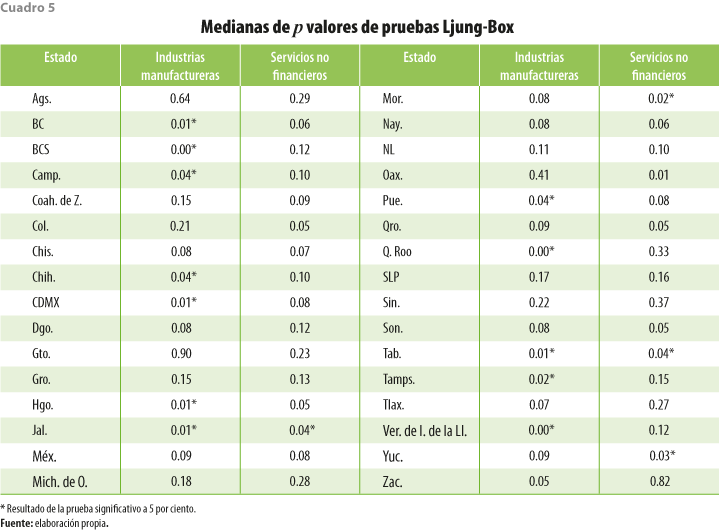
De igual manera, se aprecian algunas excepciones donde no se puede validar que D_t sea ruido blanco. Algunos ejemplos para las industrias manufactureras son Baja California, Baja California Sur, Campeche y Chihuahua, entre otros; no obstante, la gran mayoría de las diferencias están no autocorrelacionadas.

Cabe destacar que aun cuando no se pudo validar la preservación del movimiento y, por ende, la consistencia estadística de las estimaciones para algunos municipios, estos IAEM son la primera aproximación formal del comportamiento económico a ese nivel sectorial, geográfico y temporal de la cual se tiene conocimiento, siendo importante su análisis estructural para los fines que el usuario considere conveniente.

Para terminar, y complementar el análisis, se obtuvieron las tasas medias de crecimiento anual (TMCA) en el periodo 1993-2013 para los 2 457 municipios considerados, y se encontró que 1990 registraron una variación positiva, 449 las tuvieron negativas y 18 se mantuvieron sin cambio (ver mapa).

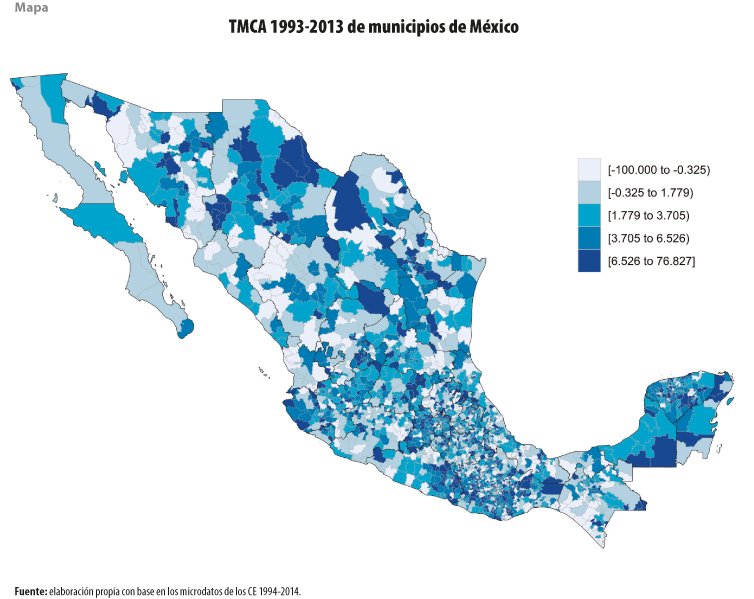
Por tamaño de población, para los 11 municipios con más de 1 millón de habitantes (al 2013), los que tuvieron mayores TMCA son Zapopan, Jalisco (3.89 %), Ciudad Juárez, Chihuahua (2.56 %), y Tijuana, Baja California (2.31 %), mientras que los que registraron las menores, la Gustavo A. Madero, CDMX (- 0.96 %), Guadalajara, Jalisco (-0.65  %), y Nezahualcóyotl, estado de México (0.39 %).

Para los 210 con más de 100 mil habitantes y menos de 1 millón, los que mostraron TMCA más altas en el periodo son El Marqués, Querétaro (19.1 %), Solidaridad, Quintana Roo (15.83 %), y Silao de la Victoria, Guanajuato (13.42 %); los que tuvieron niveles más bajos son Chiapa de Corzo, Chiapas (- 8.66 %), Taxco de Alarcón, Guerrero (-5.6 %), y Chilón, Chiapas (-4.31 %).

Por último, para los 938 con más de 15 mil habitantes y menos de 100 mil, los que presentaron mayores TMCA son Bacalar, Quintana Roo (76.83 %), San Jacinto Amilpas, Oaxaca (28.97 %), y Tepezalá, Aguascalientes (26.88 %); los que tuvieron menores tasas son Noria de los Ángeles, Zacatecas (-16.62 %), Atoyac, Veracruz de Ignacio de la Llave (-12.45 %), y Huixtán, Chiapas (-9.26 %).^[8]

Conclusiones

En este artículo se presenta la metodología basada en Corona y López-Pérez (2019) para generar IAEM hasta1993. Se incluyeron algunas mejoras metodológicas, como tomar solo clases de actividad económica con representatividad municipal; a manera de complementar el análisis, se realizaron experimentos Monte Carlo para tener certeza estadística del uso de interpoladores para los años no censales; y se verificó el principio de preservación del movimiento que garantiza estadísticamente la consistencia de las estimaciones al hacer uso de la RC. Se puede observar que, dado lo anterior, lo que subyace también en utilizar un enfoque de abajo hacia arriba y la incorporación de restricciones contemporáneas, es decir, limitar la suma de los IAEM al total estatal por grupo de sectores, estos permiten capturar la dinámica de las actividades económicas a ese nivel de desagregación.

Se concluye que esta metodología permite a los usuarios de información económica contar con series más largas para analizar la evolución de los municipios y, por ende, generar políticas en este tema; no obstante, se recomienda tener en consideración que los IAEM, al generar un panorama global de las actividades económicas, en ningún caso pueden considerarse medidas del PIB, esto debido a que la información con la cual se construyen no abarca el total de estas de dichos ámbitos territoriales, sobre todo por la naturaleza de los CE y al uso de técnicas estadísticas para generar los IAEM; sin embargo, se considera un trabajo que combina el enfoque de micro y macrodatos para dar solución a un requerimiento de la sociedad.

Como líneas futuras de esta investigación, se recomienda adecuado usar las cifras generadas en este trabajo como estadísticas experimentales en el INEGI, a manera de incentivar su uso y discusión dentro de la sociedad. También, se pretenden actualizar los resultados una vez que se tengan los datos de los CE 2019.

 

______________

Fuentes

Corona, Francisco y Jesús López-Pérez. “Obteniendo indicadores de actividad económica municipal basados en información representativa de los Censos Económicos”, en: Realidad, Datos y Espacio Revista Internacional de Estadística y Geografía. 10(2). 2019, pp. 62-81.

González, Luis. “Conformación política y jurídica del municipio: la incógnita del municipio mexicano”, en: De Lameiras, Brigitte B. (ed.). El municipio en México. El Colegio de Michoacán, 1987, pp. 143-156.

González-Estrada, Adrián, y Gilberto Gallegos-Cedillo. “El producto interno bruto de los municipios de México: II. Estados MZ”, en: Revista Mexicana de Ciencias Agrícolas. 5(8), 2014, pp. 1405-1421.

Guci, Ledia, Charles Ian Mead y Sharon D. Panek. A Research Agenda for Measuring GDP at the County Level. US Department of Commerce, Bureau of Economic Analysis. 2016.

Guerrero, Víctor M. y Daniel Peña. “Combining multiple time series predictors: a useful inferential procedure”, en: Journal of Statistical Planning and Inference. 116(1), 2003, pp. 249-276.

Guerrero, Víctor M. y Francisco Corona. “Retropolación hasta 1980 de algunas series del Sistema de Cuentas Nacionales de México”, en: Realidad, Datos y Espacio Revista Internacional de Estadística. 9(3), 2018, pp. 98-119.

INEGI. Metodología de los Censos Económicos 2014. Aguascalientes, INEGI, 2015.

_______ Sistema de Cuentas Nacionales de México. Producto Interno Bruto por entidad federativa 2003-2007. Aguascalientes, INEGI, 2010.

Instituto de Información e Investigación Geográfica, Estadística y Catastral del Estado de México (ICEGEM). Producto Interno Bruto Municipal. Gobierno del Estado de México, Secretaría de Finanzas, 2019.

Stineman, Russell W. “A Consistently Well Behaved Method of Interpolation”, en: Creative Computing. 6(7), 1980, pp. 54-57.

Veleros, Zeus, Salvador Hernández, Gonzalo Dolores de la Merced y César Amador Ambriz. “Fundamento metodológico, discrepancias estadísticas y errores conceptuales en el uso de datos económicos”, en: Paradigma Económico. 3(1), 2011, pp. 71-110.

___________________

^[1] Nos referimos al término en plural por la naturaleza econométrica con la que se construyen, es decir, se tienen diferentes indicadores según su fase de estimación, restringiendo finalmente y de manera contemporánea con datos oficiales de índole estatal; no obstante, como resultado final, el lector puede considerar como sinónimos los términos indicadores e indicador.

^[2] A lo largo de todo el documento, por simplicidad, cuando nos referimos a los municipios en general abarcamos también a las delegaciones (hoy demarcaciones territoriales) de la Ciudad de México.

^[3] Incluye la Ciudad de México con sus demarcaciones territoriales.

^[4] https://bit.ly/2GVW4iX

^[5] Concentran una serie de actividades económicas que tienen en común el origen de las mismas: 1) Agropecuario, silvicultura y pesca; 2) Minería; 3) Industria manufacturera; 4) Construcción; 5) Electricidad, gas y agua potable; 6) Comercio, restaurantes y hoteles; 7) Transporte, almacenamiento y comunicaciones; 8) Servicios financieros, seguros y bienes inmuebles; y 9) Servicios comunales, sociales y personales.

^[6] No se incluye el S72.

^[7] Series que consideran los cálculos del SCNM y no incluyen al periodo de retropolación.

^[8] Existen, además, 1 298 municipios con menos de 15 mil habitantes.