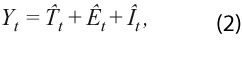Inclusión del calendario mexicano en el proceso de desestacionalización de series de tiempo: el caso del Indicador Global de la Actividad Económica

 

Inclusion of the Mexican Calendar in the Process
of Seasonal Adjustment of Time Series: the Case of the Global Economic Activity Indicator

Francisco de Jesús Corona Villavicencio y Jesús López Pérez*
* Instituto Nacional de Estadística y Geografía, franciscoj.corona@inegi.org.mx y jesus.lopezp@inegi.org.mx, respectivamente.

Nota: nuestro agradecimiento a Juan Martínez, Liliana Martínez y Oziel Martínez de la Dirección de Estudios Econométricos del INEGI por su valiosa orientación en el desarrollo de este trabajo; también se agradecen los comentarios de Gerardo Leyva, director general adjunto de Investigación del INEGI, por varias conversaciones sobre el tema.

 

Vol. 12, Núm. 1 – Epub                                      Inclusión del calendario mexicano…  – Epub

En este trabajo se presenta una alternativa para desestacionalizar series de tiempo económicas mexicanas utilizando, en la etapa de ajustes previos del paquete X-13ARIMA-SEATS, fechas movibles del calendario mexicano, como el Día del Trabajo, la Independencia de México y la interacción que existe entre Semana Santa con el natalicio de Benito Juárez. Se ejemplifican los resultados para el Indicador Global de la Actividad Económica (IGAE) y sus tres grandes actividades económicas. Se concluye que las variables del calendario mexicano son estadísticamente significativas para el IGAE y para las actividades terciarias, de tal forma que los resultados obtenidos indican que, en los meses donde ocurren estos eventos movibles de la economía mexicana, las variaciones mensuales difieren a las publicadas de manera oficial. De esta forma, se recomienda al INEGI evaluar la utilización del calendario mexicano en la etapa de ajustes previos en el proceso de desestacionalización para las series de tiempo económicas más relevantes. Palabras clave: ajustes previos; calendario mexicano; eventos movibles; Indicador Global de la Actividad Económica; X-13ARIMA-SEATS.

This paper presents an alternative to deseasonalize Mexican economic time series using, in the prior-adjustment stage of the X-13ARIMA-SEATS package, movable dates of the Mexican calendar, such as Labor Day, Mexican Independence Day and the interaction between Easter Week and the birth of Benito Juárez. The results are exemplified for the Global Indicator of Economic Activity (IGAE) and its three main economic activities. It is concluded that the Mexican calendar variables are statistically significant for the IGAE and for the tertiary activities, in such a way that the results obtained indicate that, in the months where these mobile events of the Mexican economy occur, the monthly variations differ from those published officially. Thus, it is recommended that INEGI evaluate the use of the Mexican calendar in the stage of previous adjustments in the deseasonalization process for the most relevant economic time series. Key words: prior-adjustments; Mexican calendar; moving holidays; Indicador Global de la Actividad Económica; X-13ARIMA-SEATS.

Recibido: 10 de octubre de 2019.
Aceptado:  22 de septiembre de 2020.

 

Introducción

En 1983, el Banco de México inició un proyecto formal y sistemático para realizar la desestacionalización de series de tiempo económicas para algunas variables relevantes del país (ver Guerrero, 1990 y 1992). En la actualidad, este proceso lo realiza de forma oficial el Instituto Nacional de Estadística y Geografía (INEGI) usando el procedimiento que otorga el programa X-13ARIMA-SEATS.^[1] Asimismo, para las variables más relevantes de la coyuntura económica, como el Producto Interno Bruto (PIB) o el Indicador Global de la Actividad Económica (IGAE), la desestacionalización se realiza con el consenso del Banco de México y las secretarías de Hacienda y Crédito Público y de Economía. Como es sabido, el objetivo del ajuste estacional es proporcionar información libre de fenómenos temporales regulares, relacionados con la periodicidad o frecuencia de las series, de tal forma que, una vez modelados y ajustados dichos fenómenos, estas reflejen solo los efectos que pueden ser aludidos a políticas económicas.

En consecuencia, los analistas de información prefieren estudiar el comportamiento de series de tiempo desestacionalizadas por diferentes motivos; por ejemplo, en el contexto de pronósticos, suele ser conveniente que las variables estén desestacionalizadas para mejorar la precisión del modelo, evitando modelar datos atípicos o estructuras temporales que puedan afectar la estimación de modelos multivariados como componentes principales; ver, por ejemplo, los trabajos recientes de Elizondo (2019) y Gálvez-Soriano (2020). Por otro lado, los economistas dedicados al análisis de coyuntura prefieren trabajar con ellas para tener mayor certeza de aspectos estructurales de corto plazo (Banco de España, 2002). Además, para aquellos agentes que toman decisiones, quienes enfrentan un shock y observan una serie con una componente estacional y otra no estacional fijarán su variable de control en la segunda de una forma que esta refleje la primera (Cochrane, 2005). Por tal motivo, mientras mejor sea la calidad del ajuste estacional, mejores elementos de decisión se proveen a los usuarios y analistas de información.

Aunque el procedimiento dentro del contexto del programa X-13-ARIMA-SEATS consta de una variedad de análisis y uso de técnicas estadísticas (resumidos más adelante), podemos centrarnos en dos pasos: 1) especificación y estimación del modelo ARIMA y 2) selección y utilización de filtros estacionales. En el primero, es relevante aislar los efectos del calendario, como la frecuencia de los días-calendario, la Semana Santa (SS), los años bisiestos, valores atípicos u outliers, entre otros; una vez modelados estos, se especifica el modelo ARIMA, donde es importante verificar los supuestos de parsimonia y la no presencia de autocorrelación serial y estacionalidad residual en los errores. En la segunda fase se realiza la selección y utilización de filtros estacionales que permiten extraer las series de tendencia-ciclo y los factores estacionales, los cuales coadyuvan a evaluar la calidad estadística del proceso de desestacionalización y, en consecuencia, obtener la serie ajustada por estacionalidad.

Enfatizando en la etapa de ajustes previos, es claro que, para el calendario gregoriano, los días-calendario, la SS y los años bisiestos son indistintos entre los países, motivo por el cual pueden ser aplicados de manera homogénea, sin importar el país al cual nos referimos. Más aún, es claro que, si en una nación las festividades son fijas, es decir, si siempre ocurren en el mismo día del mes, sus inclusiones como variables exógenas son irrelevantes al modelo ARIMA.

Para el caso de México, existe la particularidad de que, antes del 2006, los días inhábiles aludidos a eventos particulares en el país eran movibles, situación que cambió a partir de dicho año, donde se volvieron fijos, con excepción del Día del Trabajo (DT), que se presenta el 1 de mayo, y el de la Independencia de México (IM), que ocurre el 16 de septiembre. Asimismo, aunque el natalicio de Benito Juárez (BJ) es una festividad fija (tercer lunes de marzo), este puede caer en la misma semana que SS (BJ-SS), situación que, de forma tentativa, es posible que tenga un efecto en la economía, pues podría convertirse en un alargamiento vacacional o, incluso, resultar irrelevante, pues el descanso es absorbido por las vacaciones escolares de primavera.

En este trabajo se presenta un exhaustivo análisis estadístico que estudia el hecho de incluir estas particularidades del calendario mexicano en el proceso de desestacionalización, ejemplificando su aplicación para el IGAE y sus tres grandes actividades económicas (GA), el cual permite generar el precedente de análisis de esta problemática en el contexto de series económicas mexicanas. La Oficina Europea de Estadística (Eurostat, 2015, 13) recomienda que, cuando se detecten efectos derivados de festividades movibles y cuyos efectos no sean despreciables, se trate de corregirlos o calcular y remover las estimaciones de sus efectos.

Antecedente a esta investigación, para el caso de Estados Unidos de América (EE. UU.), es el de Findley et al. (2005), quienes analizaron las capacidades del X-12-ARIMA para detectar el efecto de Semana Santa en series de tiempo sintéticas; encontraron que cuatro años de información son suficientes para la identificación de impactos grandes y moderados entre 0.08 y 0.03, mientras que se requieren al menos ocho años para detectar los más pequeños, menores a 0.01. Por su parte, Roberts et al. (2010) compararon cómo se ajusta el efecto de días laborales y festivos en los paquetes X-12-ARIMA y el método de la Eurostat (inmerso en el paquete Demetra) utilizando herramientas de análisis espectral; los resultados favorecieron, en general, al de Eurostat. Otra aplicación es la que hicieron Sarhani y Afia (2014) para analizar el efecto de festividades islámicas en Marruecos, para lo cual utilizaron el criterio de información de Akaike para seleccionar entre diferentes modelos estimados con el paquete X-13ARIMA-SEATS; en particular, encontraron que, para las actividades de transporte, el efecto previo a las festividades es de solo un día, mientras que para el consumo, este se afecta desde una semana antes. En fecha reciente, en otro trabajo relacionado, McElroy et al. (2018) analizaron los efectos de festividades movibles en series de tiempo de frecuencia diaria para EE. UU.; los días feriados que se probaron fueron Pascua, Black Friday, Cyber Monday, Labor Day, domingo de Super Bowl y año nuevo chino, utilizando modelos estructurales con componentes estocásticas; encontraron que la inclusión de estos nuevos regresores permitió una modelación superior en algunos casos.

No obstante, para el caso de México —con excepción del trabajo de Guerrero et al. (2018), que analiza el efecto de las interacciones entre días-calendario con SS, concluyendo que dicha interacción es significativa para los meses de abril en el IGAE—, no hay un estudio que analice, en particular, las fechas movibles en el calendario mexicano en el proceso oficial de desestacionalización.

Se presume que el lector de este trabajo conoce la notación de los modelos ARIMA, así como que está familiarizado con conceptos esenciales básicos de desestacionalización de series de tiempo; no obstante, en caso de requerir un acercamiento introductorio al tema, se invita a revisar, por ejemplo, a Heath (2012), Guerrero et al. (2018) y el manual de referencia del programa X-13ARIMA-SEATS que provee el US Census Bureau (2020) para conocer más detalles sobre la notación y los conceptos que aquí se discuten.

Lo que resta de este documento está organizado como sigue: la sección dos presenta las generalidades del procedimiento del ajuste estacional en el contexto del X-13ARIMA-SEATS; la tercera muestra con detalle la aplicación de los métodos descritos usando el IGAE y sus tres GA; por último, en la cuarta se incluyen las conclusiones y recomendaciones.

Desestacionalizando series de tiempo con X-13ARIMA-SEATS

El procedimiento de ajuste estacional dentro del programa X-13ARIMA-SEATS es la evolución del método inicialmente desarrollado por el Census Bureau de EE. UU., conocido como Census Method II, el cual progresó a X-11 y, con el tiempo, a X-12-ARIMA. El X-13ARIMA-SEATS es utilizado por una gran cantidad de países en el mundo, sobre todo en América. A continuación, se hace un breve recuento de esta metodología.

Series de tiempo: aditivas y multiplicativas

Se define que la serie de tiempo de periodicidad mensual o trimestral ( Y_t, para t = 1,…,N) está compuesta por una componente de tendencia-ciclo (T_t), que incluye los movimientos a largo plazo de la serie y las fluctuaciones económicas no atribuibles a su periodicidad y sí a eventos económicos relevantes, como pueden ser políticas gubernamentales; la estacionalidad (E_t), que incluye los efectos calendario y la dinámica relacionada con su periodicidad; y la irregularidad (I_t), que representa la componente aleatoria, es decir, no atribuible a factores de índole estructural, motivo por el cual se le aíslan posibles outliers, cambios de nivel, etcétera.

En consecuencia, la serie de tiempo puede ser aditiva, si la suma de las componentes T_t,E_t e I_t generan a Y_t, o multiplicativa si es atribuible al producto de estas. Representaciones híbridas pueden verse en Dagum (1980), Findley et al. (1998) y Ladiray y Quenneville (2000-2001).

En el contexto del programa X-13ARIMA-SEATS solo hacemos referencia a series aditivas o multiplicativas, de tal forma que cuando son del segundo tipo, se pueden aplicar logaritmos a Y_t, transformándolas en aditivas. Para diagnosticar lo anterior, se puede consultar un gráfico, de tal manera que, si el patrón estacional no varía a través del tiempo, se relaciona con una estacionalidad aditiva; por otra parte, si este va cambiando, se suele decir que la serie es multiplicativa. Existen pruebas formales para concluir sobre el carácter aditivo o multiplicativo de la serie, por ejemplo, la automática que porta el paquete X-13ARIMA-SEATS, que está basada en los criterios de Akaike y pruebas de transformación-potencia (ver Guerrero, 1993).

Especificación y estimación del modelo regARIMA

En la etapa de ajustes previos buscamos tener una serie ajustada  por efectos del calendario y disrupciones en esta. Para ello, se utiliza un modelo de regresión con errores ARIMA (regARIMA), es decir, donde la función se describe por una combinación lineal de regresores (x) y la estructura de la covarianza es la de un proceso ARIMA:

ϕ(B)Φ(B^S ) (1 – B)^d (1 – B^S )^D (y_t – ∑_i β_ix_it) = θ(B)Θ(B^S) a_t.                   (1)

Note que, si no se emplea ningún regresor, el regARIMA se reduce a uno ARIMA.

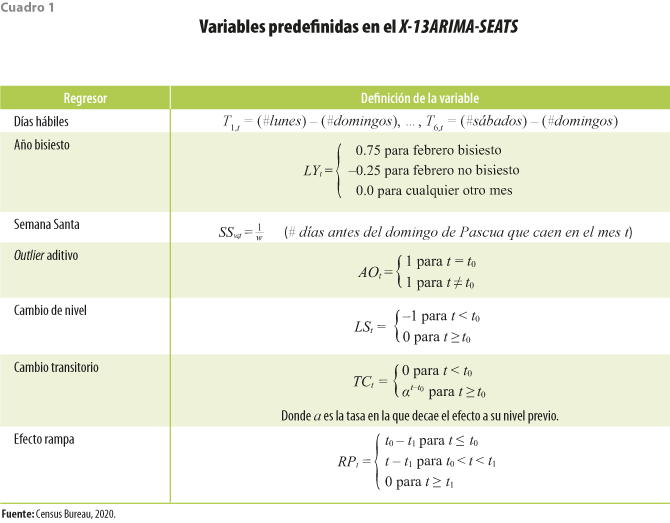
El programa X-13ARIMA-SEATS tiene ya implementados diversos regresores para estimar y aislar los efectos de calendario, por ejemplo: días hábiles (TD por Trading Days), año bisiesto (LY por Leap Year) y de festividades movibles (como SS para la Semana Santa). También, hay otros regresores para ciertos tipos de disrupciones en las series (outliers), los cuales se pueden clasificar como aditivos (AO por Additive Outlier); de cambio permanente de nivel (LS por Level Shift), cuyo efecto se mantiene una vez que aparece y se representan mediante una función de escalón; de cambio transitorio (TC por Transitory Change), que una vez que ocurren muestran un patrón de absorción en la serie y desaparecen a la larga; y de efecto rampa (RP por Ramp).

La forma como se construyen e introducen estas variables en la ecuación (1) se muestra en el cuadro 1.

Además de las variables aquí mostradas, el modelo regARIMA en el paquete X-13ARIMA-SEATS permite incorporar otras opciones predefinidas o bien otras definidas por el usuario. En este trabajo se utiliza la expresión (1) para incorporar los efectos de calendario que deseamos probar (en específico DT, IM, BJ-SS), lo cual se detalla en la tercera sección.

Una vez determinados los efectos de calendario, se sigue la metodología de Box y Jenkins (1970) para la construcción del modelo ARIMA, analizando las funciones de autocorrelación y de autocorrelación parcial, de tal forma que el ajuste de este incluya el número de diferencias para que la serie de tiempo sea estacionaria, posibles diferencias estacionales, el orden de parámetros autorregresivos y de medias móviles, tanto para el nivel de la serie como para la componente estacional no estable.

En esta fase se suele evaluar, además, que los coeficientes del modelo ARIMA sean significativos y, sobre todo, que el residuo obtenido no presente autocorrelación serial ni estacionalidad residual, lo cual implica estimaciones parsimoniosas y óptimas desde el punto de vista estadístico. Lo obtenido en la etapa de ajustes previos, aquí es crucial para realizar pronósticos hacia atrás y hacia adelante, que permiten, en la etapa siguiente, aplicar los filtros estacionales.

Filtros estacionales

Para estimar las componentes de las series de tiempo ( T_t, E_t  e I_t ), se aplican filtros estacionales de medias móviles a la serie  . Los filtros de tendencia son promedios ponderados de meses o trimestres consecutivos utilizados para estimar T_t; por otra parte, los estacionales consisten en medias móviles estacionales de valores consecutivos dentro de un mes o trimestre determinado. Una media móvil  n × m es un promedio simple de m términos tomada en n tramos secuenciales consecutivos. De esta forma, se usan esos filtros para estimar la componente asociada a E_t.

El uso de los filtros es iterativo, suponiendo que la serie de tiempo sigue una estacionalidad aditiva, en la primera etapa se obtiene una estimación inicial de la tendencia usando filtros de tendencia para Y_t, obteniendo, así, T_t⁽¹⁾. En consecuencia, se estima la componente inicial de estacionalidad-irregularidad como EI_t⁽¹⁾ = Y_t – T_t⁽¹⁾. Después, usando filtros estacionales para EI_t⁽¹⁾, se obtiene una primera estimación del factor estacional (EI_t⁽¹⁾), de tal manera que el ajuste estacional inicial es A_t⁽¹⁾ = Y_t – E_t⁽¹⁾. En el siguiente paso, el proceso se reinicia usando A_t⁽¹⁾ y el filtro de Henderson para obtener una nueva estimación de la tendencia, de tal forma que, iterando el proceso un paso más para estimar la tendencia, la descomposición final de la serie de tiempo es:

donde ,,.  El criterio para la selección de la media móvil estacional se basa en la Î/Ê global, que mide el tamaño relativo de los movimientos irregulares y los estacionales promediados durante todos los meses o trimestres.

El criterio empírico para determinar si el filtro estacional es adecuado se muestra en el cuadro 2.

 

Resumen de desestacionalización de series de tiempo económicas

Una vez descritas las generalidades del procedimiento de desestacionalización usando el X-13ARIMA-SEATS, los siguientes son los pasos para hacerlo:

1. Revisar patrones gráficos tanto para la serie original como en logaritmos: tendencias, posible tipo de estacionalidad, presencia cambios estructurales, etcétera.
2. Estimar el modelo automático para diagnosticar si la serie es candidata para desestacionalizarse, las diferencias sugeridas (integración) y el tipo de estacionalidad indicada (aditiva o multiplicativa). De manera alternativa, se puede usar una prueba de raíces unitarias para diagnosticar, en su caso, el tipo de transformación estacionaria y el criterio de Guerrero (1993) para identificar el tipo de estacionalidad.
3. Aplicar algún criterio estadístico complementario para definir si la serie presenta estacionalidad, por ejemplo, el estadístico M7 (Lothian y Morry, 1978) o la prueba de estabilidad residual, D8-F.
4. Analizar si las variables de frecuencia de días-calendario (SS y LY) son significativas en el regARIMA. De forma alternativa, se puede explorar el uso de otras variables exógenas relevantes, por ejemplo, los eventos movibles específicos del país, como se hace en el presente trabajo.
5. Analizar la existencia de outliers.
6. Identificar el modelo ARIMA a través de la metodología Box-Jenkins. Estimar el modelo evaluando los siguientes criterios:
   1. Significancia de parámetros: omitir la presencia de términos no significativos a través de pruebas de significancia conjunta.
   2. No autocorrelación ni heterocedasticidad condicional en los residuos: pruebas Ljung-Box y efecto ARCH.
   3. Normalidad de los residuales: pruebas Shapiro-Wilk y Jarque-Bera, entre otras. Este punto puede omitirse argumentando que la distribución asintótica de los estimadores por máxima verosimilitud es consistente en el límite.
   4. Estacionariedad en el modelo ARIMA.
   5. Baja correlación de los parámetros en el modelo ARIMA.
   6. Estudiar la capacidad predictiva del modelo fuera de muestra, esto dado que en la etapa de aplicación de filtros estacionales se requiere extender la serie hacia atrás y hacia adelante.
7. Aplicar las pruebas explicadas en el punto 2 a los residuales del modelo ARIMA.
8. Seleccionar los filtros estacionales de acuerdo con el cuadro 2 y aplicar estos para obtener las componentes de la serie de tiempo.
9. Revisar la consistencia de los resultados en términos estructurales: variaciones mensuales, trimestrales y anuales concordantes a través del tiempo.
10. Decidir si para los agregados se debe aplicar el método directo o el indirecto de desestacionalización.

Note que los efectos de eventos-calendario movibles considerados en el punto 4 se mantienen fijos dentro de un trimestre, por lo que no afectan a las series trimestrales. Solo el efecto de Semana Santa puede ocurrir en el primer o segundo trimestres. En relación con el punto 10, es importante señalar que la desestacionalización que realiza el INEGI es de manera directa, es decir, el agregado es desestacionalizado sin importar sus desagregados. Lo anterior tiene su justificación en el hecho de que, al hacerlo de esta forma, se puede garantizar la optimalidad estadística en todo el proceso de desestacionalización (Eurostat, 2015), situación que, de manera indirecta, agregando las componentes a través de sumas, no se puede verificar de forma estadística. En ese sentido, la Eurostat también señala que, cuando se utiliza el método indirecto, es más recomendable incorporar los efectos de calendarios nacionales.

Desestacionalización del IGAE y sus componentes

Para desestacionalizar las series de tiempo mensuales del IGAE y sus tres GA (GA1: actividades primarias; GA2: secundarias y GA3: terciarias), para el periodo de enero de 1993 a julio de 2019, usamos los modelos utilizados de manera oficial por el INEGI.^[2]

En este trabajo se considera que las variables incluidas en los modelos INEGI para la etapa de ajustes previos de días hábiles, año bisiesto, Semana Santa, outliers o los órdenes ARIMA han sido determinados con rigurosidad estadística, lo que valida su implementación y sus resultados, y sobre estos se adicionan las variables de interés en esta investigación (DT, IM y la interacción BJ-SS). Lo anterior brinda comparabilidad respecto a las series que fueron publicadas en su oportunidad.

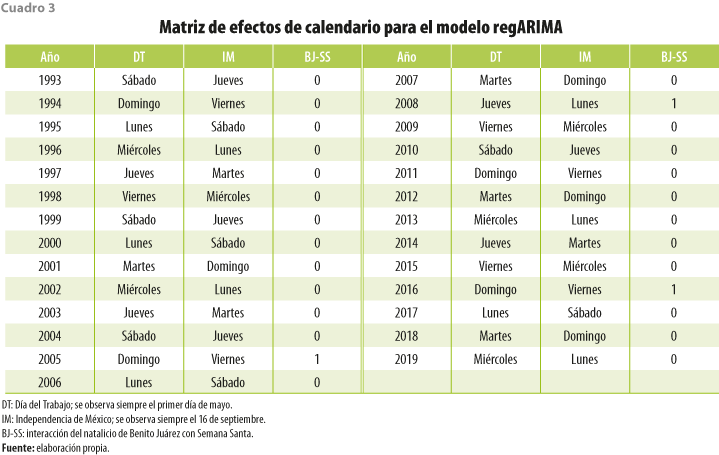
La manera en que se incorporan los efectos de calendario del DT y la IM es descontándolos de la variable TD, como se definió en el cuadro 1. Por ejemplo, el DT en 1993 ocurrió en sábado, por lo que se descontaría ese día para contabilizar solo cuatro en lugar de cinco sábados de actividad económica para ese mayo; de la misma manera, el IM de ese año fue jueves, con lo que tendríamos tres y no cuatro jueves con actividad económica para septiembre. Con respecto a la interacción BJ-SS se incluye como variable exógena de la siguiente manera:

   

El cuadro 3 muestra la ocurrencia de estas fechas para el periodo de análisis.

 

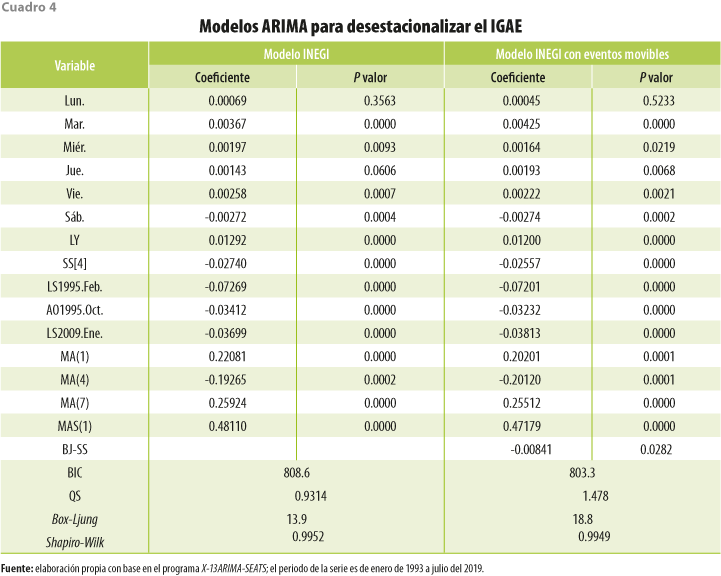
Para el caso del IGAE, los resultados de los modelos (el publicado de manera oficial y el obtenido al incluir los eventos movibles del calendario mexicano) se resumen en el cuadro 4.

Se puede apreciar que, a 5 % de significancia, el coeficiente BJ-SS es significativo, además de que los jueves se vuelven significativos respecto al modelo utilizado de forma oficial por el INEGI. Los demás coeficientes mantienen su interpretabilidad estadística. En los análisis de los modelos, en ambos casos, no existe ni estacionalidad residual ni autocorrelación serial según las pruebas QS y Ljung-Box, respectivamente. También, los residuales se comportan de manera normal de acuerdo con la prueba Shapiro-Wilk. Es de interés mencionar que el BIC o criterio bayesiano es menor para el modelo que incluye las variables del calendario mexicano, lo cual indicaría que es más informativo respecto al que no las incluye. Aunque los modelos no son totalmente anidados, dado que la frecuencia de los días-calendario no es la misma entre modelos, a manera descriptiva (realizando una razón de verosimilitudes) concluimos que el p valor es 0.00, motivo por el cual rechazamos la hipótesis nula de que ambos modelos son igual de informativos; es decir, tenemos argumentos para concluir que el modelo que incluye los eventos movibles del calendario mexicano es más informativo.

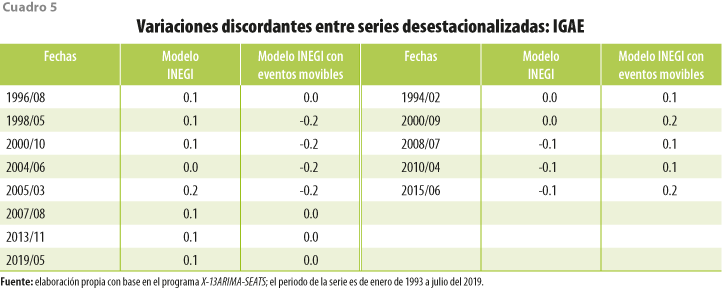
Es importante analizar las variaciones mensuales discordantes entre ambos modelos, es decir, cuando las variaciones de las series desestacionalizadas oficialmente difieren del modelo alternativo. El cuadro 5 presenta los resultados: del lado izquierdo, aquellas con las que el modelo INEGI con eventos movibles arrojó discordancias cero o negativas y del lado derecho, las positivas.

Podemos apreciar que las series desestacionalizadas otorgan un total de 13 variaciones discordantes, de las cuales 10 son positivas y tres, negativas para el modelo INEGI, mientras que, cuando se incluyen eventos movibles del calendario mexicano resultan nueve positivas y cuatro negativas. Llama la atención analizar que la mayoría de los meses son circundantes entre marzo, mayo y septiembre, es decir, cuando se presentan los efectos BJ-SS, el DT y la IM. Estos resultados permiten identificar que, en general, la presencia de estas festividades tiende a disminuir las tasas de crecimiento, ya que, al haber menor número de días hábiles, se frena de forma ligera la actividad económica. Es conveniente comentar que estas discrepancias no pueden explicarse de manera directa a partir de los coeficientes del modelo debido a que, como hemos visto, la etapa de los filtros estacionales rompe la interpretabilidad y su principal función es extender la serie en sus extremos, situación que la metodología TRAMO-SEATS trata de evitar.

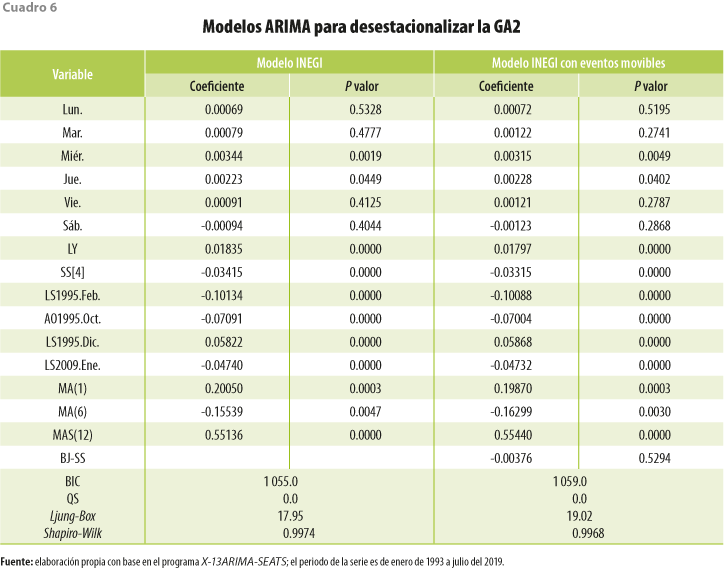
Analizando las componentes del IGAE, es importante resaltar que el modelo ARIMA de la GA1 es un ARIMA ([4] 0 [5 10 11])(0 1 1) sin variables de TD, LY y SS, motivo por el cual no es necesario modelar los eventos movibles del calendario mexicano. Para la GA2 se utiliza un modelo ARIMA (0 1 [1 6])(0 1 1). Los resultados se resumen en el cuadro 6.

Para este modelo no resulta significativa la variable BJ-SS, además de que no se gana significancia en los días-calendario. Asimismo, el BIC es menor en el modelo que no incluye los eventos del calendario mexicano. Nótese que este parece tener ciertos problemas de estacionalidad residual; no obstante, de acuerdo con el contraste de Ljung-Box, los residuales están libres de autocorrelación serial, además de que estos se comportan de manera normal.

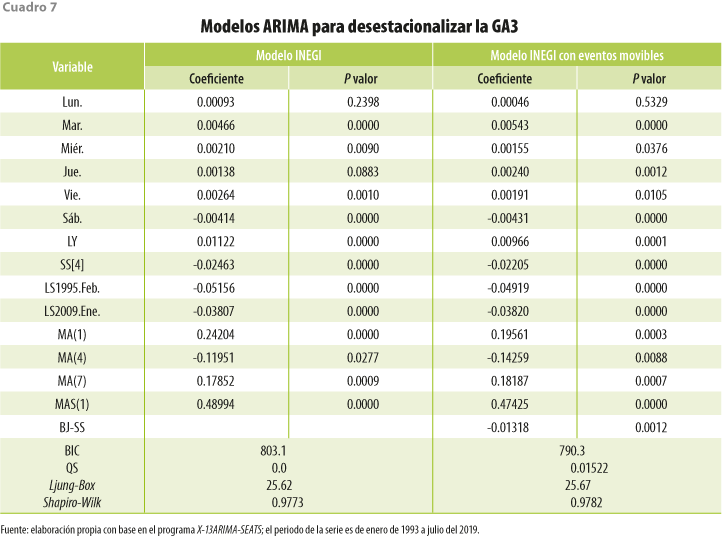
Para la GA3 se utiliza un modelo ARIMA (0 1 [1 4 7 ])(0 1 1), dado que es el sector con mayor participación en el total de la economía;^[3] son, a priori, esperables resultados similares a los del IGAE, los cuales se presentan en el cuadro 7.

De igual manera que para el IGAE, para la GA3, en el modelo que incluye los eventos movibles del calendario mexicano, hay dos términos más significativos respecto al que no las considera, los cuales son los jueves y la interacción BJ-SS y, asimismo, el BIC es menor en dicho modelo.

Por lo anterior, aunado a que ambos modelos no presentan problemas de estacionalidad residual, autocorrelación serial y no normalidad en los errores, podemos concluir que el modelo que incluye las variables del calendario mexicano es más informativo que el que no las contempla, motivo por el cual las series de tiempo tenderían a estar desestacionalizadas de mejor manera.

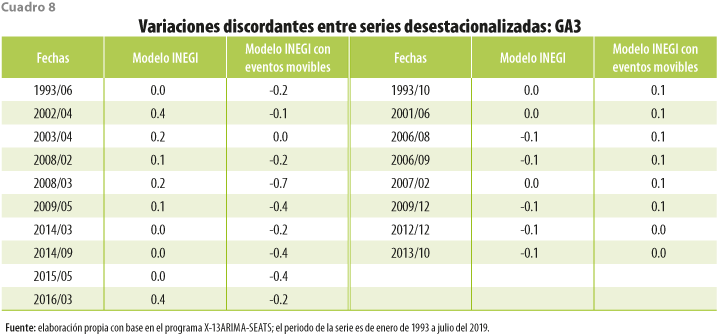
El cuadro 8 representa las discrepancias en los signos de las variaciones porcentuales mensuales de cada modelo.

 

Al igual que el IGAE, la mayoría de los meses discordantes son cercanos a aquellos donde se presentan los tres eventos movibles que se han modelado en este trabajo, donde llama la atención cómo (ligeramente) el crecimiento económico está siendo sobrevalorado que si incluyéramos las variables del calendario mexicano.

Conclusiones y recomendaciones finales

La desestacionalización de series de tiempo proporciona, al público en general, información libre de patrones contaminados por la periodicidad de estas, lo cual es importante en materia de política económica, pues permite a la sociedad conocer el impacto de las políticas sobre el tema de mejor manera. En consecuencia, es necesario que esta acción se realice con las mejores prácticas disponibles. En este sentido, el INEGI, institución encargada de desestacionalizar de manera oficial las series de tiempo, utiliza el procedimiento del programa X-13ARIMA-SEATS, verificando cada uno de los supuestos que garantizan la correcta aplicación del método.

Sin embargo, es claro que dentro del proceso de desestacionalización se pueden incluir variables exógenas en la parte de ajustes previos, en particular, eventos movibles del calendario mexicano, lo cual puede ayudar a representar, de mejor forma, series de tiempo desestacionalizadas. Este trabajo analizó el efecto de incluir, de manera conjunta, el DT, la IM y el evento BJ-SS en la desestacionalización del IGAE.

Los resultados permiten concluir que, para el IGAE y su GA3, dichos eventos son relevantes estadísticamente, ya que resultan significativos y mejora la capacidad informativa de los modelos. Las series de tiempo que incluyen estos efectos presentan, de forma ligera, tasas de crecimiento mensuales menores respecto a los modelos que no los muestran, sobre todo, en los meses circundantes a la presencia de dichos eventos movibles.

Se recomienda al INEGI analizar la viabilidad de utilizar este enfoque, si no en todas, sí en las variables más relevantes de la coyuntura económica, como pueden ser el PIB, el IGAE, el consumo privado y la inversión fija bruta, entre otras, con el fin de otorgar información desestacionalizada que presente eventos particulares de México de manera significativa y, por ende, series de tiempo desestacionalizadas con un mayor sustento estadístico.

__________________

Fuentes

Banco de España. Ajuste estacional y extracción de señales en la contabilidad nacional trimestral. Documentos de trabajo 0210. Banco de España, Servicio de Estudios, 2002.

Box, G. y G. Jenkins. Time Series Analysis: Forecasting and Control. San Francisco, Holden-Day, 1970.

Cochrane, John H. Time series for macroeconomics and finance. Manuscript. University of Chicago, 2005.

Dagum, E. B. The X-11-ARIMA Seasonal Adjustment Method. Catalogue 12-564E. Ottawa, Canada, Statistics Canada, 1980.

Elizondo, Rocío. “Estimaciones del PIB mensual en México basadas en el IGAE”, en: Estudios Económicos. 34(2), 2019, pp. 197-241.

Eurostat. ESS guidelines on seasonal adjustment. Luxembourg, Eurostat, 2015.

Findley, D. F., B. C. Monsell, W. R. Bell, M. C. Otto y B-Ch. Chen. “New capabilities and methods of the X-12-ARIMA Seasonal Adjustment Program”, in: Journal of Business and Economic Statistics. 16(2), 1998, pp. 127-152.

Findley, D., K. Wills and B. Monsell. Issues in estimating Easter regressors using RegARIMA models with X-12-ARIMA. Proceedings of the American Statistical Association, 2005.

Gálvez-Soriano, Oscar de J. “Nowcasting Mexico’s quarterly GDP using factor models and bridge equations”, en: Estudios Económicos. 35(2), 2020, pp. 213-265.

Guerrero, V. M. “Desestacionalización de series de tiempo: una introducción a la metodología”, en: Comercio Exterior. 40(11), 1990, pp. 1035-1046.

______ “Desestacionalización de series de tiempo económicas: ajustes previos”, en: Comercio Exterior. 42(11), 1992, pp. 1042-1053.

______ “Time‐series analysis supported by power transformations”, en: Journal of Forecasting. 12(1), 1993, pp. 37-48.

Guerrero, V. M., J. López-Pérez y F. Corona. “Ajuste estacional de series de tiempo económicas en México”, en: Realidad, Datos y Espacio Revista Internacional de Estadística y Geografía. 9(3), 2018, pp. 74-97.

Heath, Jonathan. Lo que indican los indicadores. Cómo utilizar la información estadística para entender la realidad económica de México. México, INEGI, 2012.

Ladiray, D. y B. Quenneville. “Desestacionalizar con el método X-11”, en: METHODOLOGICA. Número especial, núm. 8-9. Bruxelles, Belgique, Universite Libre de Bruxelles, 2000-2001.

Lothian, J. y M. Morry. A Set of Quality Control Statistics for the X11-ARIMA88 Seasonal Adjustment Method. Working Paper, 78-10-005, 1978.

Lothian, Jack. “The identification and treatment of moving seasonality in X-11ARIMA”, in: Proceedings of the Business and Economic Statistics Section of the American Statistical Association. 1984, pp. 166-171.

McElroy, Tucker. S., Brian C. Monsell y Rebecca. J. Hutchinson. Modeling of holiday effects and seasonality in daily time series. Reporte técnico. Center for Statistical Research & Methodology Research and Methodology Directorate U.S. Census Bureau, 2018.

Roberts, Christopher G., Scott H. Holan y Brian C. Monsell. “Comparison of X-12-ARIMA Trading Day and Holiday Regressors with Country Specific Regressors”, in: Journal of Official Statistics. 26(2), 2010, pp. 371-394.

Sarhani, M. & A. El Afia. “An extension of X13-ARIMA-SEATS to forecast islamic holidays effect on logistic activities”, in: 2014 International Conference on Logistics Operations Management. IEEE, 2014 June, pp. 79-84.

Sax, C. y D. Eddelbuettel. “Seasonal Adjustment by X-13ARIMA-SEATS”, in: R. Journal of Statistical Software. 87(11), 2018, pp. 1-17.

US Census Bureau. X-13ARIMA-SEATS. Reference Manual. 2020.

^[1] ARIMA hace referencia a Modelos Autorregresivos, Integrados de Medias Móviles y SEATS, a Seasonal Adjustment by Signal Extraction.

^[2] https://bit.ly/2Q8mYJr

^[3] Para el 2019, la GA1 representaba 3 %; la GA2, 30 %; y la GA3, 67 % del total del PIB.