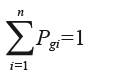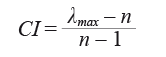Toma de decisiones en ambientes de salud: modelos de jerarquización analítica de alternativas para la vacunación en México

Decision-making in Health Care Settings:
Analytical Ranking Models for Vaccination Alternatives in Mexico

 

Mario Gutiérrez Lagunes
Universidad Autónoma de San Luis Potosí, mario.gutierrez.lagunes@uaslp.mx

 

Vol. 13, Núm. 3 de 2022 – EPUB                                         Toma de decisiones… – EPUB

El Proceso Analítico Jerárquico (AHP, por sus siglas en inglés) es un procedimiento de toma de decisiones utilizado en la asignación de prioridades en problemas de decisión multicriterio. Ante la urgencia de vacunación que se presenta en algunos países, la aplicación de la metodología del AHP aporta confianza en nuestras decisiones en términos de la teoría moderna de la medición. El objetivo de este trabajo es, aplicando el esquema del AHP, evaluar el uso y la pertinencia de vacunación masiva en un ambiente de urgencia por combatir el COVID-19. El análisis y la jerarquización de los criterios para vacunar y los estados de vulnerabilidad con respecto a la salud con estas variables se utilizaron para crear matrices de comparación pareadas. La razón de consistencia entre las decisiones pareadas fue de 0.0114; se concluye que la construcción de estas matrices para analizar y evaluar objetivamente la jerarquización presentada fue consistente. Palabras clave: proceso analítico jerárquico; teoría de decisiones; matriz de comparación; COVID-19. Clasificación JEL: C44, C44, C6, I1.

The Analytic Hierarchical Process (AHP) is a decision-making procedure used in assigning priorities in multi-criteria decision problems. Given the urgency of vaccination in some countries, the application of the AHP methodology provides confidence in our decisions in terms of modern measurement theory. The objective of this work is, by applying the AHP scheme, to evaluate the use and relevance of mass vaccination in an environment of urgency to combat COVID-19. The analysis and ranking of criteria for vaccination and health vulnerability states with these variables were used to create paired comparison matrices. The consistency ratio between the paired decisions was 0.0114; it is concluded that the construction of these matrices to objectively analyze and evaluate the ranking presented was consistent. Key words: hierarchical analytical process; decision theory; comparison matrix; COVID-19.

 

Recibido: 30 de abril de 2021
Aceptado: 18 de febrero de 2022

 

Introducción

A raíz de la crisis provocada por la pandemia a inicios del 2020, y ante la limitada y retardada llegada de la vacuna contra el COVID-19 para la mayoría de los países con el fin de procurar la salud de sus habitantes lo antes posible, casi todos los gobiernos se han encontrado en apremio de mitigar esta contingencia que no cesa. De acuerdo con el informe publicado por Oxfam Novib (OXFAM, 2021), se tiene que la desigualdad entre las naciones es más notoria a nivel global, donde se indica que para el selecto mundo de los mil hombres más ricos del mundo les lleva solo nueve meses recuperar su riqueza previa a la pandemia, en cambio, a las personas más marginadas les llevará, probablemente, más de 10 años superar las consecuencias económicas propias de esta emergencia sanitaria, por lo que la aparición de nuevos pobres es un efecto de esta crisis, siendo las mujeres y los grupos minoritarios los más perjudicados.

Por otro lado, el esfuerzo del gobierno mexicano para garantizar el acceso a las vacunas con las principales farmacéuticas mundiales —como Pfizer (Estados Unidos de América-Alemania), Astra Zeneca (Gran Bretaña) y CanSino (China), entre otras— se ha visto limitado por la escasez de estas debido, principalmente, por el acaparamiento por parte de los países más ricos, por lo que ha ampliado su estrategia de la obtención de las vacunas a la brevedad posible.

Para lograr existencias que cubran de forma gratuita a toda la población mexicana, el gobierno tuvo que firmar acuerdos de confidencialidad con las farmacéuticas. Desde el inicio de la vacunación (el 24 de diciembre de 2020), hasta el 31 de octubre de 2021, se han aplicado poco más de 126 millones de vacunas, contando con el esquema completo de vacunación contra el COVID-19 81 % de la población (Gobierno de México, 2021). El total de dosis recibidas ha sido de 153 280 045, iniciando por la población que está en el sector salud y, después, por la más vulnerable, enfocándose en los adultos de 60 años y más de edad. Todavía falta mucho por atender para que se logre la inmunidad de este sector, pero la mayor disponibilidad de personal sanitario, ya vacunados, hace pensar que los enfermos están mejor atendidos hoy en comparación con hace algunos meses.

El objetivo de este estudio empírico es evaluar, bajo el Proceso Analítico Jerárquico (AHP, por sus siglas en inglés), el uso y la pertinencia de vacunación masiva en un ambiente de urgencia para combatir el COVID-19, calculando un vector de jerarquización de las decisiones a realizar sujeto a un índice de consistencia.

La estructura del trabajo es como sigue: primero se presenta una introducción del panorama de la crisis por la escasez de vacunas para combatir el COVID-19 en el mundo, así como la situación en México; enseguida se exponen los criterios, los principios y la vulnerabilidad que se tiene frente al virus SARS-CoV-2 de acuerdo con los Centros para el Control y la Prevención de Enfermedades (CDC, por sus siglas en inglés, 2021) y el grupo técnico asesor para la vacuna en México, así como la distribución de la población de adultos mayores de 60 años y más en el país; después, se explica la metodología del AHP para su aplicación en este trabajo; posteriormente, se analizan los resultados obtenidos de la metodología propuesta en la aplicación de la vacuna; y, por último, se muestran las conclusiones de los hechos más importantes encontrados en esta investigación enfocada a la toma de decisiones resultante.

 

Criterios

El proceso de desarrollo de la vacuna contra COVID-19 es arduo y complejo: pasar por fases de ensayos clínicos y ser aprobada por instancias nacionales e internacionales para garantizar su eficacia, seguridad y efectividad. Por otra parte, la estrategia de vacunación enfrenta otros retos, como el manejo, la distribución y la administración de las vacunas, ante la escasez de estas.

Para ello, la Organización Mundial de la Salud (OMS) ha establecido un marco de valores del Grupo de Expertos en Asesoramiento Estratégico (SAGE, por sus siglas en inglés) sobre Inmunización (WHO, 2020). Los seis principios que guían a que las vacunas contra el COVID-19 deben ser un bien público mundial son: bienestar humano, respeto igualitario, equidad mundial y nacional, reciprocidad y legitimidad. Asimismo, tiene como objetivo ofrecer orientación a nivel mundial acerca de la asignación de las vacunas contra  el COVID-19 entre las naciones, así como orientar a nivel nacional acerca de la determinación de los grupos prioritarios para recibirlas dentro de los países, en especial cuando el suministro es limitado. Cabe hacer mención que este marco solo está diseñado para abordar los aspectos éticos relacionados con la asignación y priorización de estas vacunas, dejando fuera del alcance el diseño de los ensayos y el proceso regulatorio.

De acuerdo con la Política Rectora de Vacunación (PRV) contra el COVID-19 (Cortés et al., 2021), el Grupo Técnico Asesor para la Vacuna (GTAV) COVID-19 en México (formado por expertos en materia de inmunología, vacunación, infectología, sociología, sistemas y economía de la salud) ha recomendado llevar a cabo una estrategia enfocada en reducir el número de muertes asociadas con la enfermedad, diseñada con base en la mortalidad observada en México y apoyada por el Instituto Nacional de Salud Pública, el cual realizó un análisis de la información nacional e internacional, así como la revisión de diversos estudios relacionados con los riesgos de salud, pobreza e inequidad con respecto a la infección y muerte por COVID-19.

Así, acorde con las recomendaciones del GTAV, los cuatro ejes de priorización para la vacunación contra el virus SARS-CoV-2 en México se pueden apreciar en el cuadro 1.

Una vez establecidas estas prioridades de vacunación, anunciadas en la PRV por Cortés et al. (2021), se espera reducir el número de personas fallecidas por COVID-19 en México. El eje de priorización 1, Edad de las personas, es el principal, con énfasis en vacunar prioritariamente dentro de cada grupo etario a quienes viven con comorbilidades En particular, algunas de las que padecen aquellos que vayan a recibir la vacuna tienen un componente personal de control, ya que muchas de las personas que viven con diabetes, hipertensión o VIH tienen sus condiciones controladas, las cuales ayudan a reducir el riesgo específico. En cuanto a los grupos de atención prioritaria, como individuos con discapacidad y la niñez, entre otros, todavía no cuentan con una autorización de uso en emergencia a nivel mundial. Con respecto al eje de priorización de la vacunación, el comportamiento de la epidemia es dinámico, donde cada entidad federativa tiene diversas epidemias hacia el interior de su territorio, además de que estas afecciones locales dependen también de diferentes factores, el más importante epidemiológicamente hablando es la densidad poblacional.

 

Vulnerabilidad

De acuerdo con los CDC (2021), los adultos mayores y los grupos de cualquier edad con afecciones subyacentes graves son las personas más vulnerables y con un mayor riesgo de enfermarse gravemente a causa de COVID-19, sin embargo, existen más grupos de individuos que también lo son a este virus.

Los expertos en salud han hecho una lista de las personas más vulnerables ante COVID-19 y que, por lo tanto, deben tener mayores cuidados para reducir el riesgo de presentar complicaciones graves. Las presentadas en la PRV se observan en el cuadro 2.

 

Con las características asociadas con un mayor riesgo de morir por COVID-19, se establece la estrategia de contención de defunciones donde se propone una priorización de grupos poblacionales a vacunar. Con base en los datos del Sistema Nacional de Vigilancia Epidemiológica, el GTAV hizo un análisis de mortalidad por grupo de edad en México, donde se encontró que los de 65 a 69 y 60 a 64 años eran los que alcanzaban los mayores porcentajes de mortalidad y los de 0 a 19 y 20 a 24 eran los que presentaban los menores valores. Con los resultados de este análisis, los grupos priorizados en la orden de prelación, establecidos por el GTAV en la PRV, más detallado son:

1. Personal sanitario que enfrenta COVID-19.
2. Personas adultas mayores:
3. Mayores de 80 años.
4. de 70 a 79.
5. de 60 a 69.
6. Personas con comorbilidad o comorbilidades:
7. Obesidad mórbida.
8. Diabetes mellitus.
9. Hipertensión arterial sistémica.
10. Enfermedad pulmonar obstructiva crónica (EPOC).
11. Asma.
12. Enfermedades cerebrovasculares.
13. Infección por VIH.
14. Enfermedad renal crónica.
15. Estados patológicos que requieren de inmunosupresión.
16. Cáncer en tratamiento.
17. Personal docente de las entidades federativas en semáforo epidemiológico verde.
18. Resto de la población (mayor a 16 años de edad).

Aunque también existen otras poblaciones vulnerables a contraer COVID-19, como las mujeres embarazadas, personas sin hogar y con discapacidades, entre otras. Cabe mencionar que, por el momento, ninguna vacuna será aplicada a individuos menores de 16 años, hasta que se cuente con la suficiente evidencia de seguridad en esta población; actualmente, ningún ensayo clínico ha incluido a menores de edad y mujeres embarazadas.

Bajo este contexto, y la escasez de vacunas, las pocas que llegan, ¿a quiénes se les aplican?

Para contestar esta pregunta, se estableció la estrategia sugerida por el GTAV en la Política Rectora de Vacunación contra el COVID-19 a la población mexicana, en sus diferentes entidades, ubicando a la población de 60 años y más de edad.

 

Población de México

De acuerdo con el Censo de Población y Vivienda 2020 (INEGI, 2020), el total de habitantes de la República Mexicana es de 126 013 024, de los cuales 15 142 976 son personas de 60 años y más, es decir, 12 % de la población pertenece a este rango etario. Las cinco entidades donde se concentra cerca de 42 % de este grupo de edad son: México (12.7 %), la Ciudad de México (9.9 %), Veracruz de Ignacio de la Llave (7.6 %), Jalisco (6.6 %) y Puebla (4.9 %). En contraste, las cinco con menos adultos mayores son: Aguascalientes (0.96 %), Quintana Roo (0.87 %), Campeche (0.68 %), Colima (0.60 %) y Baja California Sur (0.50 %), donde entre todas suman 3.6 % de dicha población (ver mapa).

 

Teniendo este panorama de la distribución de los adultos de 60 años y más en la República Mexicana, y ante la urgencia de vacunar a lo más importante que posee un país, que es su gente, aunado a la escasez de vacunas, la pregunta es: ¿a quién vacunamos primero de este segmento de la población?

Por otra parte, cabe señalar que 75.7 % de la población mexicana cuenta con asistencia de un seguro médico, donde Chihuahua alcanza una cobertura de 84.4 % y Michoacán de Ocampo es el más rezagado en atención de servicios médicos, tiene 62.2 % (INEGI, 2020), por lo que la situación se vuelve más crítica por no contar con la infraestructura suficiente para una emergencia de salud como la que se ha presentado en el país y poder dar solución a la vacunación en un tiempo mínimo.

Marco teórico

El uso de la toma de decisiones se ha vuelto más frecuente debido al empleo de sistemas computacionales que permiten analizar los diferentes recursos tanto organizacionales como humanos, los cuales buscan alcanzar esquemas de optimización. Lo anterior puede ser modelado a través de representaciones formales que clarifican las relaciones entre necesidades, recursos disponibles y objetivos establecidos para alcanzar una meta. Las matemáticas, dentro de la teoría de decisiones, agrupa los criterios y decisiones que, mediante su análisis y procesamiento —cumpliendo ciertas reglas de comportamiento establecido de antemano—, alcancen el óptimo, esto es, las resoluciones más adecuadas, dando consistencia, transparencia y robustez a todo el proceso desde su fase inicial hasta la final del problema.

La aplicación de sistemas analíticos para la toma de decisiones es ampliamente utilizada por instituciones de diferente índole, desde organismos gubernamentales hasta empresas y consorcios, pues provee señales para anticipar soluciones a problemas que amenazan su supervivencia en el mercado. Puede decirse que, de manera general, los modelos de mayor aplicación comprenden una combinación de aspectos tanto de naturaleza normativa como prospectiva. Las representaciones lógicas y simbólicas entre los elementos de un sistema de decisiones emplean recursos semánticos que describen las relaciones entre ellos de forma integral. En consecuencia, la modelación matemática como recurso de comprensión y comunicación ha merecido una creciente atención debido a la diversidad de situaciones que se presentan en un mundo dinámico y, a la vez, complejo, como el actual.

Por lo que respecta de la aplicación del AHP enfocado a la salud, Niño et al. (2020) implementaron un modelo de evaluación multicriterio en un municipio de Colombia, identificando las áreas de mayor probabilidad de transmisión del SARS-CoV-2. Por otra parte, Schmidt et al. (2015) realizaron una revisión sistemática de la literatura mediante búsquedas en las bases de datos Pubmed y Web of Science para artículos con las palabras clave en sus títulos o resúmenes: Proceso Analítico Jerárquico, Análisis de decisiones de criterios múltiples o similares, además de analizar si los autores informaron aspectos importantes y en sus estudios resultantes, afirmando que las investigaciones que aplican AHP en la salud han aumentado.

 

AHP

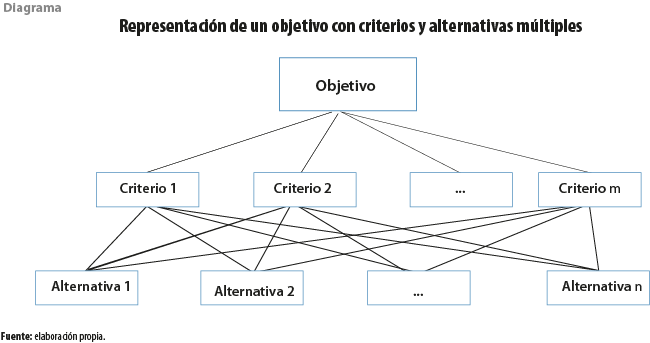
La jerarquización analítica surge a principios de la década de los 80 (T. Saaty, 1980) como un recurso metodológico que permite combinar información de carácter cualitativo, con criterios de evaluación cuantitativa. Para construir una decisión, el AHP se basa en la definición de criterios, así como en la identificación de alternativas y en la evaluación de estas con respecto a cada criterio. La teoría de procesos de jerarquización analítica, debido a su capacidad para conjuntar objetivos, criterios y diversas alternativas, es ampliamente recomendable aplicarla en la toma de decisiones bajo condiciones de incertidumbre (ver diagrama).

En el AHP, la experiencia del tomador de decisiones es esencial, ya que sus juicios subjetivos se combinan con la información cualitativa y cuantitativa disponible, dando lugar a la determinación de una priorización fundamentada y consistente para las alternativas propuestas. Así, esta información disponible referente a los criterios, ya sea cualitativa o cuantitativa, se adiciona con los juicios valorativos basados en el conocimiento y experiencia del tomador de decisiones, dando como resultado la relevancia que impacta a cada uno de los criterios establecidos en los términos relativos del conjunto.

Bajo este contexto, cabe mencionar que no existe un acuerdo unánime para elegir el mejor método a implementar en alguna situación en particular, sin embargo, está la aprobación de que esta decisión de juicio debe ser tomada por especialistas en los temas de discusión, y en conjunto con las áreas involucradas. Con respecto al grupo de expertos, existe basta literatura acerca de la importancia en la toma de decisiones, entre ellos se tiene a De Arquer (1996), Petropoulos et al. (2018) y Werner et al. (2017). Sobre el método Delphi, Linstone & Turoff (1975) y Bolger & Wright (2007) hacen notar la importancia de la experticia de los tomadores de decisiones en situaciones críticas. Un ejemplo del empleo de este método en salud pública es el realizado por el Grupo Síntevi, el cual es un consorcio dedicado a la metodología de la investigación, modelado y análisis de la evidencia científica en México. En su investigación, se describe cómo implementar el método Delphi convencional en tiempos de confinamiento, y se analizan su utilidad y limitaciones para su uso por expertos en salud para la resolución de problemas de tratamiento, diagnóstico o administrativos (Síntevi, 2020).

Cabe mencionar que la teoría del AHP ha tomado mucha atención debido al avance de la tecnología, la cual ha permitido el desarrollo de aplicaciones computacionales en los procesos operativos en el campo del álgebra matricial, llevando a cabo la simulación de escenarios, el análisis combinatorio, así como la aplicación de métodos numéricos sofisticados para el análisis de sensibilidad.

 

Metodología de aplicación del AHP

Los principios teóricos que sustentan la metodología del AHP fueron desarrollados hacia las últimas décadas del siglo XX. Fundamentalmente, se parte de las ramas de las matemáticas que tienen mayor relación con el análisis vectorial y álgebra matricial. Thomas Saaty lo creó y desarrolló en diferentes etapas (1977 y 1980), y su fundamentación matemática, en 1986, la cual se basa en estos cuatro axiomas:

Axioma 1. Referente a la condición de los juicios recíprocos. Si A es una matriz de comparaciones pareadas, se cumple que a_ij = 1/a_ij.

Axioma 2. Condición de homogeneidad de los elementos. Los que se comparan son del mismo orden de magnitud o jerarquía.

Axioma 3. Condición de estructura jerárquica o estructura dependiente. Existe dependencia jerárquica en los elementos de dos niveles consecutivos.

Axioma 4. Condición de expectativas de orden de rango. Las expectativas deben estar representadas en la estructura en términos de criterios y alternativas.

Formalmente, se tiene que si  A = {A_i} donde A_i son las alternativas, i = 1,…, n.

Una escala para el criterio c es un mapeo P_c, tal que:

P_c: A_i x A_j → a_ij

donde A_i  y A_j  son las alternativas comparadas bajo el criterio c.

Además, se tiene:

a_ij > 1 si y solo si A_i domina a A_j

a_ij = 1 si y solo si A_i es equivalente a A_j

Operacionalmente, los a_ij son obtenidos de las asignaciones de los tomadores de decisiones para los datos de la matriz A = [a_ij], donde a_ij > 0∀i,j.

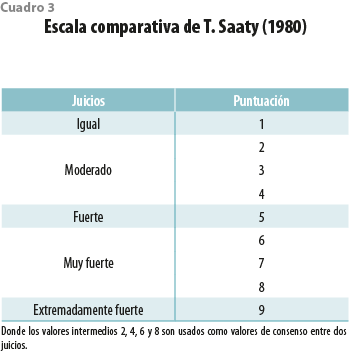
Este proceso de jerarquización evalúa (pesa) los diferentes criterios, subcriterios y alternativas en función de su importancia correspondiente en cada nivel, por lo que la técnica AHP está basada en la suposición de que el analista (decisor) puede, de manera más sencilla, elegir un valor de comparación que uno absoluto. Los juicios verbales son trasladados a una escala de puntuación (ver cuadro 3).

De acuerdo con los axiomas mencionados anteriormente, se construyen el conjunto de matrices de comparación por pares, tanto la de matriz de juicios como las matrices de alternativas, las cuales presentan la siguiente forma:

Ya obtenidas las matrices de comparación por pares, se procede a calcular las prioridades de cada criterio y/o alternativa comparada.

El proceso matemático de calcular las prioridades se llama síntesis, y en él se calculan los valores y vectores característicos de las matrices de comparación, y después se normalizan.

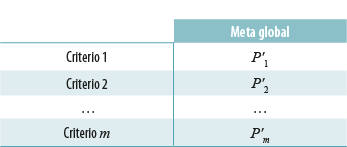
Sea P la matriz de prioridades de cada criterio (juicio) en función de la meta global:

 

donde:

m es el número de criterios.

P’_i es la prioridad del criterio i con respecto a la meta global.

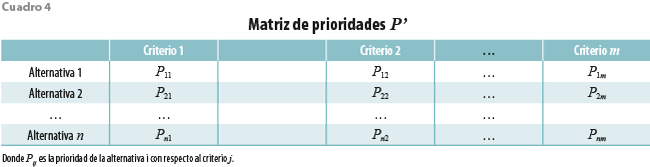
La matriz de prioridades, P’, que también expresa las prioridades de cada alternativa, en función de cada criterio, se presenta en el cuadro 4.

 

Finalmente, se tiene que la matriz de prioridad global se obtiene como el producto de P’ y P (ver cuadro 5).

Resulta una matriz (n x 1) que indica la ponderación total de cada activo en función de todas las variables explicativas, hayan sido estas cualitativas o cuantitativas.

El resultado de esta multiplicación es el vector propio asociado a la matriz de prioridades global, es decir:

donde:

El cálculo del vector propio de la matriz de comparación refleja el peso o la importancia relativa que tiene cada componente (criterio o alternativa) cuando son evaluados en su conjunto bajo cierto supuesto. Su cálculo parte de la matriz original A, donde un vector v, distinto de cero, es un vector propio de la matriz A, si para cierto escalar λ se cumple que:

Av =  λv

donde  λ  es el valor propio de la matriz A asociado al vector propio v. Con este cálculo del vector propio se obtiene la ponderación de cada una de las componentes participativas (juicios o alternativas) que son utilizadas para determinar el impacto (peso) que tiene cada una de ellas.

En cada matriz de comparación es necesario diseñar un método de priorización que permita cuantificar de forma consistente el peso de cada criterio a ser analizado (Wind & Saaty, 1980). Esta técnica AHP permite al tomador de decisiones evaluar la congruencia de los juicios con la ratio de inconsistencia (IR). Para ello, se estima el Índice de Consistencia (CI) de una matriz n x n de juicios, donde CI viene definido por:

donde  λ_max es el máximo valor propio de la matriz de criterios.

Asimismo, se calcula el I_R como:

donde RI es el valor aleatorio promedio de CI para una matriz de n x n. Los valores de RI obtenidos por R. Saaty (1987) se aprecian en el cuadro 6.

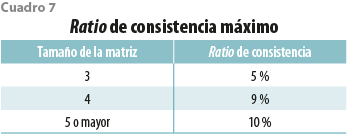
Dicho I_R deberá ser cotejado con los que aparecen a continuación, y se considerará que existe consistencia cuando no se superen los valores que se muestran en el cuadro 7.

Resultados

Para iniciar el AHP, se presenta la comparación asignada entre pares de la matriz de criterios, de acuerdo con los juicios establecidos por el GTAV acerca de los cuatro ejes de priorización para la vacunación contra el virus SARS-CoV-2 en México (ver cuadro 8).

 

El cuadro se interpreta así, por ejemplo, entre los criterios: el a (Edad de las personas) se valora dos veces más que el b (Comorbilidades personales), el a (Edad de las personas) se valora tres veces más que el c (Grupos de atención prioritaria), el a (Edad de las personas) se valora cuatro veces más que el d (Comportamiento de la epidemia), y así sucesivamente, hasta comparar todos los criterios entre pares y obtener la matriz de comparación entre pares final, cuyo vector propio correspondiente es:

donde, de acuerdo con el orden del cuadro 1, destaca la preferencia correspondiente a Edad de las personas (0.467 máximo valor de las coordenadas del vector) y la menos preferente es la referente a Comportamiento de la epidemia (0.095), lo cual es congruente con los pesos establecidos en la matriz de criterios.

Asimismo, para la construcción de las matrices correspondientes a los grupos priorizados en el orden de prelación (cuadro 2), que van a ser identificadas como las alternativas que se tienen, las cuales se comparan entre pares entre ellas dado cada criterio. Así, para el primero, en el cuadro 9 se muestra una matriz que refleja la asignación de preferencias para cada par de alternativas.

 

El cuadro se interpreta así: bajo el supuesto del criterio 1 (Edad de las personas), la alternativa 1 (Personal sanitario que enfrenta COVID-19) se valora dos veces más que la 2 (Personas adultas mayores); la 3 (Personas con comorbilidad o comorbilidades) se valora dos veces que la alternativa 4 (Personal docente de las entidades federativas), y así sucesivamente, hasta comparar todos los criterios entre pares y obtener la matriz final de comparación mostrada entre pares.

Dada esta matriz del criterio1, su vector propio correspondiente es:

Bajo el criterio 1 (Edad de las personas), y de acuerdo con el cuadro 2 de los grupos priorizados, la preferencia de las alternativas se va hacia Personal sanitario que enfrenta COVID-19 (0.419 máximo valor de las coordenadas del vector) y la última preferencia es hacia Resto de la población (mayor a 16 años de edad) (0.062 mínimo valor de las coordenadas del vector), lo cual también es congruente con lo asignado en la priorización.

De manera similar, se construyen las otras matrices bajo el supuesto de los otros criterios.

La matriz P’g de prioridades global resultante es la mejor aproximación de evaluación de los criterios analizados (T. Saaty, 1980). Este vector de prioridad es:

Nótese que el vector resultante fue igual al resultante del vector de criterios, ya que no variaron en ninguna de las matrices los pesos asignados, por lo que, de acuerdo con el cuadro 2 (grupos priorizados en la orden de prelación), su correspondencia respectiva queda ordenada igual a la establecida, esto es, la de mayor preferencia corresponde a Personal sanitario que enfrenta COVID-19, y la de menor preferencia corresponde a Resto de la población (mayor a 16 años de edad).

Es importante señalar que, con otra ponderación de los pesos asignados tanto a los criterios como a las alternativas, el orden de vacunación sería diferente.

Para validar la consistencia, a partir de λ_max que es el máximo valor propio, que resultó ser 4.031 de la matriz de criterios, se calculó el Índice de Consistencia, obteniendo un valor de CI = 0.0103, tomando a RI como 0.9, resulta ser I_R = 0.0114, el cual, cotejado con el ratio de consistencia correspondiente, implica que existe consistencia en la construcción de la matriz. Por lo tanto, se puede considerar que los criterios establecidos fueron congruentes, lo cual implica juicio racional por parte del tomador de decisiones.

Aplicación de la estrategia de vacunación

Para conocer sus resultados, se tomó la base de datos de la Secretaría de Salud (2021). De 1 048 756 registros de pacientes hospitalizados, del 1 de enero de 2020 al 31 de octubre de 2021, 412 310 dieron como resultado de laboratorio positivos a SARS-CoV-2. En la gráfica 1 se muestra el comportamiento del virus conforme a rango de edad y sexo.

 

El rango de 30 a 39 años de edad fue donde hubo la mayor concentración de casos, seguido del de 40 a 49; entre los dos captaron 44.5 % de confirmados del SARS-CoV-2.

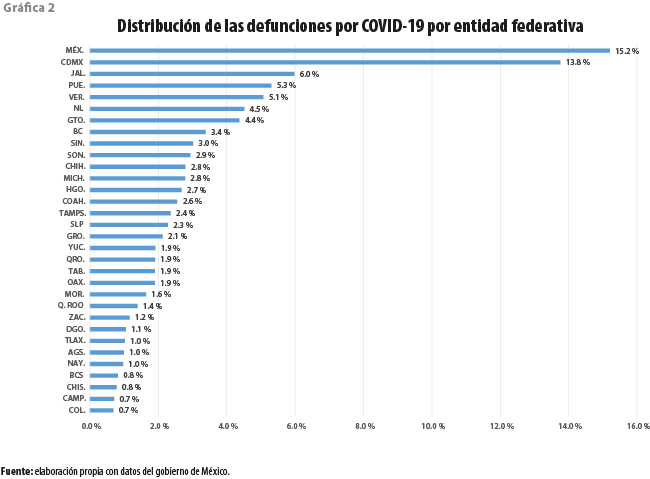
Asimismo, para conocer la distribución de las defunciones en México por entidad federativa (ver gráfica 2), se tomó la base de datos del gobierno de México con respecto al COVID-19 (2021). Los resultados obtenidos hasta el 31 de octubre de 2021 fueron que 10 estados concentraron 63.6 % de las defunciones a causa de esta enfermedad: México (15.2 %), Ciudad de México (13.8 %), Jalisco (6 %), Puebla (5.3 %), Veracruz de Ignacio de la Llave (5.1 %), Nuevo León (4.5 %), Guanajuato (4.4 %), Baja California (3.4 %), Sinaloa (3 %) y Sonora (2.9 %). El total de muertes al 31 de octubre de 2021 en México fue de 290 278.

Es importante señalar que más de 99 % de los que dieron positivo a SARS-CoV 2 presentaron síntomas de diabetes, EPOC, asma, afecciones inmunosupresoras e hipertensión, así como otras complicaciones, como cardiovascular, obesidad, renal crónica, tabaquismo.

 

Conclusiones

En la actualidad, ante situaciones complejas y apremiantes, como es este caso de la escasez de vacunas contra el COVID-19, es importante valerse de metodologías basadas en la experiencia y el conocimiento para una mejor toma de decisiones. En el trabajo desarrollado, y ante la situación de salud que se vive, bajo el supuesto de una matriz de criterios y un conjunto de matrices de prioridades de alternativas, se llegó a un vector de decisiones de alternativas.

El tratamiento de datos cuyo procesamiento, está fundamentado por la robustez matemática en su construcción, permite obtener resultados altamente satisfactorios y confiables. En este caso, la jerarquización del vector de alternativas resulta satisfactorio, ya que las alternativas por orden de prioridad son representativas de la realidad. Así, la que representa tanto a la jerarquía principal Personal sanitario que enfrenta COVID-19 como a la del último nivel de jerarquización Resto de la población (mayor a 16 años de edad) ayudan a la toma de decisiones ante la escasez de vacunas. Asimismo, se hace énfasis en la consistencia de la construcción de las matrices de comparación, que fortalece el resultado alcanzado.

Además, se debe señalar la importancia que tiene el grupo de expertos en el marco de valores para guiar en la asignación de vacunas contra el COVID-19 entre los países y a nivel nacional en la determinación de los grupos prioritarios para recibirlas, así como en la construcción de las matrices —de criterios y de alternativas—, las cuales son los insumos en este modelo de toma de decisiones, que en ambientes corporativos es un proceso complejo y extenuante, el cual, por lo general, impacta en el entorno de la viabilidad de las decisiones. Por ello, la construcción de escenarios que contemplen la combinación de objetivos, criterios y alternativas múltiples es fundamental para que los planes y programas de desarrollo estratégico tengan un fundamento sólido y ético. El resultado de la estrategia de vacunación establecida por el GTAV en la PRV exhibe la congruencia esperada en su implementación de acuerdo con nuestras necesidades apremiantes.

 

____________

Fuentes

Bolger, F., & G. Wright. “Expertise and Decision Support”, en: Springer Science & Business Media. 2007.

Centros para el Control y la Prevención de Enfermedades (CDC). COVID-19. Estados Unidos de América, 6 de abril de 2021.

Cortés, R., R. Gómez, , & X. Alba. Política nacional de vacunación contra el virus SARS-Cov-2, para la prevención de la COVID-19 en México. Documento rector. Ciudad de México, Política Nacional, Secretaría de Salud, 2021 (DE) de https://bit.ly/3VhJzA8, recuperado en el 2021.

De Arquer, M. Fiabilidad humana: métodos de cuantificación, juicio de expertos. NTP Notas Técnicas de Prevención. Madrid, España, 1996.

Gobierno de México. COVID-19 México. 22 de noviembre de 2021 (DE) https://bit.ly/3e3GFxv

Instituto Nacional de Estadística y Geografía (INEGI). Censo de Población y Vivienda 2020. México, INEGI, 2020 (DE) https://www.inegi.org.mx/

Linstone, H., & M. Turoff. “The Delphi method: Techniques and Applications”, en: Addison-Wesley Pub. Co. Advanced Book Program. Pp. 3-12, 1975.

Niño, L., O. Gutiérrez-Lesmes, C. Díaz-Celis, & F. Manrique-Abril. “Riesgo de transmisión de SARS-CoV-2: evaluación espacial multicriterio en un municipio de Colombia, 2020”, en: Rev. Salud Pública. 22(2), pp. 1-9, 2020.

OXFAM. Mega.rich recoup COVID.losses in record.time yet billions will live in poverty for at least a decade. OXFAM International, 25 de enero de 2021 (DE) https://bit.ly/3TsJSaj

Petropoulos, F., N. Kourentzes, K. Nikolopoulos, & E. Siemen. “Judgmental selection of forecasting models”, en: Journal of Operations Management. 60, pp. 34-46, 2018.

Saaty, R. “The Analytic Hierarchy Process – What it is and How it is used”, en: Mathl Modelling. 9(3), pp. 161-176, 1987.

Saaty, T. “A scaling method for priorities in a hierarchichal structure”, en: Journal Math Psych. 15(3), pp. 234–281, 1977.

_______ The Analytic Hierarchy Process, Planing, Priority Setting and Resource Allocation. New York, McGraw-Hill, 1980.

_______ “Axiomatic foundation of the analytic hierarchy process”, en: Management Science. 32(7), pp. 841–855, 1986.

Schmidt, K., I. Aumann, I. Hollander, K. Damm, & J. Graf von der Schulenburg. “Applying the Analytic Hierarchy Process in healthcare research: A systematic literature review and evaluation of reporting”, en: Medical Informatics and Decision Making. Springer Nature, 2015, doi:10.1186/s12911-015-0234-7.

Secretaría de Salud (DE) https://bit.ly/3Cf1yhO, recuperado el 31 de octubre de 2021a.

_______ (DE) https://bit.ly/3e4v69n, recuperado en octubre de 2021b.

Síntevi. “Consenso experto en tiempos de COVID-19: aplicaciones del método Delphi en materia de salud”, en: Cirugía y Cirujanos. 89(1), pp. 120-129, 2020 (DE)  https://bit.ly/3wIGQVG

Werner, C., T. Bedford, R. Cooke, A. Hanea, & O. Morales. “Expert judgement for dependence in probabilistic modelling: a systematic literature review and future research directions”, en: European Journal of Operational Reseqarch. 258(3), pp. 801-819, 2017.

WHO. WHO SAGE values framework for the allocation and prioritization of COVID-19 vaccination. World Health Organization. 14 de september de 2020 (DE) https://bit.ly/3CJFVaW

Wind, Y., T. & Saaty. “Marketing Applications of the Analytic Hierarchy Process”, en: Management Science. 26, pp. 641-658, 1980, doi: http://dx.doi.org/10.1287/mnsc.26.7.641