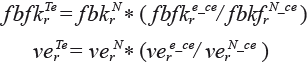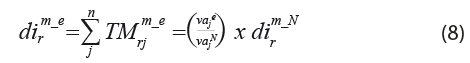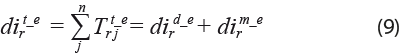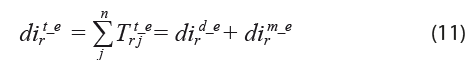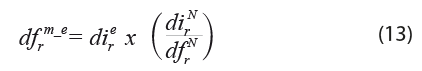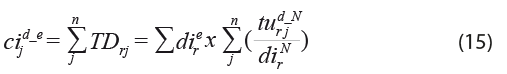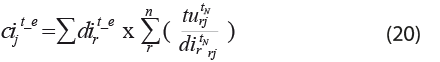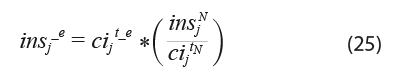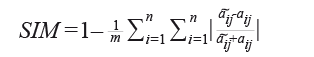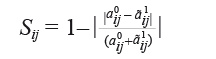Estimación de las matrices de insumo-producto por rama y sector de actividad económica de las entidades federativas de la región centro de México, 2013

 

Estimation of the Input-Output Matrices by Branch and Sector of Economic Activity of the States of the Central Region of Mexico, 2013

 

Normand Eduardo Asuad Sanén,* Esther Quiñones Luna,** José Antonio Huitrón Mendoza*** y Krista Alondra Zafra García*

* Facultad de Economía de la Universidad Nacional Autónoma de México (UNAM), nasuad@yahoo.com y economiazafra@gmail.com, respectivamente.
** Procuraduría Federal del Consumidor, equinonesl@profeco.gob.mx
*** Facultad de Economía, División de Estudios de Posgrado UNAM, jose_eco71@comunidad.unam.mx

Nota: el trabajo es parte de las actividades realizadas en el proyecto UNAM-PAPIIT con número de registro IN310319.

Vol. 14, Núm. 3 – Epub                                              Estimación de las matrices…– Epub

Los principales propósitos de este trabajo son, por un lado, mostrar la aplicación de la metodología RIISIO (Regional Integral Information System of Input-Output) para la estimación de matrices de insumo-producto regionales y estatales (MIPR y MIPE) a partir de la elaboración de cuadros de oferta y utilización (COUR y COUE), desagregadas a nivel de 262 ramas y 20 sectores de actividad económica; por otro, generar información estadística básica de insumo-producto a escala subnacional que no existe en la estadística tradicional. Cabe mencionar, que el método empleado no se encuentra para el ámbito nacional ni internacional. El resultado de esta investigación dio lugar a la construcción de 36 COUE, un COUR, 34 MIPE y dos MIPR por rama y sector para el 2013 de las entidades federativas que integran la región centro (Ciudad de México, México, Hidalgo, Morelos, Puebla y Tlaxcala) y una tabla de COU y MIP agregadas del resto del país. Por último, cabe destacar que los datos estimados son consistentes con las cuentas nacionales y el error de eficiencia de la estimación arroja errores mínimos. Palabras clave: cuadros de oferta y utilización estatales; matrices de insumo-producto estatal y regional; metodología RIISIO.

The main purposes of this work are, on the one hand, to show the application of the RIISIO (Regional Integral Information System of Input-Output) methodology for the estimation of regional and state input-output matrices (MIPR and MIPE) from the elaboration of supply and use tables (COUR and COUE), disaggregated at the level of 262 branches and 20 sectors of economic activity; on the other hand, to generate basic statistical information of input-output at subnational scale that does not exist in traditional statistics. It is worth mentioning that the method used is not available at the national or international level. The result of this research led to the construction of 36 COUE, one COUR, 34 MIPE and two MIPR by branch and sector for 2013 for the states that make up the central region (Mexico City, Mexico, Hidalgo, Morelos, Puebla and Tlaxcala) and a table of COU and MIP added from the rest of the country. Finally, it should be noted that the estimated data are consistent with the national accounts and the estimation efficiency error yields minimal errors.                                                                           Key words: state supply and use tables; state input-output matrices; bottom-up methodology RIISIO.

Recibido: 30 de septiembre 2022
Aceptado: 07 de febrero 2023

 

1. Antecedentes

Las matrices de insumo-producto (MIP) son una herramienta que permite analizar de forma integral la estructura y el funcionamiento de la economía de un país, región, estado, municipio, zona y área. Este análisis, tradicionalmente, se realiza a partir del comportamiento de la producción al variar la demanda final (DF) y sus componentes: consumo privado, gasto de gobierno, inversión, exportaciones e importaciones. Esto hace posible evaluar los impactos económicos que se generan en la producción, el valor agregado (VA) y el destino del gasto. Ello ha sido elemental para los planteamientos de política económica que son sustento para la toma de decisiones gubernamentales y de las empresas. Su construcción a nivel nacional se realiza mediante la elaboración de las cuentas nacionales, en particular de los cuadros de oferta y utilización nacionales (COU_N) y a partir de estos se elabora la matriz nacional (MIP_N).

A nivel subnacional que corresponde al interior del país integrada por regiones económicas, la construcción de las matrices regionales (MIP_R) no sigue la metodología internacionalmente aceptada que se utiliza para el desarrollo de las nacionales. La principal razón que se argumenta en la literatura es la insuficiencia de datos estadísticos, lo que significa la no elaboración de las cuentas económicas regionales para que a partir de ellas se construyan las matrices de insumo-producto regionales como recomiendan los lineamientos de la ONU para la matriz nacional. Este problema ha sido planteado desde los trabajos pioneros de Leontief y Strout (1963), Miller y Blair (2022), Hewings (2020) y Martins et al. (2017), así como en el propio manual de EUROSTAT (2008). De hecho, en el ámbito mundial se carece de normatividad metodológica para la construcción de las tablas y matrices a escalas subnacional y regional, lo que ha reforzado la utilización de métodos indirectos, principalmente a través de coeficientes.

En consecuencia, en México y en general a nivel internacional, la construcción de MIP_R se ha llevado a cabo mediante el método de coeficientes regionales para distribuir los datos de la MIP_N por regiones o áreas subnacionales de los países. En la literatura se le denomina regionalización de la matriz nacional y, para ello, se emplea una serie de coeficientes de participación representativos de la economía de las entidades federativas o áreas geográficas bajo estudio. A este procedimiento se le conoce como método de arriba hacia abajo para la construcción de las MIP_R y las estatales (MIP_E), las cuales se elaboran a partir de la nacional, bajo el supuesto de que las regiones con respecto al país solo varían en escala y composición productiva.

Una exposición detallada del cálculo de los coeficientes de localización se encuentra en Miller y Blair (2022, pp. 441-457). De estos métodos destaca la propuesta de Flegg et al. (1995), la cual consistió en incorporar a los coeficientes cruzados de compradores y vendedores regionales con respecto al país el tamaño económico de la región, representado por la letra λ, lo que se especificó como el coeficiente de localización de Flegg: . En su estimación se utiliza como variable el empleo para calcular el tamaño relativo de la región, no obstante, surge el problema de especificar el valor de δ para obtener λ y no es claro cuál debe ser este, donde: , donde 0 < δ < 1.

El trabajo empírico sobre algunos casos de estudio ha arrojado para δ un valor de 0.3, no obstante, varias investigaciones posteriores han señalado que el apropiado de δ varía considerablemente entre regiones, por lo que es inadecuado fijarlo con anticipación en ese valor. Esto llevó a Flegg y asociados a modificar el Índice de Localización como respuesta a las críticas de su concepción y uso, propuestas que se presentan en Flegg y Weber (2000), Flegg y Tohmo (2013) y Kowalesnski (2015). En síntesis, modificaron el índice original eliminando el valor de δ e incorporaron el coeficiente de localización para crear el Índice Aumentado de Localización:  A partir de este se estiman los coeficientes tecnológicos regionales, de tal forma que si el de localización es mayor a 1,  se multiplica por los técnicos nacionales, , y, en caso de que sea menor, , entonces  se multiplica por . Sin embargo, como lo señalan Miller y Blair (2022, p. 452), la evidencia de estudios empíricos de la aplicación del nuevo coeficiente de Flegg no aporta ningún cambio considerable. Por último, cabe referir los trabajos de Pereira-López et al. (2020 y 2021), que muestran que los coeficientes de localización de Flegg y asociados no son adecuados para la construcción de matrices regionales, por lo que desarrollan otro método que denominan una metodología de coeficientes de localización de dos dimensiones 2D-LQ; sus cálculos muestran tener un mayor nivel de precisión en las estimaciones de MIP_R o modelos multiregionales en comparación con los que solo emplean coeficientes de localización basados en el método de Flegg. De ahí que podamos concluir que los coeficientes de localización aún están en debate, ya que su aplicación para la construcción de las MIP_R se considera ineficaz y sin soporte teórico.

No obstante, el problema más importante del uso de los coeficientes de localización no es su eficiencia, ya que en su aplicación no toman en cuenta la construcción de las cuentas regionales y su integración en los cuadros de oferta y utilización para la estimación de las matrices de insumo-producto, como lo señala la metodología internacional, por lo que su empleo para la elaboración de las MIP_R de hecho no considera las particularidades y tipo de transacciones económicas de las regiones, asumiendo que son semejantes a las nacionales, solo diferenciadas por el tamaño y la composición productiva, lo que implica igual tecnología y organización productiva.

De hecho, con la finalidad de comparar los resultados de la construcción de una matriz regional, la del estado de Sonora, mediante el método de coeficientes a través de la metodología de arriba hacia abajo con respecto a la de abajo hacia arriba, se llevaron a cabo dos investigaciones: Asuad, N y Sánchez, J. (2016 y 2018), cuyos resultados mostraron que la MIP construida de arriba hacia abajo es una versión reducida a escala de la nacional, ya que omitió sectores de actividad económica de la entidad cuya existencia se podría fácilmente constatar con datos censales y presentó encadenamientos entre sectores económicos que no corresponden a los que en realidad se llevan a cabo a nivel subregional en ese estado.

Por el otro lado, la MIP de Sonora construida de abajo hacia arriba mediante la elaboración de matrices subregionales recoge de manera más fidedigna la actividad económica de la entidad al considerar las diferencias subregionales que se llevan a cabo. Bajo esta concepción se realizó la investigación que se encuentra descrita en Asuad (2020): Modelo UNAM para construir desde abajo matrices de insumo-producto regionales por entidad federativa para México 2008.

La metodología que se elaboró permitió la construcción de los COU_E y las matrices de insumo-producto para las 32 entidades federativas del país considerando un modelo unirregional abierto al exterior y cerrado al interior del país, semejante al que se construye a nivel nacional. La desagregación de los datos fue a escala sectorial, lo que implicó considerar los 20 sectores de actividad económica considerados por el Instituto Nacional de Estadística y Geografía (INEGI). Para ello, se utilizó la metodología RIISIO (Regional Integral Information System of Input-Output) que en esencia consiste en la elaboración del Sistema de Información Integral Regional de Insumo-Producto basado en la construcción de cuentas económicas estatales. Su concepción teórica corresponde a un enfoque económico espacial, por lo que a partir de este se elaboraron los COU_R y las MIP_R de abajo hacia arriba.

No obstante, el método elaborado es híbrido ya que los datos existentes de regiones y estados son insuficientes y se completan con información nacional. De ahí que la orientación metodológica se dirigiera a crear el sistema de información para la construcción de las cuentas regionales de manera semejante a la nacional. Los datos a niveles estatal y municipal se encuentran fragmentados en varios sistemas; además, las estadísticas oficiales a escala subnacional que se presentan en los censos Económicos y de Población y Vivienda del INEGI, y en los anuarios estadísticos por entidad federativa, son parciales y no coinciden al totalizarse con las cuentas nacionales de producción, ingreso y gasto.

La información económica censal es parcial, pues recoge fundamentalmente los datos económicos del sector privado y solo una parte de los gubernamentales; por esta razón no coincide con los totales de las cuentas económicas a escala nacional. Su diferencia es significativa ya que si se considera el valor agregado censal bruto total corresponde solo con 39 % del Producto Interno Bruto total del país, lo que, sin duda, dificulta aún más la elaboración de los COU y MIP a niveles regional y estatal.

De ahí la necesidad de crear un sistema de datos estadísticos integral con una perspectiva espacial de insumo-producto que tenga su origen, por un lado, en las unidades espaciales bajo estudio y, por otro, en la generación de información acorde con los requerimientos de las identidades contables (IC) de esos espacios para la construcción de los COU_E y las MIP_E.

A pesar de los avances de la metodología mencionados, el nivel de agregación analizado se ha hecho solo a 20 sectores de actividad económica, de ahí que el principal propósito de esta investigación sea la de aplicar la metodología RIISIO desagregando el análisis a 262 ramas de actividad económica y 20 sectores mediante la elaboración de los cuadros de oferta y utilización estatales que integran la región centro del país para la construcción de la matriz de insumo-producto de cada una de las entidades federativas y de esa región económica de México para el 2013. Además, se pretende poner a disposición de los interesados en el análisis insumo-producto información estadística básica que permita una comprensión más detallada del sistema económico estatal y regional con sus interdependencias y comportamiento en su conjunto.

El estudio comprende las siguientes entidades: Ciudad de México, Estado de México, Hidalgo, Morelos, Puebla y Tlaxcala; además, se construyen COU y MIP agregados de la región centro y del resto del país. Asimismo, se verificó la consistencia estadística de la estimación de los COU regional y estatal al totalizarlos y compararlos con los resultados de los COU_N para el 2013, que elaboró el INEGI, esto mediante la utilización de los índices tradicionalmente empleados en la literatura de insumo-producto para evaluar el error de estimación: Índice Desviación Media Porcentual e índices de Similitud de Isard-Romanoff y de Leontief Modificado.

En las siguientes secciones se presentan la metodología y sus etapas, precisando los detalles de cada una de estas con el fin de que se tenga una comprensión detallada de la elaboración tanto de las cuentas estatales como de los cuadros de oferta y utilización, y de las matrices de insumo-producto estatales y regional. El estudio se integra con el siguiente contenido: 1. Antecedentes, 2. Estimación de los COU y MIP estatales y región centro, 3. Resultados empíricos y 4. Conclusiones y reflexiones finales.

 

2. Estimación de los COU y las MIP estatales y región centro

La metodología RIISIO se aplica para su estimación y se sustenta en la concepción del modelo uniregional abierto al resto del mundo cerrado al interior del país, es decir, considerando el comercio exterior, de la misma manera en que está construida el MIP_N, sin considerar el comercio subnacional. Por esa razón, los datos de insumo-producto se estiman a precios básicos del 2013, ya que a los de comprador implicaría conocer el comercio intrarregional de la región centro que llevan a cabo los estados que la integran, y el que realiza esta con el resto del país. Además, se elabora una tabla y matriz de insumo-producto correspondiente al resto del país, que se calcula como la diferencia entre la MIP_R y la nacional agregada para el 2013. Las etapas establecidas para la elaboración de este trabajo se muestran en el cuadro 1.

 

 

Etapa 1. Análisis de la estructura productiva y funcionamiento de la región centro 2008-2013²

Para ello, se aplicó la metodología del subsistema de Información de Unidades Económico-Funcionales (FERIS), que forma parte de la metodología RIISIO. En síntesis, primero se identificó y delimitó la región centro mediante el análisis comparado de la concentración económico espacial y los flujos de interacción, valor agregado, empleo, producción bruta total, por entidad y sector. Posteriormente, se comparó la composición de la estructura productiva por sector de actividad económica a nivel rama para ambos años, para lo cual se tomaron los datos de los Censos Económicos por entidad federativa del valor agregado de las 262 ramas de cada año.

Etapa 2. Estimación de las variables clave de la DF y VA por entidad y región centro a nivel rama del 2013

Esta se inicia con la evaluación y procesamiento de datos espaciales, bajo los lineamientos del FERIS del método RIISIO, que en esencia consiste en calcular estas variables y posteriormente, a partir de ellas, elaborar las identidades contables para la construcción de las cuentas estatales y de la región centro. Cabe aclarar que el VA y la DF, por ser componentes fundamentales de las IC, se consideran como anclas, ya que sus valores integran el resto de las variables que forman las identidades. Además, otra distinción importante de su compilación y estimación es que su cálculo se realizó a partir de diversas fuentes de información estatales y de datos nacionales y, después, se hicieron consistentes con estos.

La estimación de estas variables es híbrida, ya que se realizó a partir de datos estatales, complementados con nacionales, sin embargo, su cálculo parte de información estatal, lo que la caracteriza como una estimación de abajo hacia arriba, es decir, de la región al país, a diferencia del enfoque tradicional de arriba hacia abajo, denominada en la literatura de insumo-producto como regionalización de los datos nacionales, que de manera breve consiste en la distribución regional de los valores nacionales. Para ello, se utiliza una variable representativa regional a nivel nacional, como puede ser el caso la aportación del empleo regional en el país, por lo cual se aplica el método de coeficientes de participación del empleo asumiendo por ejemplo que es representativo de la contribución del valor agregado bruto regional (VAB_R), por lo que se multiplica dicho porcentaje por el VAB nacional para obtener el regional (Miller y Blair, 2022, p. 67).

2.1. Estimación del VAB_E

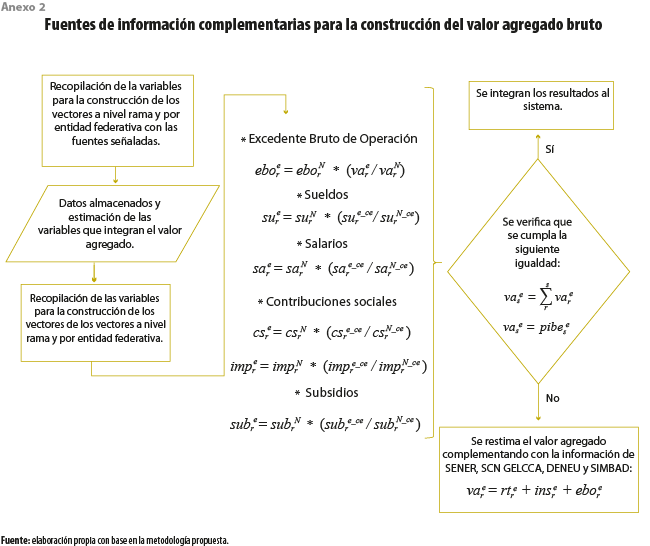
La variable de valor agregado bruto estatal (VAB_E) no se puede tomar directamente de los Censos Económicos debido a que este indicador representa en promedio 38.3 % del total del Producto Interno Bruto Estatal (PIBE) reportado por el INEGI, por lo que fue necesario considerar diferentes fuentes de información a este nivel de análisis. Los datos del VAB_E fueron estimados a partir de diversas fuentes: Censos Económicos, Sistema Estatal y Municipal de Bases de Datos y Sistema de Cuentas Nacionales de México (SCNM), del INEGI; Secretaría de Energía (SENER); y portal del Servicio de Información Agropecuaria y Pesquera (SIAP) de la Secretaría de Agricultura y Desarrollo Rural (SADER).³ Esta estimación se realizó por entidad federativa de la región centro, compilando los datos de la Ciudad de México, el estado de México, Morelos, Hidalgo, Puebla, Tlaxcala y el resto del país para el 2013, a un nivel de desagregación de actividad económica de 262 ramas y 20 sectores a precios básicos y constantes del 2013.

El valor agregado se estimó a partir de la suma del pago a factores productivos mediante la siguiente identidad contable⁴:

donde e corresponde a entidad y r, a rama. De ahí que  sea el valor agregado; , las remuneraciones totales; , los impuestos netos de subsidios; y , el excedente bruto de operación.

Los vectores de remuneraciones totales  y los impuestos netos de subsidios  son construidos a partir de las siguientes identidades contables:

   

donde  son los salarios; , los sueldos; y , las contribuciones sociales; por su parte,, los impuestos y , los subsidios.

El procedimiento de cálculo de cada una de las variables que conforman el valor agregado estatal a nivel rama para las entidades federativas de la región centro de México se realizó, primero, de manera preliminar y, posteriormente, definitiva.

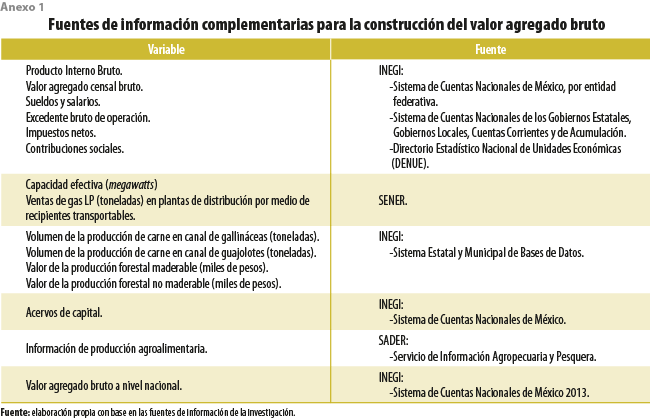
La estimación preliminar del VAB_E y de sus componentes se hizo mediante la regionalización indirecta, es decir, a partir de cada variable estimada estatalmente, la cual se multiplicó por la variable nacional correspondiente, con excepción del excedente de explotación estatal, debido a que no se cuenta con ese dato en las entidades federativas. Además, la mayor parte del valor agregado corresponde a dicho rubro, por lo que se tuvo que estimar a partir de multiplicar la participación porcentual del VAB_E en el nacional multiplicado por el excedente de explotación nacional (ver Anexo 2). Después, se realizó el cálculo definitivo del valor agregado estatal; para ello, primero se compararon las diferencias de la estimación preliminar del VAB_E con la que se obtiene de la participación porcentual del PIBE a nivel rama debido a que contablemente deben ser iguales. Por ello, a partir de la diferencia del VAB_E estimado con la regionalización indirecta con respecto al VAB_E a partir del PIBE, se reestimaron los valores por rama que diferían, manteniendo la participación estatal de cada rama de acuerdo con el PIBE, pero con un nuevo valor absoluto de sus componentes (ver Anexo 2).

Además, se estableció como condición que las remuneraciones totales, impuestos netos de subsidios y excedente bruto de operación debían encontrarse dentro de los límites estimados del valor agregado con el fin de que exista congruencia entre la información de ramas de actividad de las entidades de cada componente y el total de valor agregado en términos de estructura económica y disponibilidad de la información de cada componente con el valor agregado total registrado. Finalmente, los valores obtenidos del VAB_E y de sus componentes se incorporaron en el sistema de tablas de oferta y utilización.

2.2 Estimación de la DF y sus componentes

Esta se realiza a partir del cómputo del total del consumo privado, el gasto de gobierno, la inversión, la variación de existencias y las exportaciones netas del COU_R de la economía total, como se expresa en la siguiente identidad:

donde  la demanda final total; , el consumo privado total; , el consumo de gobierno total; , la formación bruta de capital fijo total; , la variación de existencias total; y las exportaciones totales.

Para la obtención del vector de consumo privado a niveles rama y entidad federativa, se consideró como fuente la Encuesta Nacional de Ingresos y Gastos de los Hogares (ENIGH)⁵. Cabe señalar que sus datos no son compatibles con el Sistema de Clasificación Industrial de América del Norte (SCIAN), por lo que en esta parte del proceso de compilación de los datos se utilizó una equivalencia de acuerdo con cada uno de los productos, como se muestra a manera de ejemplo en el cuadro 2 para la rama de actividad de cultivo de otras hortalizas.

 

 

Después, se procedió a agrupar la información por estado. Sin embargo, dado que la suma del total de consumo privado de las entidades federativas por rama obtenido con la ENIGH no coincide con el total del vector de consumo privado nacional reportado en las tablas de oferta y utilización, se regionalizaron también de manera indirecta los datos para obtener el total nacional, de acuerdo con la siguiente expresión:

donde  es el consumo privado total; , el consumo total nacional de los cuadros de oferta y utilización; , el consumo privado por estado y rama de la ENIGH; y , el nacional por rama de la ENIGH.

En el caso del vector de consumo de gobierno, se tomó la información de gasto total por entidad federativa del SIMBAD y se regionalizó a rama, asumiendo la misma proporción sectorial a nivel nacional, por lo que el valor absoluto del consumo de gobierno estatal de cada rama dependerá del monto de gasto total registrado por cada entidad, en términos de la siguiente relación:

 

 

donde  es el consumo de gobierno por entidad y nivel rama; , el total por estado del SIMBAD; , el nacional a nivel rama; y , el total nacional.

Finalmente, para asegurar la coincidencia de los cálculos con el total de gasto de gobierno nacional registrado en las tablas de oferta y utilización, se realiza una regionalización de los datos por entidad federativa respecto al total nacional, como se muestra a continuación:

 

donde es el consumo de gobierno total por entidad (e) y rama (r); , el total por entidad del SIMBAD; , el nacional y nivel rama; y , el total nacional de los COU.

El cálculo para los vectores de la formación bruta de capital fijo y variación de existencias se efectúa con información de los Censos Económicos, por lo que debe considerarse que en esta parte del procedimiento los datos solo permiten aproximar la estructura económica de cada entidad, es decir, únicamente la participación de cada uno de los sectores en las entidades y no su valor, ya que si se comparan los totales correspondientes al censo con los reportados en el SCNM, la información representa solo 15.17 por ciento.

Las diferencias metodológicas y el tamaño de la muestra son las principales causas de la brecha en las estimaciones, sin embargo, los Censos Económicos proporcionan datos relevantes sobre el comportamiento económico de una entidad federativa o un municipio, en sus distintos niveles de desagregación de actividad económica (sector, subsector, rama, subrama o clase). Con la información obtenida, estos componentes se expresan mediante la regionalización indirecta para ser consistentes con los datos nacionales de la siguiente forma:

 

donde  es la formación bruta de capital fijo total por estado y a nivel rama; , la del país; , la formación bruta de capital fijo por estado y rama de Censos Económicos; , la nacional a nivel rama de Censos; , la variación de existencias por entidad federativa a nivel rama; , la variación por estado y rama de Censos; , la nacional a rama de Censos; y , la variación nacional a nivel rama de los COU.

En el caso de las exportaciones e importaciones a rama, como solo se cuenta con información a nivel sector y subsector del periodo del 2007 al tercer trimestre del 2019, fue necesario estimarlas, para lo cual se recurrió a los datos del Atlas de complejidad económica de la Secretaría de Economía.

Esta información es posible obtenerla a nivel estatal, no obstante, su sistema de clasificación corresponde al de la Tarifa de la Ley de los Impuestos Generales de Importación y de Exportación (TIGIE), por lo que se reclasificaron los sectores con el fin de hacerlos comparables con el SCIAN, procedimiento que a manera de ejemplo se muestra en el cuadro 3.

 

 

A continuación, se ordenaron las ramas por entidad federativa, y para hacerlas consistentes estadísticamente con los COU_N se regionalizaron de manera indirecta; para ello, las exportaciones por entidad federativa se estimaron considerando su participación por rama a nivel nacional multiplicada por las nacionales por rama de la siguiente forma:

 

donde  son las exportaciones por entidad y rama; , las nacionales por rama de los COU; , las exportaciones por entidad y rama del Atlas de complejidad económica; , las exportaciones nacionales a nivel rama del Atlas. En el caso de las importaciones, si bien se cuenta con una primera estimación, esta es una de las variables que se modifican con la recalibración del Sistema de Cuentas Regionales que se explica posteriormente; de manera adicional, el valor de las exportaciones se valida con los datos reportados por el INEGI para los sectores de la industria manufacturera y de la minería.

Etapa 3. Estimación del Sistema de Cuentas Regionales y su calibración

La estimación del Sistema de Cuentas Económicas Estatales se inicia con los datos calculados del VA y la DF, a partir de los cuales se obtienen las identidades contables de los COU_E, por lo que una vez que se tienen los vectores de las IC estatales, se procedió a validar el equilibrio entre la oferta y la utilización por estado a través de su calibración y balanceo. Las cuentas económicas estatales se validan al cumplir con el equilibrio contable entre sí y el de las IC a nivel estatal con el total de las entidades federativas, que reflejan el agregado nacional.

El análisis se inicia a partir de las identidades contables de la oferta y demanda totales, consideradas en equilibrio, para lo cual se estiman los COU_E diferenciando las que corresponden a la economía total, doméstica e importada de las entidades federativas de la región centro. Se utilizan los vectores del valor agregado y la demanda final obtenidos anteriormente; para ello, se empieza con las IC de oferta y utilización en equilibrio, después se calcula la demanda intermedia a niveles doméstico, importado y total mediante la regionalización indirecta usando los coeficientes de mercado a partir de las ventas, es decir, por renglón o fila y se continúa a partir de considerar el equilibrio entre el consumo intermedio y la demanda al aplicar el mismo modelo que corresponde a los coeficientes de mercado, pero desde la perspectiva de las compras, esto es, por columna.

La oferta total estatal por rama es igual a la utilización total estatal , que se integra por la oferta doméstica estatal por rama  más las importaciones , lo que se especifica como:

 

La  por rama es igual a la suma de la demanda intermedia total estatal por estado por rama  más la demanda final total estatal por rama , lo que se denota como:

Contablemente, las identidades de la oferta y utilización totales se consideran en equilibrio, que se expresa como:

La demanda intermedia doméstica estatal por rama  se obtiene mediante la estimación de los coeficientes de mercado , lo que es igual a la participación del valor agregado estatal por rama  entre el valor agregado nacional de esa rama , proporción que se multiplica por la demanda intermedia doméstica nacional  y se formaliza de la siguiente manera:

La demanda final doméstica estatal por rama es función de la demanda final total estatal menos las importaciones totales  lo que a su vez es igual a la oferta doméstica, que se especifica como:

 

 

De ahí que la demanda intermedia de las importaciones   se obtenga a partir de los coeficientes de mercado de importación por estado y rama , lo que se lleva a cabo utilizando la participación del valor agregado estatal por rama   en el nacional  y al multiplicarse dicha proporción por la demanda intermedia nacional por rama , lo cual se expresa como:

En el caso de las importaciones de la demanda final , esta simplemente se obtiene por diferencia al restar de las importaciones estatales por rama  las intermedias por estado y rama , lo que se expresa como:

por lo que las importaciones de la demanda final estatal por rama  se integran por las intermedias del estado por rama menos las finales  , expresada como:

 

En el caso de la demanda intermedia total estatal por rama , se estima mediante los coeficientes de mercado totales estatales por rama , que son resultado de la suma de la demanda intermedia doméstica estatal por rama   más la intermedia de importaciones estatal por rama . La identidad se especifica como:

La demanda final total estatal por rama  es la suma de la doméstica  y la de importaciones estatales por rama ; a su vez, esa demanda se calcula al multiplicar la intermedia estatal por rama   por la participación de la intermedia nacional por rama  en el total de la final nacional de las ramas, lo que se denota como:

 

Para construir los cuadros de oferta, el modelo utilizado para su elaboración es similar al empleado para el caso del cuadro de utilización a través de los coeficientes de mercado. No obstante, su análisis se realizó desde la perspectiva de las compras, esto es, con base en los datos del valor agregado y la utilización. Su estimación parte de la igualdad del total de las variables del consumo intermedio doméstico estatal por rama  y el de la demanda intermedia estatal por rama , expresada como:

de tal forma que el consumo intermedio doméstico estatal por rama se calcula a partir de los coeficientes de mercado doméstico de las entidades federativas por rama obtenidos a partir de las compras, es decir, al multiplicar la demanda intermedia estatal por rama, multiplicada por la sumatoria de las compras domésticas a nivel nacional por rama   dividido entre el total de la demanda intermedia a escala nacional por rama ( ), especificado como sigue:

El equilibrio de las variables entre el consumo intermedio  y la demanda intermedia de las importaciones  se mantiene de la misma manera que en la expresión anterior, lo que se expresa como:

 

donde el consumo intermedio estatal de las importaciones por rama se integra por la diferencia del consumo intermedio total por estado y rama   y el doméstico estatal por rama  expresado como:

La estimación del equilibrio del consumo intermedio y la demanda intermedia total estatal por rama sigue la misma lógica que el consumo intermedio doméstico y el de importación, expresados como:

 

Así, el consumo intermedio estatal total por rama se integra por la suma del doméstico por estado y rama  y el doméstico importado estatal por rama  , expresado como:

 

Por último, dado el equilibrio e igualdad entre el total del producto bruto total por estado y rama  y el total de la oferta doméstica  y que el producto bruto total por entidad es igual al consumo intermedio total más los impuestos netos de subsidios y sumando también el valor agregado, cada uno por estado y rama, se procede a estimar los componentes del producto bruto total a partir de las siguientes expresiones:

 

sustituyendo el valor de   a partir de la siguiente expresión:

En el caso de los impuestos y el valor agregado, se estiman como:

 

A continuación, se valida el equilibrio de las cuentas estatales y en caso de desequilibrios se requiere aplicar un proceso de calibración⁶ a partir de la demanda intermedia doméstica considerando que, si el desequilibrio corresponde a la oferta o la utilización, la diferencia o incremento se ajusta reduciendo o aumentando la demanda intermedia doméstica, procediendo a su equilibrio según sea el caso, como se muestra a continuación:

 

 
El ajuste de la nueva demanda intermedia se integra como vector en los sistemas de cuentas estatales y regionales, lo que implica el reestimar el valor de la demanda final doméstica, observando que los valores no sean negativos y asegurar que la oferta doméstica sea igual a la utilización doméstica y la total:

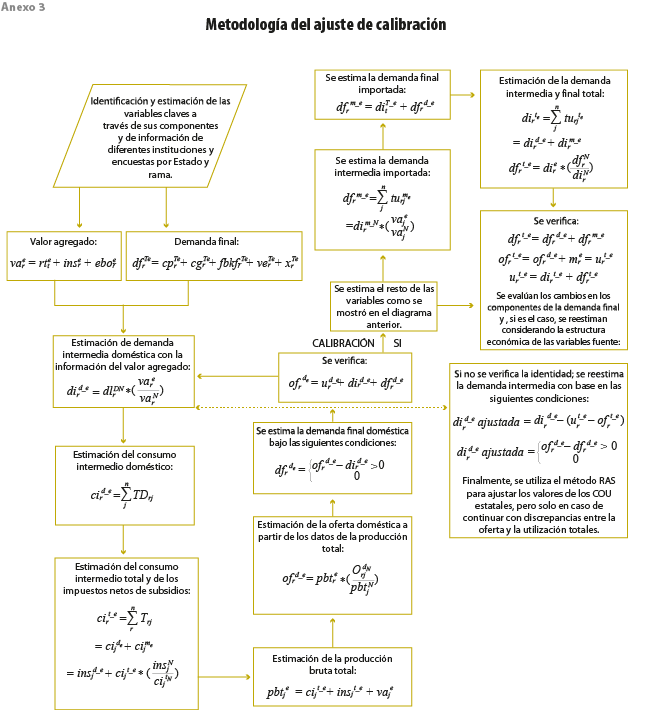
La corrección se realiza cuando el error es mínimo y el sistema se encuentre completamente en equilibrio en todas sus identidades contables. Además del equilibrio de las cuentas estatales y regionales, al totalizarse los montos estos deben ser consistentes con los valores nacionales, ya que no deben arrojar cifras negativas, lo cual implicaría que los valores del vector estimado de las entidades federativas y la región centro están por arriba de lo reportado a nivel nacional. Los desequilibrios existentes de acuerdo con la metodología empleada provienen de una subestimación o sobrestimación de la demanda intermedia doméstica. Asimismo, se observó que el valor de los impuestos netos de subsidios fuera proporcional al ajuste realizado (para ver una síntesis de la metodología de calibración, se recomienda consultar el diagrama del Anexo 3).

Etapa 4. Transformación de las tablas de oferta y utilización en matrices simétricas de insumo-producto

Esta se inicia con la transformación de los COU_E en MIP_E a partir de la metodología sobre los modelos de EUROSTAT (2008). Además, para su construcción, se consideran los utilizados por el INEGI a nivel país, que corresponden a los modelos B y D, respectivamente, producto por producto e industria por industria; también se obtienen las matrices de coeficientes directos e indirectos.

El modelo de industria por industria asume ventas fijas de productos en los que cada uno tiene su propia estructura de ventas específica, independiente de la producción de la industria. Por otra parte, el de producto por producto supone que cada industria tiene su propia forma de producción específica, independiente de la combinación de bienes o servicios que produzca. Estos modelos permiten estimar la demanda intermedia, el valor agregado, la demanda final y la producción en formatos de producto por producto e industria por industria tanto en la economía total como en la doméstica y en la importada.

La transformación de los COU_R a MIP_R totales, domésticas e importadas se realizó con base en el modelo D sugerido por EUROSTAT (2008, pp. 347-357) que se describe como de industria por industria bajo el supuesto de que la estructura de ventas es fija y que cada producto tiene una específica, independientemente de la industria en la cual se produce. Los componentes necesarios para el modelo se consignan en el cuadro 4.

 

Etapa 5. Agregación a nivel sectorial de las MIP a escala rama para el 2013

Esta consiste en totalizar las relaciones a nivel rama (cuatro dígitos del SCIAN) para obtener al de sector los componentes de las matrices (dos dígitos SCIAN), de tal manera que, por ejemplo, para obtener cada uno de los elementos de la matriz de transacciones Z_ij a escala sector, se suman las transacciones entre las ramas que componen un sector i consigo mismo y de la misma forma se realiza el procedimiento para agregar las relaciones con respecto a los sectores j. Cabe mencionar que estas matrices coinciden con las que publica el INEGI.

Este procedimiento se llevó a cabo empleando un método informático con el paquete ioanalysis de R (Wade y Sarmiento-Barbieri, 2020, p. 4); la forma en la que está planteada la agregación se explica de manera detallada en Miller y Blair (2022, pp. 161-165).

Hasta este punto se ha presentado la manera en la que se recopilaron y estimaron los datos estadísticos para la construcción de los COU_R, identificando cuáles eran las necesidades de información adicional para las entidades de la región centro a nivel de rama. De la misma forma, se ha precisado cómo se construyó lo que denominamos el Sistema de Cuentas Regionales, el cual es un elemento necesario para conciliar estadísticamente la información, esto en dos sentidos: 1) que las cuentas de cada uno de los estados estén en equilibrio y 2) que los resultados sean consistentes con los COU_N. Por último, se estimaron las matrices de insumo-producto. Los resultados se comentan en el siguiente apartado.

Etapa 6. Análisis de eficiencia de la estimación de los COU_E⁷

Cuando se estiman o construyen MIP_R mediante métodos híbridos, no es común realizar un análisis de eficiencia sobre su construcción debido a la falta de una matriz de referencia para su comparación. En el caso de una MIP, actualizada o proyectada a partir de otra, existe una serie de índices que miden la eficiencia de su estimación y, en consecuencia, la magnitud del error en los datos, esto es, la diferencia que hay entre esta y la matriz de origen (Miller y Blair, 2022).

En estas investigaciones, usualmente se calcula una serie de índices que miden el error que puede haber en las estimaciones, como el Índice de Theil, la distribución de la chi-cuadrada, el Índice de Cambio Relativo, error porcentual total, diferencia de medias relativas, prueba no paramétrica de Wilcoxon, coeficiente de correlación y el análisis de regresión (Hewings, 1984).

En este trabajo se emplean las medidas tradicionales de eficiencia de la estimación al calcular el error cuando se comparan las matrices estimadas con las de referencia. La forma en la que se interpretan estos índices difiere debido al supuesto de la tecnología estatal, que se asume es diferente de la nacional. Los generalmente utilizados son el de MAPE propuesto por Butterfield y Mules (1980), el SIMISARD de Langford y Romanoff (1968) y, por último, el SIMIL⁸. Además, se usa el Índice de Desviación Media Absoluta (MAD), no obstante, Lahr (1993) señala que no permite identificar los errores que pueden provenir de los valores extremos, por coeficientes muy altos o bajos; asimismo, menciona que la magnitud de la medida cambia con el número de sectores de las tablas de insumo-producto que se evalúan.

La interpretación de estos índices es semejante, ya que de manera simple corresponden a medidas de distancia entre los valores de la matriz estimada con respecto a la de referencia o matriz base. En el caso del MAPE, las discrepancias mínimas corresponden a valores cercanos a 0, mientras que en los índices de Similitud de Isard-Romanoff y Leontief Modificado, el 0 representa la máxima diferencia en tanto que el 1, la mínima. El MAPE se denota de la siguiente manera:

En este índice, la distancia entre los datos estimados y los de referencia corresponde al cociente de las diferencias entre la matriz base  y la estimada a  entre la matriz base multiplicada por I/n², donde n es el número de celdas en las matrices.

El Índice de Similitud mide el total de las diferencias de la matriz agrupando las celdas diferentes de 0, lo que indica el comportamiento general de los componentes de la matriz estimada con respecto a la de referencia. El valor del Índice fluctúa entre 0 y 1, donde 0 es la máxima diferencia y 1, la mayor similitud posible; la expresión se plantea como sigue:

donde m es el número de pares coeficientes distintos de 0.

El Índice de Similitud de Leontief Modificado es semejante al de Isard-Romanoff (Isard et al., 1968) y fue empleado por Schaffer y Chu (1969) en su estudio de Utah. Su aplicación se realiza celda por celda en las matrices a comparar:

La interpretación es igual a los anteriores, por lo que el valor del Índice fluctúa entre 0 y 1, correspondiendo la máxima diferencia a 0 y 1 a la mínima en las celdas.

3. Resultados empíricos
3.1. Estructura y funcionalidad económica de la región centro

De acuerdo con los resultados basados en las matrices obtenidas, el patrón de funcionalidad económica de la región centro permanece sin cambios significativos en el 2013 con respecto al 2008, esto significa que la Ciudad de México se mantiene como un núcleo integrador que concentra gran parte de las principales actividades económicas de la región de estudio, en la que predominan los servicios. Por su parte, se encontró que en el estado de México sigue predominando la industria y es núcleo con mayor integración funcional después de la Ciudad de México. Sin embargo, se observan cambios relevantes en la composición de la estructura productiva por sector y rama. Los resultados derivados del análisis de los datos se pueden consultar el cuadro 5.

 

Con base en los cambios observados en el cuadro, puede afirmarse que no son suficientes para sostener la idea de que hay una modificación de estructura productiva en la región debido a que las matrices estimadas muestran que sectorialmente y por rama las economías estatales de la región centro mantienen sus actividades económicas tradicionales y estructura, lo cual indica también que su tecnología no ha variado de forma significativa.

 

3.2. Cuadros de oferta y utilización

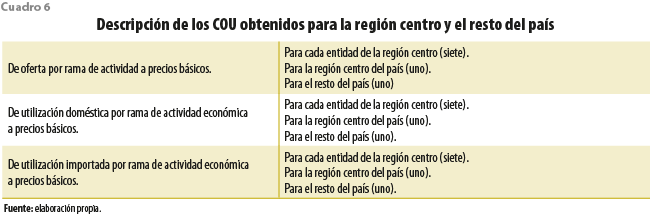
La metodología empleada permitió la construcción de 36 COU_E a nivel rama de actividad económica, las cuales se presentan en el cuadro 6.

 

 

3.3. Matrices de insumo-producto
Se obtuvieron un total de 34 MIP, de las cuales 16 corresponden a la economía doméstica; nueve, a la economía importada; y nueve, a la economía total de las entidades federativas y región centro por sector y rama de actividad económica. En el cuadro 7 se enlistan de acuerdo con su nivel de desagregación sectorial, estatal y regional.

 

 

3.4. Matrices de indicadores
Se obtuvieron 18 matrices de las entidades de la región centro y del resto del país, de las cuales nueve son de coeficientes técnicos y las otras nueve, de directos e indirectos. Estas se enlistan en el cuadro 8.

 

Los resultados descritos en los apartados 3.2, 3.3 y 3.4 se pueden consultar en bit.ly/40uPsN5.

3.5. Análisis del error de eficiencia de la estimación

Los resultados de los índices de eficiencia en el error de estimación de los COU_E y las MIP_E al totalizarse y compararse con los nacionales son favorables. En el caso del MAPE para los vectores de oferta total y los de utilización total, doméstica e importada son iguales a 0, lo cual indica que es una estimación eficiente. Una situación semejante arrojan los del SIMISARD, ya que no presentan diferencias entre las tablas nacional y estimadas, pues no hay discrepancias debido a que el valor del Índice en la oferta total y utilización es igual a 1. Por último, el SIMIL, salvo el valor de la oferta total, arroja diferencias, el resto es cercano a 0 y 1, lo cual indica que no se tiene una desigualdad significativa entre las tablas originales y las estimadas a partir de la suma de los cuadros de las entidades de la región centro y el resto del país, por lo que no son significativos, como se observa en el cuadro 9.

 

 

En general, los resultados que derivan de los cálculos de los índices de similitud aplicados a los COU_N obtenidos de la estimación realizada a partir de la metodología muestran que la eficiencia del error de estimación es adecuada, lo cual ayuda a validar la consistencia de la información que se ha elaborado.

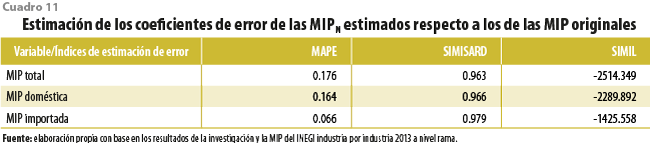
En el caso de las MIP_E de la Ciudad de México, estado de México, Hidalgo, Morelos, Puebla, Tlaxcala y el resto del país, los resultados del MAPE y SIMISARD son cercanos a 0 y 1, lo que indica sus mínimas diferencias con la matriz base de comparación. No obstante, este no es el caso del SIMIL, que arroja valores no aceptables con diferencias significativas, probablemente porque las discrepancias que compara son a nivel de celda considerando la existencia de valores en 0 a partir de la MIP_N que difieren de las matrices estatales y regionales, incluyendo la del resto del país, totalizadas. En el cuadro 11 se presentan los resultados obtenidos. 

De acuerdo con las tablas anteriores, al menos para el caso de los índices MAPE y de Isard-Romanoff, los COU_E y MIP_E obtenidas a partir de la estimación basada en la metodología propuesta y totalizadas para obtener las tablas y matrices nacionales arrojan errores mínimos de estimación si se comparan con las estimadas a nivel nacional, lo cual nos indica que sus resultados son aceptables.

 

4. Conclusiones y reflexiones finales

La aplicación de la metodología RIISIO para la elaboración de los COU_E y las MIP_E a nivel rama de actividad económica estatal y de la región centro han mostrado que se pueden obtener resultados con errores mínimos y consistentes con las tablas y matrices agregadas a escala nacional, con excepción del SIMIL. La validación de los índices MAPE y SIMISARD certifica nuestra estimación; la información generada y la metodología utilizada se considera una herramienta de análisis y producción de estadísticas que permiten analizar la relación entre la demanda y oferta total a nivel de la economía de los estados y de su integración en forma de una región económica.

Esta información desde una perspectiva espacial permite el análisis de la estructura económica y su funcionamiento a escalas subnacional, regional y estatal, lo cual hace posible además llevar a cabo un estudio estructural sobre los cambios en la demanda final y sus repercusiones en la producción y relaciones de insumo-producto, entre la producción y el consumo, precisando la interdependencia y encadenamientos de las ramas y sectores de actividad económica, así como en el análisis de los multiplicadores de empleo y producción, solo por mencionar algunas de las aplicaciones más usuales de los instrumentos de insumo-producto.

La información resultante de este trabajo permite una mejor comprensión del funcionamiento estructural de la economía a niveles regional y estatal y abre la posibilidad de emplear esta herramienta para el análisis y la evaluación de la política económica de las regiones económicas y entidades federativas que las integran, sin la cual se carece de una orientación precisa y se dificulta la solución de problemas concretos.

Por último, cabe aclarar que, a pesar de los alcances y la importancia de esta herramienta analítica, su utilidad no solo permite obtener resultados a niveles estatal y regional comparables con las tablas y cuadros nacionales a través del modelo uniregional; asimismo, se puede utilizar como matriz base para estimar el comercio interestatal e interregional al interior del país e incluso extender su aplicación a escalas intrarregional, multiregional, urbana y local mediante el desarrollo de las aplicaciones y derivaciones metodológicas del método RIISIO que estamos desarrollando.
_____

Fuentes

Asuad, N. “Metodología y resultados de la construcción de matrices estatales de insumo-producto de abajo hacia arriba mediante la elaboración de cuadros de oferta y utilización estatales”, en: Realidad Datos y Espacio Revista Internacional de Estadística y Geografía. 11(2), 2020, pp. 47-89.

_______ Insumo-producto regional. Teoría, metodologías, técnicas y estudios de caso. Colección Economía Regional y Urbana. Volumen tercero. México, UNAM-Facultad de Economía, 2019.

Asuad, N. y Sánchez, J. “A methodological proposal for the construction of a regional input-output matrix using a bottom-up approach and its statistical assessment”, en: Investigación Económica. 75(298), 2016, pp. 3-76.

_______ “Un análisis exploratorio y comparativo entre los enfoques de bottom-up y top-down para una construcción espacial de una matriz regional Input-Output”, en: Revista Mexicana de Economía y Finanzas. 13(2), 2018, pp. 137-174.

_______ “An exploratory and comparative analysis between bottom-up and top-down approaches for a spatialized construction of a regional Input-Output matrix”, en: Revista Mexicana de Economía y Finanzas. 13(2), 2018b, pp. 137-174.

Butterfield, M. y T. Mules. “A testing routine for evaluating cell by cell accuracy in short‐cut regional input‐output tables”, en: Journal of Regional Science. 20(3), 1980, pp. 293-310.

Dávila, A. “Matriz de insumo-producto de la economía de Coahuila e identificación de sus flujos intersectoriales más importantes”, en: Economía Mexicana. Nueva Época. 11(1), 2002, pp. 79-162.

EUROSTAT. Eurostat Manual of Supply, Use and Input-Output Tables. Octava edición. Unión Europea, Eurostat Methodologies and Workingpapers, 2008. ISSN 1977-0375.

Flegg, A., G. Lamonica, F. Chelli M. Recchioni y T. Tohmo. “A new approach to modelling the input–output structure of regional economies using non-survey methods.”, en: Economic Structures. 10(12), 2021 (DE) bit.ly/3shI8re.

Flegg y Tohmo. “A Comm on Tobias Kronemberg´s Construction of Regional Input-output Tables Using Nonsurvey Methods: The Role of Cross Hauling”, en: International Regional Science Review. 36, 2013, pp. 235-257.

Flegg, A. y C. Weber.(2000) “Regional size, regional specialization, and the FLQ formula”, en Regional Studies. 34, 2000, pp. 563-569.

_______ “On the appropiate use of location quotients in generating regional input-output tables: a reply”, en: Regional Studies. 31, 1997, pp. 795-805.

Flegg, A., C. Weber y M. Elliot.(1995) “On the appropieate use of location quotients in generating regional input-output tables”, en: Regional Studies. 29, 1995, pp. 547-561.

Fuentes, N. “Construcción de una matriz regional de insumo-producto”, en: Problemas del Desarrollo. 36(140), 2005, pp. 89-112.

Fuentes, N. y S. Martínez-Pellégrini. “Identificación de clústers y fomento a la cooperación empresarial: el caso de Baja California”, en: Revista Momento Económico. 125, 2003, pp. 39-57.

Fuentes, N. y M. Sastré. “Identificación empírica de sectores clave de la economía sudbajacaliforniana”, en: Frontera Norte. 13(26), 2001, pp. 51-76.

Fuentes, N., A. Brugués, M. Ángeles y J. Sermeño. Estimación de una matriz de insumo-producto y encadenamientos intersectoriales para Baja California Sur. Reporte técnico. La Paz, Baja California Sur, Consejo Nacional de Ciencia y Tecnología (CONACYT), 1999.

García, F., G. Walle y A. Galván. “Identificación de subsectores estratégicos y flujos intersectoriales a partir de la matriz insumo-producto del estado de Tamaulipas, México”, en: Análisis Económico. 35(88), 2020, pp. 209-238.

Germán-Soto, V. “El insumo-producto, diseño y uso en los análisis de economía regional: el caso de Nuevo León”, en: Estudios Económicos. 15(2), 2000, pp. 281-309.

Hewings, G. “The role of prior information in updating regional input-output models”, en: Socio-Economic Planning Sciences. 18(5), 1984, pp. 319-336.

_______ Regional Input-Output Analysis. Reimpresión. Editado por Grant, Ian, Thrall, Repositorio de Investigación WVU, 2020.

Imansyah, M. “An Efficient Method for Constructing Regional Input-Output Table: A Horizontal Approach in Indonesia”, en: 13th International Conference on Input- Output Techniques. Anexo A. Evaluation Methods. Macerata, Italia, 2000.

INEGI. Sistema de Cuentas Nacionales de México: Fuentes y metodologías: año base 2013. México, INEGI, 2018.

Isard, W., T. Langford Jr. y E. Romanoff. Philadelphia region input-output study. Documento de trabajo núm. NASA-CR-95093, 1968.

Jackson, R. “Regionalizing national commodity-by-industry accounts”, en: Economic Systems Research. 10(3), 1998, pp. 223-238.

Kowalesnski, Julia. “Regionalization of National Input-Output tables: Empirical Evidence on the Use of the FLQ Formula”, en: Regional Studies. 49, 2015, pp. 240-250.

Lahr, M. “A strategy for producing hybrid regional input-output tables”, en: 12 Conferencia Internacional de Técnicas de Insumo-Producto. Nueva York, 1998.

_______ “A review of the literature supporting the hybrid approach to constructing regional input–output models”, en: Economic Systems Research. 5(3), 1993, pp. 277-293.

Leontief, W. y A. Strout. “Multiregional Input-Output Analysis”, en: Barna, T. (ed.). Structural Interdependence and Economic Development. Londres, Palgrave-Macmillan, 1963 (DE) bit.ly/45tFrRy.

Martínez-Alpañez, R., D. Buendía-Azorín y M. Sánchez-de-la-Vega. “A New Improvement Proposal to Estimate Regional Input–Output Structure Using the 2D-LQ Approach”, en: Economies. 11(20), 2023 (DE) bit.ly/45zVk9m.

Martins, J., C. Gonçalves, J. Coelho, D. Imori y K. Ando. Construção da Matriz Interregional de insumo-produto para o Brasil: Uma aplicação do TUPI. Núcleo de Economía Regional e Urbana da Universidade de São Paulo, The University of São Paulo Regional and Urban Economics Lab, 2017.

Miller, R. y P. Blair. Input-Output Analysis: Foundations and Extensions. Tercera Edición, Cambridge, Nueva York, Cambridge University Press, 2022.

Pereira-López, X., A. Carrascal-Incera y M. Fernández-Fernández. “A bidimensional reformulation of location quotients for generating input-output tables”, en: Spatial Economic Analysis. 15, 2020, pp. 476-493 (DE) bit.ly/3YJOvQq.

Pereira-López, X, N. Sánchez-Chóez y M. Fernández-Fernández. “Performance of bidimensional location quotients for constructing input–output tables”, en: Journal of Economic Structures. 10, 7, 2021 (DE) bit.ly/3YGgaBC.

Schaffer, W. y K. Chu. “Nonsurvey techniques for constructing regional interindustry models”, en: Papers of the Regional Science Association. 23(1), 1969, pp. 83-101.

Torre, L., J. Alvarado y M. Quiroga. Matrices insumo-producto regionales: una aplicación al sector automotriz en México. Documento de trabajo núm. 12, Banco de México, 2017 (DE) bit.ly/3OZNv7g.

Wade, J. y I. Sarmiento-Barbieri. Input-Output Analysis. CRAN R Project, 2020 (DE) bit.ly/3OJO9Vi.
______________

Anexos