Medición de la tendencia y el ciclo de una serie de tiempo económica, desde una perspectiva estadística

En este trabajo se considera la estimación de tendencias y el análisis de ciclos económicos, desde la perspectiva de aplicación de métodos estadísticos a datos económicos presentados en forma de series de tiempo. El procedimiento estadístico sugerido permite fijar el porcentaje de suavidad deseado para la tendencia y está ligado con el filtro de Hodrick y Prescott. Para determinar la constante de suavizamiento requerida, se usa un índice de precisión relativa que formaliza el concepto de suavidad de la tendencia. El método es aplicable de manera directa a series de tiempo trimestrales, sin embargo, éste se extiende aquí también al caso de series de tiempo con periodicidad de observación distinta de la trimestral. Palabras clave: curva suave, estimación óptima, filtro de Hodrick y Prescott, filtro de Kalman, modelos de series de tiempo, métodos estadísticos, precisión relativa.		This work deals with trend estimation and business cycle analysis, with emphasis on the application of statistical methods to economic time series data. The suggested statistical procedure allows one to fix a desired percentage of trend smoothness and is linked to the Hodrick-Prescott filter. An index of relative precision, coming out from a formal definition of trend smoothness, is used to decide the smoothness constant involved. This method is directly applicable to quarterly series, but its use is extended with ease to time series with frequencies of observation other than quarterly. Key words: Hodrick-Prescott filter; Kalman filter; optimal estimation; relative precision; smooth curve; statistical methods; time series models.

 

1. Introducción

El estudio de los ciclos económicos se puede enmarcar dentro de la teoría de los ciclos de negocios siempre que se subrayen las causas y la naturaleza de las fluctuaciones económicas. Los primeros estudios realizados con este enfoque fueron desarrollados durante las décadas de los 30 y los 40 en el National Bureau of Economic Research (NBER) de Estados Unidos de América (EE.UU.) por investigadores como A. F. Burns y W. C. Mitchell, quienes desarrollaron un programa de trabajo para documentar de manera empírica los ciclos observados en EE.UU. y en otros países.

Una cronología de los ciclos comúnmente aceptada para EE.UU. se basa en la siguiente definición del ciclo de negocios: “…un tipo de fluctuación que se encuentra en la actividad económica global de las naciones (…) un ciclo consiste de expansiones que ocurren casi al mismo tiempo en diversas ramas de la actividad económica, seguidas en general y similarmente por recesiones, contracciones y recuperaciones que se combinan en la fase de expansión del ciclo siguiente…” (Burns y Mitchell, 1946, p. 3). Una de las conclusiones a las que llegaron dichos autores es que los ciclos económicos son eventos recurrentes (aunque no con regularidad periódica), con características similares en el tiempo y en diferentes naciones. Una lista de fechas de referencia, a partir de 1854, para los ciclos de negocios de EE.UU. identificados por el NBER se encuentra en el sitio bit.ly/4fk9Ash.

Durante la década de los 80 se vio la necesidad de estudiar los ciclos reales de la economía a partir de la idea de que los movimientos de las variables reales mueven en gran medida la economía de un país. De hecho, en la actualidad no sólo se hace referencia a los ciclos macroeconómicos, sino que también se realizan estudios de los ciclos que presentan algunas industrias específicas para desarrollar estrategias de producción e inversión apropiadas para tales industrias. Esto se debe a que los ciclos industriales muchas veces presentan patrones distintos a los mostrados por los ciclos de negocios; por ejemplo, Berman y Pfleeger (1997) encontraron que no todas las ramas industriales registran fluctuaciones correlacionadas con las de la economía agregada, pues industrias como la farmacéutica y de salud pueden mostrar crecimiento durante las recesiones.

Adicionalmente, debe reconocerse que las naciones desarrolladas tienen mayor estabilidad económica que los países en desarrollo y, por ello, el estudio de los ciclos económicos es de mayor relevancia en estos últimos, ya que para ellos es más necesario plantear políticas económicas que tengan en cuenta explícitamente las fases del ciclo; por ejemplo, es claro que los ciclos económicos de EE.UU. afectan a México, lo cual —aunado a los asuntos internos de carácter político, social y financiero de nuestro país— hace que las fluctuaciones económicas sean más volátiles aquí que en Estados Unidos de América. Desde luego, las herramientas analíticas que se utilicen en México deben ser tan buenas como las usadas en los países desarrollados, pero es deseable, incluso, contar con elementos adicionales para enfrentar de mejor manera los retos que impone el análisis de los datos generados en México.

Es importante notar que los datos requeridos para realizar un análisis de ciclos económicos se presentan en forma de series de tiempo, es por ello que la referencia a modelos para series de tiempo se vuelve imperativa al referirse a este tipo de análisis. Aun cuando la teoría económica de los ciclos no pretende explicar las fluctuaciones de las series de manera individual, sino para un conjunto de ellas, el análisis estadístico sí conviene realizarlo en un principio para cada serie en forma univariada (una introducción a la teoría y aplicaciones de los modelos lineales para series de tiempo univariadas se presenta en Guerrero, 2009). En consecuencia, el estudio de los ciclos económicos integra tanto elementos de teoría económica como de análisis puramente estadístico de series de tiempo.

El enfoque del presente trabajo es de metodología estadística más que de carácter económico, es por ello que se enfatizará el método estadístico que se usa para distinguir y medir los dos componentes esenciales que se supone integran la serie de tiempo dentro del ámbito del análisis de ciclos económicos. Estos componentes son: a) la tendencia, que debe mostrar un comportamiento suave, asociado con el patrón de largo plazo subyacente en la serie y b) el ciclo, el cual se define como diferencia entre los datos observados y su respectiva tendencia.

Lo que resta del artículo tiene la siguiente estructura: la sección que sigue presenta el filtro de Hodrick y Prescott (1997), originalmente aparecido en 1980 en un documento no publicado, el cual constituye el método empleado con mayor frecuencia para descomponer una serie (previamente desestacionalizada) en sus componentes de tendencia y ciclo. Dicho filtro requiere de la elección de un parámetro de suavizamiento, al cual se le asigna por lo común un valor estándar, en función de la periodicidad de observación de la serie. En este trabajo, en cambio, se sugiere utilizar el método propuesto por Guerrero (2008), con el cual se puede medir y controlar el porcentaje de suavidad deseado para la tendencia. La sección 3 se ocupa del problema de ajustar la constante de suavizamiento en función de la frecuencia de observación de la serie, es decir, para encontrar valores de las constantes que sean equivalentes, en tanto que produzcan el mismo porcentaje de suavidad para una serie agregada (trimestral) y la serie desagregada de la misma variable (mensual). En la 4 se muestra una aplicación del método para realizar análisis de ciclos económicos con series de México; el objetivo de esta aplicación no pretende más que ilustrar las implicaciones que conlleva el trabajar con series de tendencia que tengan distintos porcentajes de suavidad. La 5 concluye con algunos comentarios finales y recomendaciones.

2. Filtro de Hodrick y Prescott

El sustento del análisis de ciclos económicos radica en el supuesto de que las series de tiempo económicas están compuestas por elementos que no son observables directamente, pero cuya existencia se acepta debido a que la teoría económica así lo indica. Los modelos de series de tiempo que surgen en tales condiciones se denominan de componentes no-observables y en el caso del análisis de ciclos económicos tienen como elementos constitutivos básicamente a la tendencia, entendida como el movimiento suave, de largo plazo, subyacente en la serie, y al ciclo, que se obtiene como diferencia entre los datos de la serie observada (previamente desestacionalizada) y la respectiva tendencia. El problema que se enfrenta en la práctica es cómo distinguir y separar estos componentes de la serie observada, que se supone la conforman, pero que no son visibles por separado.

Una idea simple consiste en suponer que el comportamiento de la tendencia es de tipo exponencial, de manera que al tomar logaritmos de la serie se observaría una línea recta en la gráfica de la serie contra el tiempo. Si éste fuera el caso, al hacer la regresión del logaritmo de la serie sobre el tiempo se obtendría la tendencia estimada y, por diferencia respecto a los datos observados, el componente cíclico estimado. Debe notarse que el supuesto de tendencia lineal determinista no es intrascendente, pues implica que la serie observada tiene un comportamiento estacionario en tendencia, lo cual ha sido puesto en duda desde que apareció el trabajo de Nelson y Plosser (1982).

En lugar de suponer una tendencia determinista, pudiera pensarse que la serie es estacionaria en diferencias, lo cual implica que la serie tiene una raíz unitaria, por lo que al tomar diferencias del logaritmo de la serie se cancelaría la tendencia y se obtendría el ciclo de manera inmediata. La cuestión a resolver es, entonces, cuál de estas dos representaciones es más apropiada para una serie determinada. Este dilema no ha sido resuelto por completo y ha surgido una gran cantidad de literatura sobre el mismo (un texto que presenta el tema con diversos enfoques, tanto para el caso univariado como el multivariado, es el de Maddala y Kim, 1998). Un problema grave que se enfrenta al eliminar la tendencia con un método que pudiera ser inapropiado es que se podrían generar ciclos de carácter espurio y el análisis carecería de validez.

Por otro lado, el enfoque basado en filtros está motivado por la idea de que una definición matemática clara de lo que constituye un ciclo pudiera conducir a un procedimiento que limpie apropiadamente a la serie de fluctuaciones que no corresponden al movimiento periódico dentro de un cierto rango de duración de los ciclos. Para ello, se cuenta con la cronología desarrollada por el NBER para EE.UU., donde se encuentra que el ciclo más corto (de cresta a cresta) es de seis trimestres y el más largo, de 39 trimestres, además de que 90% de los ciclos no duran más de 32 trimestres (véase Stock y Watson, 1999, p. 11) por lo cual, un rango de duración de los ciclos que abarque a lo más ocho años pudiera ser razonable.

Dentro de este contexto surgió el filtro de Hodrick y Prescott (1997), previamente utilizado en Astronomía, Actuaría y Balística, al cual se hará referencia de aquí en adelante como filtro HP, cuya característica fundamental es que depende sólo de una constante, que permite regular el grado de suavidad de la tendencia. La elección de dicha constante es básicamente arbitraria, pero ellos decidieron elegirla de manera tal que el filtro fuera tal que produjera un componente de tendencia libre de fluctuaciones cíclicas (ya que cancela todas las frecuencias menores a ocho años).

El argumento esencial para el uso de este filtro lo expuso Prescott (1986) al mencionar que “…si los hechos característicos del ciclo de negocios fuesen sensibles al método usado para cancelar la tendencia, habría un problema; pero los hechos clave no son sensibles al procedimiento si la curva de tendencia es suave…”; por lo tanto, lo que en realidad importa es lograr una suavidad adecuada para la serie en estudio.

Cabe notar, también, que algunos autores han escrito en contra del uso indiscriminado del filtro HP, entre ellos se encuentran Cogley y Nason (1995) y Park (1996), quienes concluyen que el filtro HP suele inducir ciclos de tipo espurio. En contraste, Pedersen (2001) argumentó que la causa de tal problema es la definición misma del efecto espurio y demostró que el filtro HP, ya sea con el valor típico λ = 1600 o con una elección óptima de dicha constante que minimice las distorsiones del filtro, se comporta mejor que otras alternativas; asimismo, Maravall y del Río (2007, Appendix A) subrayaron que “…En general, el concepto en sí mismo de espurio es cuestionable dentro del contexto de filtros diseñados en forma ad hoc: el filtro simplemente produce lo que fue diseñado para producir, sin referencia a un modelo…”; en el caso del presente trabajo, lo que se va a pedir del filtro HP es que produzca un cierto porcentaje de suavidad fijado de antemano.

2.1 Deducción del filtro HP

En principio, conviene decir que por filtro se entenderá cualquier operación que se efectúe sobre una cierta serie original {y_t} para obtener una nueva serie filtrada, que, en el presente caso, será la tendencia estimada . El filtro HP no requiere, propiamente, de la construcción de un modelo estadístico, lo cual es indispensable con otros enfoques basados en modelos. El planteamiento formal que da origen al filtro HP postula que, si se cumple la relación expresada en forma de modelo de componentes no-observables

(2.1)

donde y_t representa la variable observada en el tiempo t, mientras que τ_t y η_t son sus respectivos componentes de tendencia y ciclo, entonces la tendencia se puede estimar al resolver el problema de minimización de la función

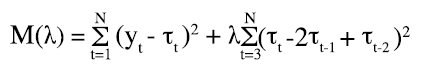(2.2)

donde λ > 0 es una constante que penaliza la variabilidad de la tendencia. Si se escribe

(2.3)

se observa que al hacer λ → 0, la fidelidad a los datos observados (F) se enfatiza al extremo de que τ_t → y_t para toda t. En cambio, si λ → ∞, la suavidad (S) se maximiza de manera tal que la tendencia sigue el comportamiento dictado por la ecuación τ_t – 2τ_t-1+ τ_t-2 = 0, que corresponde a una línea recta. Con esto se aprecia que λ juega un papel crucial para decidir el grado de suavidad para la tendencia.

El problema de minimización anterior puede escribirse en notación matricial con la función

(2.4)

donde aparecen los vectores y = (y₁,…,y_N)’ y τ = (τ₁,…,τ_N)’. Además, el apóstrofo indica transposición y K es la matriz de dimensión (N-2) x N, dada por

(2.5)

y de esta manera, la solución resulta ser

(2.6)

El valor λ = 1600 se elige por lo común al aplicar el filtro HP a series trimestrales, debido a que fue éste el valor utilizado por Hodrick y Prescott en su estudio de diversas series macroeconómicas de EE.UU., para el periodo 1950-1979. Las razones para esta elección serán mencionadas más adelante.

Por otro lado, nótese que es necesario invertir una matriz de dimensión N x N para obtener el vector T̂, lo cual puede ser causa de inestabilidad e imprecisión en el cálculo numérico de la solución, cuando N es grande. Así pues, con este enfoque se tiene la ventaja de apreciar de manera explícita los roles de λ , F y S, pero no necesariamente se obtiene una herramienta eficiente de cálculo numérico de la tendencia. Para ello, es preferible emplear el filtro de Kalman con suavizamiento, que sólo requiere invertir una matriz de 2 x 2, independientemente del tamaño de la serie, N. Por consiguiente, ésta es la forma como se propone aplicar el filtro HP en este trabajo.

Los resultados del filtro HP pueden apreciarse en comparación con los que surgen del procedimiento de ajuste estacional X-12-ARIMA (para una descripción de este procedimiento, véase Findley et al., 1998). La figura 1 presenta cuatro gráficas, tomadas del trabajo de Guerrero (2008), que permiten comparar distintas estimaciones de la tendencia para la serie del PIB real trimestral de México, previamente desestacionalizada. La gráfica (a) muestra la tendencia que surge del paquete X-12-ARIMA, con las opciones automáticas. En la gráfica (b) se presenta la tendencia que produce el filtro HP aplicado con el valor tradicional λ = 1600 y en las gráficas (c) y (d) aparece la tendencia que se obtiene con los valores λ = 1 y λ = 199. La suavidad de la tendencia es parecida en los casos (a) y (c), con lo cual se deduce que el filtro HP puede producir resultados semejantes a los del procedimiento X-12-ARIMA. Sin embargo, la tendencia difiere sustancialmente en los otros casos. Así, elegir de la manera más objetiva el valor de la constante λ es necesario para lograr una estimación apropiada de la tendencia.

2.2 Constante de suavizamiento

Hodrick y Prescott (1997) eligieron el valor de λ, en el supuesto de que las variables aleatorias η_t = y_t– τ_t y Ɛ_t = τ_t – 2τ_t-1 + τ_t-2 se distribuyen como N(0, σ_η² ) y N(0, σ_Ɛ² ), respectivamente, y son independientes. Además, ya que la serie en estudio, {y_t}, se expresa comúnmente en logaritmos, y_t – y_t-1 representa una tasa de crecimiento. En consecuencia, el cambio en la tasa de crecimiento de la tendencia y el ciclo se suponen procesos de ruido blanco gaussianos y la constante resulta ser λ = σ_η² /σ_Ɛ² , por lo cual se le puede interpretar como una medida relativa que pondera suavidad y ajuste. De hecho, en el caso σ_Ɛ² = 0 se obtendría como tendencia una línea recta, con pendiente constante (su varianza es cero). En cambio, si σ_η² = 0, entonces el ciclo es la constante cero y se logra un ajuste perfecto a los datos, pues se obtiene τ_t = y_t para t =1,…,N.

En su estudio, Hodrick y Prescott consideraron que la tasa de crecimiento tendencial se movía lentamente y fijaron a priori los valores de las desviaciones estándar como: 1/8 de 1% en un trimestre para el componente de tendencia (σ_Ɛ = 1/8) y 5% para el componente cíclico (σ_η = 5), de donde surgió el valor λ =σ_η² /σ_Ɛ² = 1600. Posteriormente, analizaron la sensibilidad de sus resultados ante esta elección y consideraron que no había razón para dudar de ellos. A partir de entonces, dicho valor se volvió el estándar a usar con el filtro HP. Sin embargo, debe ser claro que esta selección de λ surgió de consideraciones juzgadas apropiadas por Hodrick y Prescott dentro del contexto de su estudio, con series trimestrales y de la longitud empleada por ellos. Desde luego, si cambia la periodicidad de observación o la longitud de las series, tal valor debería también cambiar. Una manera de hacer esto se logra con base en el modelo estadístico subyacente en el filtro HP y el enfoque que se describe a continuación.

Debe mencionarse un procedimiento propuesto por Kaiser y Maravall (2001, Chap. 7) que tiene en cuenta las bondades del enfoque estadístico basado en modelos univariados de series de tiempo del tipo ARIMA (auto-regresivo, integrado y de promedios móviles, véase Guerrero, 2009) y las combina con la idea de elegir el valor de λ que conduzca a resultados interpretables en el contexto del análisis económico que se realice. De hecho, estos autores propusieron nuevamente seleccionar la constante de suavizamiento fijando la longitud del periodo sobre el cual se desea medir la actividad cíclica y proporcionaron un cuadro (Table 5.11) para ser usado con series trimestrales, donde se relaciona el periodo en años con un valor aproximado de λ.

2.3 Elección de λ con base en la suavidad deseada

Supóngase que el modelo formado por las expresiones

(2.7)

es válido para t = 1,…,N, con {η_t} y {Ɛ_t } ruidos blancos no correlacionados entre sí, ambos con media cero y con varianzas respectivas σ_η² y σ_Ɛ² . Entonces, se sigue que

(2.8a)

y

(2.8b)

Además, como E(Ɛη ‘) = 0, se obtiene

(2.9)

por lo tanto, el método de mínimos cuadrados generalizados produce el siguiente estimador lineal con error cuadrático medio (ECM) mínimo (la justificación del uso de este método para estimar el vector de variables aleatorias τ, en lugar de parámetros constantes, aparece en Guerrero, 2007)

(2.10)

cuya matriz de ECM está dada por

(2.11)

La matriz de precisión del estimador, Γ^-1, está formada por la suma de dos precisiones, σ^-2_ηI_N correspondiente al modelo (2.8a) y σ_Ɛ^-2 K’ K asociada con el modelo (2.8b). Este hecho fue explotado por Guerrero (2008) para proponer una medida que cuantifica la proporción de σ_Ɛ^-2 K’ K en Γ^-1, donde las matrices involucradas son definidas positivas y de dimensión N x N. Dicha medida es

(2.12)

y tiene las propiedades siguientes: a) toma valores entre cero y uno, b) es invariante bajo transformaciones lineales no-singulares de la variable en cuestión, c) se comporta linealmente y d) es simétrica, en el sentido de que Λ(σ_Ɛ^-2 K’ K; Γ) + Λ(σ_η^-2I_N; Γ) = 1. Entonces, para cuantificar la proporción de precisión atribuible a la suavidad, que introduce el uso de (2.8b) en el modelo, se considerará como índice de precisión relativa atribuible a la suavidad o en breve, índice de suavidad, a

(2.13)

con

Como puede observarse, este índice depende (en forma monótona creciente) sólo de los valores de λ y de N, pues la matriz K está fija. Además, debido a la estructura de la matriz I_N + λK ‘ K, se sabe que dos de sus valores propios son cero y los restantes cumplen con , por lo cual tr[(I_N+λK’ K)^-1] = (1+ λe₁)^-1 +…+ (1+ λe_N-2)^-1 + 2, de donde se deduce que

(2.14)

Conviene ahora multiplicar este índice por 100 para interpretarlo como porcentaje de suavidad logrado con el filtro empleado; en tal caso, se escribe 100S(λ; N)% o, simplemente, S%; la utilidad fundamental de este índice, dentro del marco de la estimación de tendencias, radica en que puede fijarse desde un principio un cierto porcentaje de suavidad deseado para la curva suave que represente a la tendencia y, con ayuda de la expresión para S(λ; N), deducir entonces el correspondiente valor de la constante λ.

Para realizar análisis de ciclos económicos, el filtro HP debe aplicarse a la serie desestacionalizada, pues de otra manera se confundirán los efectos cíclicos con los de la estacionalidad, ya que ambos son periódicos, aunque los estacionales son recurrentes cada año y los cíclicos no tienen por qué ser de regularidad periódica. En cambio, si la tendencia deseada para la serie es igual o mayor que 65%; entonces, la serie puede o no estar previamente desestacionalizada, pues la tendencia que resulte no se verá afectada por los efectos estacionales. Esto lo garantizan los resultados de Kaiser y Maravall (2001, Table 5.11), los cuales indican que al usar se cancelan las fluctuaciones con duración menor a los dos años (dentro de las cuales se encuentran los efectos estacionales) y con esos valores de λ se obtienen suavidades iguales o mayores que 65%; también, debe recordarse que si son varias series a las que se aplicará el filtro HP, en todas ellas debería usarse el mismo criterio de suavidad para hacer comparables los resultados; conviene, asimismo, resaltar el hecho de que conforme el tamaño de muestra cambia, aun para la misma serie, debe cambiarse el valor de la constante de suavizamiento con el fin de mantener fijo el porcentaje de suavidad en la tendencia. No obstante, los cambios en λ tendrán efectos en la suavidad de una serie sólo cuando el tamaño de muestra cambie de manera sustancial (consúltense los cuadros llamados Table 1 y Table 2 en Guerrero, 2008, para ver la relación entre el porcentaje de suavidad y los valores de λ y de N).

Como ejemplo de la aplicación del procedimiento señalado, considérese la serie del PIB trimestral que se mostró en la figura 1, la cual contiene N = 97 datos, pues cubre el periodo de 1980:01 a 2004:01. Si la suavidad deseada para la tendencia es de 90%, la correspondiente constante de suavizamiento que se obtiene es λ = 199 y con ella se produce el resultado que se muestra en la gráfica (d) de la figura 1. En cambio, cuando el valor utilizado es λ = 1, como sucede en la gráfica (c) de dicha figura, la suavidad que se logra es de 60.7%, mientras que el valor λ = 1600 produce 93.9% de suavidad. Además, en las gráficas de la figura 1, el filtro HP se aplicó a la serie del PIB desestacionalizada y en logaritmos. Posteriormente, a la tendencia resultante se le aplicó el antilogaritmo para expresarla en la escala de la variable original. En contraste, en la figura 2 se muestran los resultados de aplicar el filtro HP al PIB sin desestacionalizar y sin logaritmos, con dos diferentes porcentajes de suavidad para la tendencia.

Al comparar la tendencia mostrada en la gráfica (a) de la figura 2, con la de la figura 1, se corrobora el hecho de que la desestacionalización no afecta al cálculo de la tendencia, cuando la suavidad es, al menos, de 65%; la suavidad en la gráfica (a) es mayor que en la gráfica (b); por ello, la tendencia reacciona con lentitud ante los movimientos inesperados de la serie, lo cual podría considerarse como una visión conservadora. Este tipo de argumentos podrían ayudar a decidir el porcentaje de suavidad que se desee obtener al aplicar la metodología propuesta. Por último, es importante advertir que el método propuesto está enfocado a estimar el componente de tendencia de una serie de tiempo trimestral y, como diferencia respecto a los datos observados, se obtiene el ciclo estimado. A continuación se muestra cómo obtener la constante de suavizamiento apropiada para lograr un cierto porcentaje de suavidad, en series que no sean trimestrales.

3. Elección de λ para series no trimestrales

Cuando la serie de tiempo para la cual se desea estimar su tendencia no es trimestral, los valores de λ que proporcionó Guerrero (2008, Table 1 y Table 2) no son aplicables. Para entender el porqué de esta afirmación, supóngase que el periodo de observación de la serie cubre cinco años, del 2004 al 2008; ello implica que se cuenta con N = 20 datos trimestrales o, de manera equivalente, con “N” = 60 datos mensuales. Así, aunque el comportamiento de largo plazo de la serie debería ser esencialmente el mismo en los datos mensuales, trimestrales y anuales, los cuadros mencionados conducirían a elegir valores de λ distintos para la misma suavidad y producirían tendencias distintas. El problema ocurre por no tener en cuenta que los datos de la serie mensual guardan una relación estrecha con los trimestrales y con los anuales. Este hecho fue reconocido por Maravall y del Río (2007), quienes propusieron diversas soluciones para encontrar valores de la constante de suavizamiento que produjeran resultados equivalentes en datos con diferentes periodicidades de observación. En particular, ellos decidieron elegir el valor de λ de tal manera que se preserve el periodo del ciclo para el cual la ganancia del filtro HP respectivo es 1/2. Esto es consistente con la propuesta de Kaiser y Maravall (2001), en tanto que el objetivo de aplicar el filtro HP sea exclusivamente analizar ciclos económicos.

Por otro lado, es común que los analistas cambien el valor de la constante λ en función de la periodicidad de observación de la serie, para ello se define k como el número de datos desagregados que hay entre dos datos agregados; por ejemplo, en un trimestre hay k = 3 datos mensuales. Así, se acostumbra simplemente multiplicar a λ por k² (de esta forma, el valor 1600 para una serie trimestral conduce al valor 14400 para una serie mensual). Otra propuesta para obtener la constante apropiada para la serie agregada es la de Ravn y Uhlig (2002), cuyo resultado principal establece que

(3.1)

de esta manera, el valor λ* = 1600 para una serie trimestral se convierte en λ_k,RU = 129600 para la serie mensual. Como puede apreciarse, la diferencia entre 14400 y 129600 es demasiado grande y no hay una razón generalmente aceptada que indique cuál es preferible. La idea de fijar la suavidad deseada ayuda en esta decisión.

Para los fines de este trabajo, la elección de λ para series que no sean trimestrales debe ser tal que produzca el mismo porcentaje de suavidad que se obtiene con la constante correspondiente para datos trimestrales. Lo que se propone hacer es determinar el valor de λ asociado con el filtro HP, dependiendo de la naturaleza de la serie, es decir, del tipo de operación que se requiere efectuar para agregar los datos con mayor frecuencia de observación {y_t}, digamos mensuales, a datos observados con menor frecuencia {y^*_T}, digamos trimestrales. La agregación se supondrá del tipo lineal, que es lo común, o sea

(3.2)

las constantes c_j definen el tipo de agregación, de manera que c₁ =…= c_k= 1 se usan para agregar una serie de flujos, c₁ =…= c_k = 1/k para un índice o para flujos anualizados (en estos casos se dirá que la serie es de flujos). En cambio, c₁ = 1, c₂ =…= c_k ó c₁ =…= c_k-1= 0, c_k = 1 se usan cuando la serie es de saldos, en cuyo caso la serie agregada se genera a partir de la desagregada mediante muestreo sistemático.

El modelo que justifica el filtro HP para la serie agregada es de la forma (2.8), o sea

(3.3a)

y

(3.3b)

con E( Ɛ*η*’)=0, donde el asterisco denota que la variable es agregada. Igual que antes, ahora también se obtiene

(3.4)

donde es el número de datos agregados y └x ┘ es la función mayor entero menor o igual que x. Aunque el modelo utilizado y el filtro HP resultante para la serie agregada sean de la misma forma que los correspondientes para la serie desagregada, el filtro HP no se preserva ante la agregación, es decir, al agregar los componentes {T̂_t} y {η̂ _t} estimados con la serie desagregada, no se obtienen los mismos componentes {T̂^*_T} y {η̂ ^*_T} estimados directamente con la serie agregada. Sin embargo, es factible encontrar un valor de λ* para datos agregados que sea equivalente a la constante λ para los datos desagregados, en el sentido de que la estimación de los componentes obtenidos de manera directa y de forma indirecta sean, prácticamente, indistintos.

El método a utilizar en este trabajo consiste en igualar las autocovarianzas de los modelos subyacentes en los filtros HP agregado y desagregado. La derivación matemática sigue los argumentos de Guerrero (2005) y el resultado al que se llega es una combinación lineal del de Ravn y Uhlig (2002) con el tradicional. Para pasar de datos desagregados a datos agregados se debe usar (3.5), mientras que (3.6) se usa con el fin inverso

(3.5)

(3.6)

Para ilustrar el uso de estos resultados, a continuación se estima la tendencia del PIB mensual (obtenido como desagregación del PIB trimestral). Para obtener el valor de equivalente a la constante λ* que se usa con la serie trimestral del PIB, como el periodo de observación mensual va de 1980:01 a 2004:03, se tiene que los N = 291 meses en consideración equivalen a n = 97 trimestres y que la serie es de flujos. En consecuencia, la fórmula por utilizar es = 3.901961+70.411765λ* de tal manera que para obtener S% = 90% se requiere usar λ* = 199.38 y para lograr S% = 80%, el valor debe ser λ*= 12.28. Estas constantes conducen a los valores = 14402 y = 869.12, respectivamente. Las tendencias que se obtienen con el filtro HP se muestran en la figura 3. Al comparar estas gráficas con las de la figura 2, se concluye que tendencias con idénticas suavidades muestran igual comportamiento, sin importar la periodicidad de observación de los datos.

Para corroborar que la tendencia se comporta esencialmente igual, sin importar la periodicidad de observación de la serie, también se calculó la tendencia para el PIB anual con los porcentajes de suavidad usados de manera previamente. Ya que se cuenta con n = 24 años completos (de 1980 al 2003), el número de trimestres resulta ser N = 96, con lo cual las constantes de suavizamiento para S% = 90% y S% = 80% son λ = 199.86 y λ = 12.29.

Al usar la relación = -0.057170 + 0.004531λ se obtienen los valores =0.8484 y λ * ₄ = -0.0015 ≈ 0.00001 (debido a que sólo se permiten valores positivos) para las suavidades respectivas. Con dichas constantes se obtienen las tendencias de la figura 4, donde se demuestra de forma empírica la validez de la afirmación hecha con anterioridad. Además, al usar una constante de suavizamiento prácticamente igual a cero, la tendencia reproduce a las observaciones.

4. Análisis de ciclos de la economía mexicana

El objetivo de la presente sección es ilustrar los resultados que surgen al usar el procedimiento para elegir la constante de suavizamiento que produzca un porcentaje de suavidad fijado de antemano, dentro del contexto de un análisis de ciclos económicos, propiamente dicho. Este apartado se basa en el trabajo de Colín (2008), donde se muestra con mucho más detalle y extensión, la aplicación que aquí aparece, así como otra aplicación completa a diversas series de México y de Estados Unidos de América. Aquí sólo se resumen algunos de los resultados obtenidos por él. Las series a utilizar son trimestrales y cubren el periodo del primer trimestre de 1950 al cuarto trimestre del 2006, por lo cual se cuenta con N = 228 observaciones. El máximo nivel de suavidad que se puede lograr está dado por 1-2/N = 0.99. Por ello, es razonable proponer como porcentajes de suavidad S% = 90% y S% = 95%; a partir de estos porcentajes se deducen los valores λ = 177 y λ = 3016, respectivamente. Con fines comparativos se usará también el valor λ = 1600, que para este tamaño muestral produce tendencias con suavidad aproximada de 94 por ciento.

Se sigue el esquema establecido por Hodrick y Prescott (1997) en su estudio, y es por esto que se usan algunas de las series de la economía norteamericana que ellos emplearon. El grupo de series se refiere al producto interno bruto real y sus componentes de demanda agregada, esto es,

La fuente de los datos es el Banco de Información Económica del INEGI en el sitio bit.ly/3SliuMg. En la figura 5 se muestran las tendencias que se obtienen con los distintos valores de la constante de suavizamiento, en la escala logarítmica; por lo cual, las tendencias se asemejan a una línea recta. Es difícil distinguir a simple vista diferencias notorias en las tendencias y, como era de esperarse, al aumentar el porcentaje de suavidad la tendencia se asemeja más a una línea recta, y discrepa más de la serie original.

Los ciclos que se obtienen con las distintas elecciones de la constante de suavizamiento ensayadas se presentan en la figura 6. Ahí se observa que el componente cíclico con mayor varianza surge con λ = 3016, mientras que λ = 177 produce un ciclo que fluctúa menos alrededor de cero. En lo que sigue, al hacer referencia a una variable se debe entender una referencia a su ciclo.

Así como se obtuvo el componente cíclico para el PIB, se obtuvieron los componentes cíclicos para cada una de las variables del grupo. La variabilidad de la serie es una de las características que se estudian al realizar análisis de ciclos, y la medida de variabilidad del ciclo que se usa es la desviación estándar, mientras que la co-variabilidad con el PIB se mide con el coeficiente de correlación lineal. Estas medidas se calcularon para la primera y la segunda mitad de la serie, así como para la serie completa, con el fin de observar la estabilidad de estas medidas en el tiempo. Debe subrayarse que las tendencias que se obtienen con el mismo grado de suavidad son comparables, aunque tengan tamaños de muestra diferentes. Para lograr la comparabilidad, deben utilizarse constantes de suavizamiento apropiadas para la mitad de la serie, o sea, para N = 114. En tal situación, las constantes de suavizamiento correspondientes a 90, 94 y 95% de suavidad son, respectivamente, λ = 194, λ = 1780 y λ = 3652.

Además, para entender mejor la co-variabilidad, se usan otras tres medidas, las primeras dos son la correlación de la serie con el PIB un periodo atrás y uno adelante. Esto se hace así porque una serie puede no estar correlacionada con el PIB contemporáneo, pero sí estarlo con el del periodo anterior o el siguiente. También, puede darse el caso contrario, en el que haya una correlación contemporánea muy fuerte, pero la correlación con el periodo anterior o siguiente sea casi nula. La tercera medida a usar es el coeficiente de determinación, R², de la regresión

(4.1)

Donde z_j representa cada una de las variables en el grupo. Para estudiar esta medida, se utiliza un cociente cuyo numerador es la R² de la regresión (4.1) y el denominador es la R² de la misma regresión, con la diferencia de que para esta última los valores estimados de β_j,i no tienen que ser iguales para la regresión de la primera y de la segunda mitad de la serie. A este cociente, que toma valores entre 0 y 1 se le denomina medida de estabilidad. Uno de sus casos límite surge cuando los coeficientes β_j,i no cambian entre la primera y la segunda mitad, aun cuando se les permita hacerlo y, por lo tanto, la R² es igual para los dos casos. Otro ejemplo límite es cuando cambian los coeficientes y hacen que la R² pase de 0 a positiva.

Otra característica que se documenta es la desviación estándar de las series, como proporción de la desviación estándar del PIB, con el fin de ordenar las series según el número de veces que su desviación estándar representa la del PIB y observar si este orden se mantiene para los diferentes niveles de suavidad. Para cada λ también se presenta un cuadro que muestra la correlación de la serie con el PIB en orden ascendente, esto se hace con el fin de observar si el orden se mantiene para los diferentes valores de λ. Los resultados del análisis de los ciclos económicos para los componentes de la demanda agregada que aparecen en Colín (2008) fueron condensados en los cuadros que se presentan a continuación.

El cuadro 1 contiene la desviación estándar y la correlación con el PIB (para la serie completa y cada una de sus mitades); en éste se observa que las desviaciones estándar más bajas en los tres casos (λ = 177, λ = 1600 y λ = 3016) corresponden al consumo de servicios y los bienes no durables, mientras que el componente con mayor desviación estándar es el de la inversión fija total de tipo residencial. Las primeras dos variables son representantes del consumo y la tercera, de la inversión. La desviación estándar del PIB y todos los componentes de la demanda agregada (con excepción de la inversión fija total en estructuras y el consumo de servicios con λ = 177) son mayores en la primera mitad de la serie (1950:1–1978:3) que en la segunda mitad (1978:4 – 2006:4).

También, se observa en el cuadro 1 que las correlaciones con el PIB son positivas en general y relativamente grandes para todos los componentes, excepto para las variables gubernamentales (gasto agregado, federal, estatal y local) con la única correlación negativa, -0.128 para el gasto de gobiernos estatales y locales, aun cuando al observar la correlación por mitades de la serie los valores negativos son para el gasto agregado del gobierno y el del gobierno federal.

En el cuadro 2 aparecen la intensidad de asociación con el PIB y la medida de estabilidad.

En el caso λ = 177, el cuadro 2 permite apreciar que la R² de la regresión es relativamente alta para todos los componentes, excepto para la inversión en estructuras y las tres variables gubernamentales. Los valores más bajos de la medida de estabilidad también corresponden a estas variables, lo que implica correlaciones bajas tanto para este periodo como para los dos periodos anteriores y siguientes. La medida de estabilidad es muy cercana a la unidad en los otros casos. Por el lado de la correlación cruzada con el PIB del periodo pasado, ésta muestra su valor más grande para las variables de inversión (con excepción de la residencial) y es interesante que para las variables gubernamentales esta correlación es mayor a la que existe con el PIB del mismo periodo. La correlación con el PIB del siguiente periodo es positiva para todos los casos, menos para las variables gubernamentales.

Cuando se considera λ = 1600, también se observa que la R² de la regresión es relativamente alta, y en general, un poco mayor que para λ = 177, para todos los componentes, excepto para la inversión en estructuras y las tres variables gubernamentales. En ambos casos, los valores más bajos de la medida de estabilidad corresponden a estas variables, siendo muy cercanas a la unidad en los otros casos. Las correlaciones cruzadas con el PIB del periodo pasado muestran su menor valor para las variables del sector gubernamental, sin llegar a ser negativas. Las correlaciones más altas con el PIB del siguiente periodo son las de las variables de consumo e inversión. Éstas, asimismo, son características de lo que ocurre con λ= 3016, salvo que la inversión en estructuras también presenta una R² relativamente alta en este caso.

El cuadro 3 muestra las desviaciones estándar de cada uno de los componentes de la demanda agregada como proporción de la desviación estándar del producto nacional bruto (PNB), ordenadas de forma ascendente, de acuerdo con el ordenamiento para λ= 177. Con proporción menor a 1 aparecen el consumo de servicios, el de bienes no durables y el gasto del gobierno estatal. La proporción para el consumo total es mayor a 1 sólo con λ = 177, debido al consumo de bienes durables, que presenta un cociente de 3.28. Para λ = 1600 y λ= 3016, las variables de consumo tienen menor variabilidad como proporción de la del PIB, mientras que la inversión y sus componentes se encuentran en la situación opuesta. La figura 7 presenta gráficamente los datos del cuadro 3, de manera que a simple vista se puede apreciar el orden que mantienen las proporciones de desviación estándar.

El cuadro 4 muestra la correlación de cada componente de la demanda agregada con el PIB del mismo periodo, anterior y siguiente; están ordenados de manera ascendente según la correlación de la variable con el PIB del mismo periodo. En los tres casos, los componentes con menor correlación son las variables gubernamentales; para el caso del gobierno federal y el agregado del gobierno, la correlación con el PIB del periodo pasado supera la que existe con el del mismo periodo.

Es interesante notar que para λ = 177, la desviación estándar de todas las series decrece entre la primera y la segunda mitad, mientras que el comportamiento es opuesto para las series de consumo de servicios e inversión en estructura para λ = 1600 y λ = 3016.

Resulta curioso encontrar algunos cambios de signo en las correlaciones con el PIB y las variables gubernamentales, mientras que con suavidad de 90% el gasto de los gobiernos estatales y locales tiene una correlación levemente negativa con el PIB, como sucede en Hodrick y Prescott (1997), esto no se da con porcentajes de suavidad mayores. Asimismo, se modifica el sentido de la correlación entre el gasto agregado del gobierno y el PIB para la segunda mitad de la serie, conforme aumenta la suavidad de la tendencia. Los resultados presentados también difieren en su conjunto de los de Hodrick y Prescott, ya que en estos últimos la correlación entre el gasto del gobierno federal y el producto en la segunda mitad de la serie (que en su caso cubre datos de 1964 a 1974) es positiva, mientras que en este análisis resultó negativa, sin importar el valor de λ que se elija.

También, es claro que conforme aumenta el valor de λ, aumenta la desviación estándar del componente cíclico, es decir, la desviación estándar de la serie, por ejemplo del PIB. De hecho, se observó que es mayor cuando el filtro HP usa λ = 3016, que cuando se emplea λ = 177. Lo interesante en este caso es que, al dividir la desviación estándar de cada una de las series entre la del PIB, y después ordenarlas de menor a mayor, el orden de las series cambia según el valor de λ, aun cuando en general las series de consumo están por debajo de la unidad (no así en algunos casos la del consumo agregado, que incluye el consumo de bienes duraderos), en tanto que las de inversión se encuentran por arriba de la unidad. Lo mismo pasa si se ordenan de manera ascendente las correlaciones con el PIB, pues el orden se modifica al pasar de λ = 177 a λ = 1600 y se mantiene sin cambios entre λ = 1600 y λ = 3016. Un caso similar es el de las correlaciones con el PIB del periodo anterior y siguiente, para las que difiere el ordenamiento en los tres casos. Por consiguiente, aunque similares, los resultados del análisis para los componentes de la demanda agregada no se mantienen idénticos conforme se modifica el valor de λ, o equivalentemente la suavidad. La elección de porcentajes de suavidad, aun en niveles relativamente cercanos (entre 90 y 95%) puede producir resultados diferentes tanto en las correlaciones como en las desviaciones estándar.

5. Conclusiones

El principal argumento para elegir de antemano un porcentaje de suavidad deseado para la tendencia radica en la comparabilidad de resultados, de manera similar a lo que sucede con las técnicas estadísticas para la estimación de parámetros, en las que se fija el nivel de confianza de los intervalos para poder realizar comparaciones válidas.

La dificultad fundamental que trae consigo la fijación de un determinado nivel de suavidad radica en que no se tiene una idea clara de cuánta suavidad es deseable para un problema específico. Lo que podría hacerse en la práctica es decidir por ensayo y error, después de ver los resultados que produce un cierto nivel de suavidad, en términos del uso que se pretende dar a la tendencia; por ejemplo, al final de la sección 2 se concluyó que la tendencia con mayor suavidad reaccionará con lentitud ante movimientos inesperados de la serie observada (en particular al final de la muestra), por ello, una actitud conservadora para examinar la tendencia de las observaciones más recientes conduciría a preferir los porcentajes de suavidad altos.

Desde luego, la estimación de tendencias puede ser útil simplemente para describir el comportamiento genérico de una serie, así como se usan las medidas de tendencia central para describir conjuntos de datos. La diferencia es que, en este caso, la tendencia central que se describiría tendría un comportamiento dinámico. La inspección visual de los resultados que brinde un cierto porcentaje de suavidad ayudaría, en tal caso, a decidir el porcentaje más apropiado en términos de la apariencia que tenga la tendencia. Si se decidiera aplicar el método de manera rutinaria y masiva, sería importante realizar un estudio piloto para observar el tipo de resultados que se obtienen y elegir, con base en la opinión de expertos, el porcentaje de suavidad más adecuado para un cierto grupo de series. Para realizar otro tipo de estudios, como serían los análisis de ciclos económicos, se requeriría una inspección más detallada de los resultados que se obtienen con diferentes porcentajes de suavidad, pero el criterio del analista es el que, nuevamente, juega el papel más importante en la decisión.

El método que se sugiere aplicar para estimar la tendencia con un porcentaje de suavidad fijado de antemano tiene como ventajas principales que: a) permite comparar tendencias de dos o más series, sin importar que éstas tengan o no el mismo número de observaciones, además de que la comparación puede ser con datos de la misma serie, pero observada en distintos periodos; b) la tendencia también es comparable para series con distintas frecuencias de observación, si se tiene cuidado de elegir la constante de suavizamiento equivalente en forma apropiada y c) se obtienen resultados sustentados en técnicas y modelos estadísticos conocidos, y de relativamente fácil manejo e interpretación.

En el análisis de ciclos que se presentó aquí, queda claro que las series de ciclo que se obtienen están en función del porcentaje de suavidad asignado a la serie de tendencia, y una diferencia mínima en suavidad podría afectar tanto la duración como la intensidad de los ciclos. Estas divergencias pueden conducir a distintas conclusiones sobre los componentes, como sucedió en el estudio de las correlaciones que se mostró aquí. De hecho, pudo observarse que la elección del parámetro λ no es intrascendente. Por tal motivo, debe subrayarse la importancia de informar con base en qué principios se eligió el parámetro al reportar los resultados y las conclusiones de un trabajo que haya empleado el filtro HP.

El énfasis en este trabajo se puso en una selección consciente de un porcentaje de suavidad deseado para la serie de tendencia, así que éste debe ser mencionado explícitamente cuando se reporten los resultados y conclusiones obtenidos para los componentes cíclicos resultantes. De manera adicional, una ayuda fundamental para decidir el porcentaje de suavidad de la tendencia, dentro del contexto del análisis de ciclos, debería ser el ensayo y error o, equivalentemente, la verificación de la sensibilidad de los resultados ante la elección de diferentes porcentajes de suavidad.

Referencias

Berman, J. y J. Pfleeger (1997). “Which industries are sensitive to business cycles?” Monthly Labor Review, 120, 19-26.

Burns, A. F. y W. C. Mitchell (1946). Measuring business cycles. New York, NBER.

Cogley, T. y J. M. Nason (1995). “Effects of the Hodrick–Prescott filter on trend and difference stationary time series. Implications for business cycle research”. Journal of Economics and Dynamic Control. 19, 253–278.

Colín, P. J. U. (2008). Aplicación del filtro de Hodrick-Prescott, con suavidad controlada, para el estudio de hechos estilizados de la economía mexicana. Tesis de Licenciatura en Economía, México, ITAM.

Findley, D. F., B. C. Monsell, W. R. Bell, M. C. Otto y B. C. Chen (1998). “New Capabilities and Methods of the X-12-ARIMA Seasonal-adjustment Program”. Journal of Business and Economic Statistics. 16, 127-152.

Guerrero, V. M. (2005). “Estimating trends with percentage of smoothness chosen by the user”. Documento de trabajo DE-C05.5. Departamento de Estadística-ITAM.

______ (2007). “Time series smoothing by penalized least squares”. Statistics & Probability Letters. 77, 1225-1234.

______ (2008). “Estimating trends with percentage of smoothness chosen by the user”. International Statistical Review. 76, 187-202.

______ (2009). Análisis estadístico y pronóstico de series de tiempo económicas. 3ª edición, México, Just in Time.

Hodrick, R. J. y E. C. Prescott (1997). “Postwar U.S. business cycles: An empirical investigation”. Journal of Money, Credit and Banking. 29, 1-16.

Kaiser, R. y A. Maravall (2001). “Measuring Business Cycles in Economic Time Series”. Lecture Notes in Statistics. 154. New York, Springer,Verlag.

Maddala, G. S. y I. M. Kim (1998). Unit Roots, Cointegration, and Structural Change. Cambridge, Cambridge University Press.

Maravall, A. y A. del Río (2001). “Time aggregation and the Hodrick-Prescott filter”. Documento de Trabajo. Núm. 0108. Servicio de Estudios, Banco de España.

_____ (2007). “Temporal aggregation, systematic sampling, and the Hodrick-Prescott filter”. Computational Statistics and Data Analysis. 52, 975–998.

Nelson, C. R. y C. I. Plosser (1982). “Trends and random walks in macroeconomic time series: Some evidence and implications”. Journal of Monetary Economics. 10, 139-162.

Park, G. (1996). “The role of detrending methods in a model of real business cycles”. Journal of Macroeconomics. 18, 479-501.

Pedersen, T. M. (2001). “The Hodrick–Prescott filter, the Slutzky effect, and the distortionary effect of filters”. Journal of Economics and Dynamic Control. 25, 1081-1101.

Prescott, E. C. (1986). “Theory ahead of business cycle measurement”. Carnegie-Rochester Conference Series on Public Policy. 25, 11-44.

Ravn, M. O. y H. Uhlig (2002). “On adjusting the Hodrick–Prescott filter for the frequency of observations”. Review of Economics and Statistics. 84, 371-376.

Stock, J. H. y M. W. Watson (1999). “Business cycle fluctuations in US macroeconomic time series”. Taylor, J. B. y M. Woodford (eds.). Handbook of Macroeconomics. Vol. I, 3-64. Amsterdam, Elsevier.