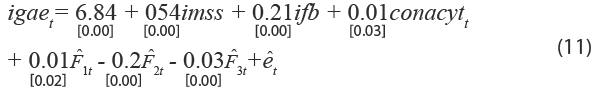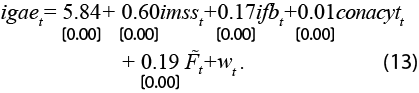Contribución del sistema financiero al crecimiento económico de México: un análisis econométrico, 1997-2019

 

Contribution of the Financial System to Mexico’s Economic Growth:
An Econometric Assessment, 1997-2019

 

 Mauricio Montiel,* Francisco de Jesús Corona Villavicencio** y Jesús López Pérez**
* El Colegio de la Frontera Norte, mmontiel.mea2018@colef.mx
** Instituto Nacional de Estadística y Geografía (INEGI), franciscoj.corona@inegi.org.mx y jesus.lopezp@inegi.org.mx, respectivamente.

 

Vol. 13, Núm. 2 de 2022  Epub                          Contribución del sistema financiero… Epub

Este trabajo contribuye a la discusión sobre si el sistema financiero tiene efectos positivos en el crecimiento económico, separando sus efectos de corto y largo plazo. Utilizando información para el periodo 1997-2019, se analiza la relación entre el Indicador Global de la Actividad Económica, como proxy del Producto Interno Bruto mensual, con los factores de producción, capital y trabajo, la inversión en capital humano y un factor para medir el desarrollo del sistema financiero. Este último se construye a través de modelos de factores dinámicos para incorporar diversas variables relacionadas con el desarrollo del sistema financiero. Enseguida, mediante la descomposición PT de Gonzalo y Granger (1995), se identifica que, ante un choque de corto plazo en el mercado financiero, la actividad económica reacciona positivamente, mientras que un sistema financiero sano contribuye también de manera significativa a la actividad económica en el largo plazo.           Palabras clave: actividad económica; Cobb-Douglas; corto plazo; descomposición PT; modelos de factores dinámicos.

This paper contributes to the academic discussion about whether finance has positive effects on economic growth, separating its short and long-term effects. By using information for the period 1997-2019, we analyze the relation between Indicador Global de la Actividad Económica (IGAE), as a proxy of monthly GDP, with the production factors, capital and labor force, investment on human capital, and a factor that reflect the finance development. The latter is built upon dynamic factor models to incorporate several variables related to the financial system. Next, by using Gonzalo and Granger’s (1995) PT decomposition, we identify that in the face of a short-term shock in the financial market, economic activity reacts positively, whilst a healthy financial system also contributes significantly to economic activity in the long term.                                   Key words: economic activity; Cobb-Douglas; Short-Run; PT decomposition; Dynamic Factor Models.

 

Recibido: 29 de junio de 2020
Aceptado: 19 de octubre de 2021

 

1. Introducción

El sistema financiero ha cobrado relevancia en el desarrollo contemporáneo de la economía mexicana. A partir de la reprivatización de la banca comercial en 1990, y posterior a la crisis de 1994, este se ha conformado acorde con las características y evolución del sector real de la economía, el cual ofrece una diversidad de productos financieros para inversionistas, ahorradores, empresas y emprendedores cada vez más amplia y sofisticada. Por ejemplo, durante la década del 2000 tuvo un gran auge la bursatilización de activos, principalmente hipotecas, que permitieron a los otorgantes de crédito ceder parte del riesgo crediticio. En fecha más reciente, la Ley para Regular las Instituciones de Tecnología Financiera (Fintech), decretada en el 2018, puso a México a la vanguardia en la regulación de empresas que, cada vez más rápido, han adoptado las tecnologías de la información para ofrecer productos y servicios financieros.

Por su parte, la más reciente Encuesta Nacional de Inclusión Financiera^[1] señala que 68 % de la población cuenta con al menos un producto financiero. Aun en el contexto actual de la pandemia ocasionada por el COVID-19, el Banco de México (BANXICO) señala en su Reporte de estabilidad financiera (junio del 2021) que el sistema financiero mexicano ha mostrado resiliencia y una posición en general sólida, caracterizada por niveles de capital y liquidez por encima de los mínimos regulatorios aplicables.

No obstante, existe en la literatura en la materia un debate importante sobre el papel que puede tener el sistema financiero sobre el crecimiento económico de los países.^[2] La discusión clásica versa en dos líneas, por un lado, autores como Lucas (1988) y Robinson (1952) argumentan que la importancia del primero en el segundo se encuentra severamente exagerada en la discusión académica; por otra parte, Schumpeter (1912), Gurley y Shaw (1955), Goldsmith (1969) y Miller (1998) concuerdan que para comprender el crecimiento económico es indispensable tomar en cuenta al sistema financiero.

El principal esfuerzo en probar las teorías antes mencionadas radica en identificar las variables apropiadas para incluirlas en un modelo de regresión lineal. Durlauf (2005) hizo una revisión de distintos estudios y encontró hasta 145 diferentes regresores, en los que la gran mayoría de las variables se han encontrado significativas, los cuales se agrupan en 43 teorías de crecimiento.

Para el caso de México, diversas investigaciones empíricas reconocen la importancia del desarrollo del sistema financiero para el crecimiento económico. Lustig (2001) y Moreno-Brid et al. (2005) coinciden al señalar que las problemáticas del primero generan barreras significativas al segundo. Bergoeing et al. (2002, 2007) identificaron que la colocación ineficiente del crédito durante el periodo 1982-1991 fue un factor importante del pobre desempeño económico en el país, mientras que Venegas et al. (2009) indican que el sistema financiero ejerce una influencia positiva, aunque pequeña,^[3] sobre el crecimiento económico, y para ello evaluaron empíricamente el efecto de uno sobre el otro utilizando metodologías de series de tiempo para conocer los efectos de corto y largo plazo. Cermeño et al. (2012) hicieron un análisis para México y Estados Unidos de América (EE. UU.), donde encontraron que, para el caso de EE. UU., el sistema financiero promueve la tasa de crecimiento económico, pero para nuestra nación hallaron que la relación era inversa. En ese mismo sentido, Méndez-Heras et al. (2021) utilizaron un modelo de mínimos cuadrados ordinarios en dos etapas con datos de panel y uno dinámico de panel, y detectaron que había una relación positiva, estadísticamente significativa, entre el crédito de bancos comerciales y un Índice de Desarrollo Humano estatal elaborado por los autores.

En este orden de ideas, el principal objetivo de este trabajo es analizar de manera empírica la contribución que ha tenido el sistema financiero sobre el crecimiento económico en México. Para ello, utilizamos métodos de series de tiempo para relacionar el Indicador Global de la Actividad Económica (IGAE), como proxy del Producto Interno Bruto (PIB) mensual, con los factores de producción, capital y trabajo, con una variable para medir la inversión en capital humano y con otra para estimar el desarrollo del sistema financiero; el modelo permite separar los efectos de corto y largo plazo de las variables consideradas.

La presente investigación se distingue en introducir al modelo de crecimiento económico un amplio conjunto de variables relacionadas con el desarrollo del sistema financiero, propuestas originalmente por Svirydzenka (2016). En estudios empíricos, el grado de desarrollo del sistema financiero se ha incorporado en un modelo lineal de regresión probando una amplia variedad de variables relacionadas, como: indicadores del mercado de valores, participación de los bancos, dolarización, profundidad del sector bancario, competencia económica, represión financiera, sofisticación de productos bancarios, acceso al crédito, entre otros.

De esta forma, las aportaciones de este trabajo con respecto a la literatura existente son: i) aprovechar al máximo la información de un conjunto de series de tiempo financieras estimando variables latentes con periodicidad mensual de 1997 al 2019, con lo que se reduce la dimensionalidad a través de un modelo de factores dinámico (DFM, por sus siglas en inglés); ii) estimar las posibles relaciones de largo plazo que comparte la actividad económica mensual con el factor trabajo, capital físico acumulado, capital humano y el sector financiero usando, junto con los factores estimados, la prueba de cointegración de Johansen (1991); y sujeto a estos resultados, iii) desentrañar los efectos de corto plazo a través del enfoque de Gonzalo y Granger (1995).

En particular, entender la relevancia del sistema financiero en México es importante, sobre todo en el contexto actual de recuperación económica postpandemia, toda vez que clarificar el entendimiento del rol de este en el crecimiento económico tendrá implicaciones de políticas públicas y creará investigaciones orientadas a la generación de aquellas apropiadas al ámbito nacional.

Lo que resta de este trabajo se distribuye como sigue: en la sección 2 se describe el marco teórico que sustenta las bases de esta investigación; en la 3 se expone la notación y la metodología econométrica; en la 4 se muestra la aplicación empírica y se describen los resultados; y, finalmente, en la 5 se presentan conclusiones.

2. Marco teórico

2.1.Relaciones teóricas entre el sistema financiero y el crecimiento económico

Los paradigmas de crecimiento económico suelen mencionar que este se encuentra supeditado al nivel de inversión en la economía, por ejemplo, y de acuerdo con el modelo neoclásico y a la teoría del modelo AK,^[4] depende en específico de los niveles que se destinen en capitales físico y humano. Por otra parte, según el modelo schumpeteriano de innovación, lo que importa es la que se haga en tecnología y más específicamente, en el grado de inversión en investigación y desarrollo (I + D). Hasta este punto, tales enfoques de crecimiento no reparan en analizar las dificultades que las empresas pueden tener para financiar sus inversiones que lo impulsan, y la función de los bancos y otros intermediarios financieros para hacer frente a dichas restricciones.

De este modo, para comprender el rol que juegan los mercados e intermediarios financieros, es necesario relajar los supuestos de modelos idealizados de crecimiento económico. Ciertamente, el sector financiero es considerado como el lubricante que reduce las fricciones en el sistema económico y, por lo tanto, permite que la maquinaria funcione. Así, las principales funciones de los bancos son: i) distribución de riesgos, ii) promover el ahorro y iii) aliviar problemas de agencia. Aghion y Howitt (2008) introducen restricciones financieras a la teoría schumpeteriana, lo que les permite mostrar cómo los intermediarios financieros, al canalizar el ahorro, proveen financiamiento externo a los emprendedores que innovan y eso, a su vez, promueve el crecimiento económico.

2.2. Relaciones empíricas entre el sistema financiero y el crecimiento económico

La mayoría de la literatura en esta materia se relaciona con regresiones tipo panel entre países de la forma:

g_i = β₀ + β₁ DesFin_i + β₂X_i + u_i

donde g_i es el promedio de crecimiento del país i durante el periodo de análisis, DesFin_i es el nivel de desarrollo financiero del país, X_i es un vector de variables control y u_i es un término de error. Los diferentes estudios difieren en: i) cómo tomar la variable de crecimiento de la economía, ya sea utilizar datos para diferentes países o bien para distintas industrias y regiones, o bien empleando datos a nivel de empresa; o ii) la forma en la que se mide DesFin_i.

Entre las referencias más importantes se encuentra Goldsmith (1969), quien trató de evaluar si el sistema financiero ejerce una influencia en el crecimiento económico mostrando que existe una correlación positiva entre el tamaño del primero y el nivel de actividad económica. Por su parte, McKinnon (1973) interpretó la gran cantidad de evidencia que emerge de estudios de caso de países y sugirió que los sistemas financieros que funcionan mejor han estimulado de manera importante el crecimiento económico. King y Levine (1993) se basaron en el trabajo de Goldsmith (1969) y estudiaron un total de 77 naciones con el objetivo de determinar si el sistema financiero contribuye al crecimiento económico de largo plazo, a la acumulación de capital y a la productividad; estos autores concluyen que hay una fuerte relación entre el primero y el segundo.^[5]

El grueso de evidencia empírica indica que el desarrollo financiero afecta al crecimiento económico de una forma positiva y monotónica, ya que los países con bancos y mercados más eficientes crecen más rápido, y cuando los sistemas financieros funcionan mejor alivian las restricciones de financiamiento externo que impiden la expansión industrial y de las empresas, mientras que los bancos proveen servicios de búsqueda de proyectos de inversión (screening services) y realizan monitoreo postpréstamo (Levine, 2005).

La evidencia más reciente ha sugerido que este no es necesariamente el caso de todos los tipos de actividad y en la totalidad de los niveles de desarrollo financiero (Popov, 2018). Por ejemplo, en un trabajo reciente, Ruiz (2018) utilizó una estimación de variables instrumentales y modelos de panel para controlar por endogeneidad al trabajar con el PIB per cápita inicial, y encontró evidencia que corrobora la existencia de una relación no lineal entre el desarrollo financiero y el crecimiento económico. Slesman et al. (2019) hallaron, en un estudio de 77 países emergentes y en vías de desarrollo, que al minimizar los riesgos políticos a través de mejoras en la calidad de las instituciones políticas es posible mejorar el crecimiento económico debido al desarrollo del sistema financiero. Maune et al. (2020) utilizaron un modelo de regresión múltiple para evaluar el impacto de la inclusión financiera en Zimbabue en el periodo del 2011 al 2017, y encontraron que la inclusión financiera tenía un impacto positivo en el crecimiento del país.

En el polo opuesto, hay quienes argumentan que en la práctica existen ciertas desventajas del desarrollo financiero. A través de la historia, las finanzas han sido señaladas como una actividad de búsqueda de rentas (rent seeking^[6]). En consecuencia, terminan por aumentar la fragilidad de las instituciones financieras, la inestabilidad macroeconómica y la probabilidad de crisis financieras, por lo que se exacerba la caída de la tasa de crecimiento económico de largo plazo (Venegas et al., 2009). Ibrahim y Alagidede (2018), en un panel de 29 países subsaharianos para el periodo 1980-2014, utilizando la técnica de estimación dinámica mediante el método generalizado de momentos (GMM, por sus siglas en inglés), encontraron que mientras el desarrollo financiero apoya al crecimiento económico, el grado en el que las finanzas lo ayudan depende de manera crítica del crecimiento simultáneo de los sectores real y financiero. Kadhuma y Kadhimb (2020) analizaron los efectos de la represión financiera en el crecimiento económico en Irak; sus resultados muestran que la liberalización financiera y de capitales tienen un efecto negativo y no significativo. Más recientemente, Cheng et al. (2021) usaron un panel de 72 naciones para el periodo 2000-2015 y, empleando GMM, hallaron que, sin importar el nivel de ingreso del país, el desarrollo financiero es siempre desfavorable para el crecimiento económico, pero este efecto es mayor en países de ingresos altos.

Una parte importante de la literatura investiga la relación entre finanzas y crecimiento económico utilizando métodos de series de tiempo. Este enfoque permite emplear técnicas econométricas más poderosas para analizar naciones en particular a mayor profundidad (Levine, 2005). Estas investigaciones con frecuencia hacen uso de pruebas de causalidad de Granger, como lo realizan Blomstrom et al. (1996) para explicar el crecimiento económico con la formación de capital empleando rezagos de ambas series; de manera similar, Campos y Nugent (2002) investigaron la existencia y dirección de una relación causal entre inestabilidad sociopolítica y el crecimiento económico. Otro procedimiento utilizado ampliamente en la literatura es el de vectores autorregresivos (VAR), como en Dritsakis y Adamopoulos (2004), quienes analizaron el PIB trimestral en función de agregados monetarios y la apertura comercial.

Los modelos de series de tiempo también se han utilizado en la literatura de crecimiento endógeno para analizar cambios permanentes en variables que son afectadas potencialmente por políticas gubernamentales, las cuales conllevan a modificaciones permanentes en la tasa de crecimiento económico, tal es el caso de Jones (2005), quien evaluó modelos de crecimiento AK y de I + D, en los que modeló de manera explícita la inversión y el cambio tecnológico, y encontró que un incremento permanente en la tasa de crecimiento de la inversión afecta al crecimiento económico solamente en un corto periodo de ocho años.

Destacan, además, las restricciones gubernamentales que se han dado sobre el sistema financiero, como los límites establecidos sobre las tasas de interés, el encaje legal, entre otras, las cuales han distorsionado el proceso de desarrollo de este. De acuerdo con Rodríguez y López (2010), este efecto podría deberse a las imperfecciones que provocan tales restricciones en los mercados financieros, produciendo una asignación ineficiente de recursos.

De esta forma, en este trabajo nos centramos en cuantificar variables latentes financieras que puedan ser relacionadas con el crecimiento económico.

3. Metodología econométrica

En esta sección se describe esta y la notación empleada a lo largo de la investigación.

3.1. Modelos de factores dinámicos

En economía, estos fueron originalmente introducidos por Geweke (1977) y Sargent y Sims (1977) y son utilizados con frecuencia para representar la dinámica de un grupo de N series de tiempo correlacionadas a través de un pequeño número de factores comunes subyacentes (r<N). En la actualidad, dada la vasta cantidad de información recopilada a través de las décadas pasadas, el uso de los DFM de alta dimensionalidad se ha vuelto más atractivo debido a la flexibilidad que brinda el poder extraer en pocos factores la variabilidad asociada a un gran número de variables.

En este contexto, consideramos que la evolución común de un vector de series de tiempo que representan al mercado financiero,  X_t = (x_1t, … x_Nt )‘, observadas desde t = 1, … , T, son generadas por factores comunes no observados  F_t = (F_1t, … , F_rt)‘ más ruidos idiosincráticos o comportamientos individuales, ε_t = (ε_1t, … , ε_Nt)‘, donde estos dos últimos siguen su propia dinámica; en este caso, se asume como un modelo tipo VAR(1). En consecuencia, el DFM está representado como sigue:

X_t = PF_t + ε_t,

F_t = ΦF_t-1 + η_t,

                                   ε_t=Γε_t-1 + a_t,                           (4)   

donde X_t, ε_t y a_t  = (a_1t, … ,a_Nt)‘ son vectores de dimensión N × 1. La contribución de los factores sobre las observaciones está dada por la matriz de cargas, P = (p₁, … ,p_N)‘, cuya dimensión es N × r, mientras que F_t y su término idiosincrático η_t = (η_1t, … ,η_rt)‘ son vectores de dimensiones r x 1. Se asume que a_t y η_t son ruidos blancos con matrices de covarianzas Σ_a y Σ_n = diag (σ²_n1, … σ²_nr), respectivamente, en tanto que Φ = diag (Φ₁, … Φ_r) y Γ = diag (γ₁, … γ_r) son matrices de dimensión r × r y N × N, las cuales contienen los parámetros autorregresivos de los factores y de los componentes idiosincráticos, en ese mismo orden. Las diagonales principales de Φ pueden contener valores de 1 y, de esta manera, los factores comunes pueden ser no estacionarios. Por otra parte, y por conveniencia, se asume que la diagonal de Γ es tal que los errores idiosincráticos son estacionarios.

El procedimiento más popular para extraer factores en DFM de alta dimensionalidad es el de componentes principales (PC, por sus siglas en inglés) debido a la facilidad para implementarlo computacionalmente y que la teoría asintótica, dado los supuestos de las ecuaciones (4), es bien conocida. Su particularidad principal es que nos permite extraer los factores sin asumir nada en particular sobre la distribución de los errores; además, su implementación es computacionalmente simple, lo cual puede explicar por qué se usa con frecuencia en estudios que enfrentan una numerosa cantidad de variables y observaciones en forma de series de tiempo. La extracción de factores a través de PC separa el componente común, PF_t, del idiosincrático, ε_t, mediante promedios de sección cruzada sobre X_t de tal manera que cuando N y T tienden a infinito, el efecto del componente idiosincrático converge a 0, dejando solo los efectos asociados a los factores comunes; ver, por ejemplo, Corona et al. (2017). Se puede mostrar que la estimación de P obtenida por PC, , es equivalente a √N veces los vectores propios correspondientes a los r valores propios más grandes de X’ X, donde X = (X₁, … ,X_t) es una matriz de dimensión N × T . En consecuencia, la estimación de  F con PC es, entonces:

           

La consistencia de   y dependen de que el componente idiosincrático sea estacionario; por ende, se asume que ε_t ∼ I(0), ver Bai (2003, 2004), no obstante, en la práctica esto tiene que ser verificado (Bai y Ng, 2004).

Hasta este momento hemos asumido que r es conocido, pero en la práctica tiene que estimarse. En Corona et al. (2017) se realizan extensos experimentos Monte Carlo para diagnosticar qué criterio de estimación es el que funciona mejor bajo diferentes procesos generadores de datos, evaluando series de tiempo estacionarias y no estacionarias. En este trabajo se estudian los criterios de Bai y Ng (2002), Onatski (2010) y Ahn y Horenstein (2013), concluyendo que el de Onatski funciona mejor cuando las series de tiempo son incluso no estacionarias y las dependencias en el componente idiosincrático son relativamente fuertes, es decir, hay autocorrelación serial, heteroscedasticidad y correlación contemporánea entre los errores. También, en Corona et al. (2017) se muestran cómo estos criterios dependen de la magnitud de los valores propios de la matriz de covarianza de las observaciones, es decir, λ_j , para j = 1, … , N; en este sentido, en este trabajo nos centramos en el tradicional criterio basado en la explicación de la varianza:

donde c es un número fijo predeterminado, conocido como el porcentaje de la explicación de la varianza, frecuentemente 0.8 o 0.9.

3.2. Relaciones dinámicas de corto y largo plazo: Gonzalo y Granger (1995) y Johansen (1991)

En un correcto orden de ideas, se asume que  es un vector (4 × r) × 1, donde y_t es el nivel de actividad económica; l_t es atribuible al factor trabajo y k_t, a la acumulación de capital físico; h_t mide al capital humano; y F_t son las variables latentes atribuibles al sistema financiero. Asumiendo que Y_t ∼ I(1), el vector de corrección de errores (VEC) es:

                               
ΔY_t = ΠY_t-p + Γ₁ ΔY_t-1 + Γ₂ ΔY_t-2 + ⋯ + Γ_p-1 ΔY_t-p+1 + u_t,                       (7)

donde se supone que u_t es ruido blanco. La prueba de cointegración de Johansen (1991) es ampliamente conocida en la literatura, y, en resumen, se orienta en las raíces características de la matriz  Π = αβ’ del modelo (7). En pocas palabras, el rango de Π especificará el número de vectores de cointegración que estén presentes en el sistema, es decir, el número de relaciones de largo plazo. Si rango (Π) = 0, todos los elementos de Π son 0 y (7) puede reescribirse como un modelo VAR(p) en primeras diferencias. En este caso, Y_y tiene raíz unitaria y ninguna de las variables está cointegrada. Si, por el contrario, rango (Π) = 4 × r, el vector Y_t es estacionario e igualmente no cointegrado, es decir, el modelo (7) es un VAR(p). En los casos intermedios donde 1 < rango(Π) < 4 × r, quiere decir que existen múltiples vectores de cointegración y, si suponemos que rango (Π) = m, tal que el número de vectores de cointegración independientes sea m, entonces solo esas m relaciones lineales de las variables conducirán a un resultado estacionario. En otras palabras, hay  m vectores de cointegración, siendo estas β’Y_t.

En este último caso, Stock y Watson (1988) muestran que series de tiempo cointegradas permiten una representación de factores similar de la siguiente manera:

donde la dimensión de f_t es k=N-m y . En palabras, Z_t ∼I(1) son las tendencias comunes de Y_t. Gonzalo y Granger (1995) otorgan las condiciones para estimar f_t; primero establecen que f_{t =} BY_t, es decir, es una combinación lineal de las variables originales, de tal forma que A1Z_t puede ser asociado al componente permanente de Y_t y  al transitorio. Esta descomposición es conocida como descomposición PT y, de acuerdo con Blanchard y Quah (1989), es necesario que se cumpla lo siguiente para que esta sea válida:

1. Y_t = P_t + T_t. 
2. ΔP_t y  T_t son estacionarias.
3. Para el modelo H(L)Y_t = u_t:
   1. 
   2. 

Es decir, solo los choques permanentes tienen efecto en el largo plazo en las observaciones, mientras que los transitorios no. De esta manera, sujeto a los resultados de cointegración, la idea intuitiva de Gonzalo y Granger (1995) es que si β’ Y_t~I(0), se puede expresar una descomposición que cumpla con las condiciones anteriores tal que Y_t = A₁f_t + A₂Z_t, donde Z_t = β’ Y_t. Es demostrable que dicha combinación es, finalmente:

                                Y_t = A₁f_t + A₂Z_t = P_t + T_t,                                  (9)

donde A₁ = β_⊥ (α‘_⊥β_⊥)^-1, f_t = α’_⊥ Y_t  y  A₂= α(β’α)^-1. Gonzalo y Granger (1995) dan las pautas para estimar A₁ y A₂, que se basa en estimar el complemento ortogonal, α_⊥, lo cual es basado en máxima verosimilitud usando un procedimiento similar al proceso de estimación de α y β en Johansen (1991). En este trabajo, por interpretabilidad, para analizar el corto plazo nos centraremos en A₂, que contiene los efectos de los choques transitorios, mientras que, para el largo plazo, nos enfocaremos en las tradicionales ecuaciones de cointegración, es decir, β’ Y_t. Nótese que, en consecuencia, A₁ es la contribución de las tendencias comunes sobre las observaciones.

4. Aplicación empírica

En esta sección detallamos los datos utilizados en este trabajo y los resultados de aplicar la metodología descrita en el apartado anterior.

4.1. Datos

Las fuentes de información empleadas en este trabajo tienen periodicidad mensual, desde julio de 1997 hasta octubre del 2019. Estas se describen a continuación:

• Series financieras:
  • Cartera vigente (cv): como proporción del PIB (fuente: BANXICO e INEGI).
  • CETES a 28 días (cetes28): en términos reales, utilizando la inflación calculada con el Índice Nacional de Precios al Consumidor (INPC) base 2013 = 100 (fuente: BANXICO e INEGI).
  • CETES a 91 días (cetes91): en término reales deflactado con el INPC base 2013 = 100 (fuente: BANXICO).
  • CETES a 128 días (cetes128): en términos reales deflactado con el INPC base 2013 = 100 (fuente: BANXICO).
  • CETES a 364 días (cetes364): en términos reales deflactado con el INPC base 2013 = 100 (fuente: BANXICO).
  • Índice de Precios y Cotizaciones de la Bolsa Mexicana de Valores (ipcg): indicador del mercado accionario en su conjunto (fuente: BANXICO).
  • Índice del Tipo de Cambio Real (itcr): con respecto a 49 países (fuente: BANXICO).
  • Agregado monetario M1 (m1): compuesto por instrumentos altamente líquidos en poder de los sectores residentes tenedores de dinero; en particular, incluye billetes y monedas emitidos por el Banco de México, así como depósitos de exigibilidad inmediata en bancos y entidades de ahorro y crédito popular; serie deflactada con el INPC base 2013 = 100, desestacionalizada y como proporción del PIB (fuente: BANXICO e INEGI).
  • Agregado monetario M2 (m2): instrumentos monetarios a plazo en poder de los sectores residentes tenedores de dinero; en particular, incluye la captación con un plazo residual de hasta cinco años en bancos, entidades de ahorro y crédito popular, así como uniones de crédito, las acciones de los fondos de inversión de deuda y los acreedores por reporto de valores; serie deflactada con el INPC base 2013 = 100, desestacionalizada y como proporción del PIB (fuente: BANXICO).
  • Agregado monetario M3 (m3): valores públicos en poder de los sectores residentes tenedores de dinero y que fueron emitidos por el Gobierno Federal, BANXICO (BREMS) y el Instituto para la Protección al Ahorro Bancario (IPAB); serie deflactada con el INPC base 2013 = 100, desestacionalizada y como proporción del PIB (fuente: BANXICO).
  • Agregado monetario M4 (m4): tenencia por parte de no residentes de todos los instrumentos incluidos en M3; serie deflactada con el INPC base 2013 = 100, desestacionalizada y como proporción del PIB (fuente: BANXICO).
• Series económicas:
  • PIB mensual (igae): PIB real mensualizado a través de la técnica de Denton-Cholette (Denton, 1971) utilizando como variable preliminar al IGAE; serie desestacionalizada (fuente: INEGI).
  • Asegurados permanentes y eventuales del IMSS (imss): número de trabajadores asegurados, permanentes y eventuales inscritos en el Seguro Social; serie desestacionalizada (fuente: IMSS).
  • Inversión fija bruta, Índice de Volumen Físico Acumulado (ifb): total, incluye construcción y maquinaria y equipo, base 2013 = 100; se desestacionaliza (fuente: INEGI).
  • Presupuesto asignado al Consejo Nacional de Ciencia y Tecnología (conacyt): serie desestacionalizada y como proporción del PIB, base 2013 = 100 (fuente: SHCP).

La desestacionalización de las variables no desestacionalizadas previamente se realizó con el paquete estadístico R con ayuda de la librería seasonal, que incluye los métodos del paquete X13-ARIMA-SEATS.

Finalmente, las series se expresan en logaritmos naturales por dos motivos: i) para eliminar la posible dependencia multiplicativa en la varianza de las series y ii) para realizar el ejercicio de cointegración donde los coeficientes representen las elasticidades.

Se realizaron pruebas Dickey-Fuller aumentadas (ADF, por sus siglas en inglés), donde se concluye que todas las series de tiempo son I(1).

4.2. Obteniendo indicadores financieros

El primer paso consiste en estimar factores subyacentes del grupo de variables financieras a través de DFM de alta dimensionalidad usando los métodos descritos en la subsección 3.1. Para lo anterior, un primer paso descriptivo consiste en analizar la estructura de correlación entre las series de tiempo. Es claro que, mientras más correlacionadas estén las variables, más sentido tendrá aplicar la reducción de la dimensionalidad. En este caso, la dependencia efectiva muestral^[7] es de 0.960, por lo cual existe una clara dependencia lineal multivariada.

Estimando la expresión (6) nos otorga un  , lo cual nos dictamina que, de las 12 series de tiempo financieras, tres variables latentes explican al menos 90 % de la variabilidad total observada. La estimación de la matriz  se puede observar en el cuadro 1.

Claramente, el primer factor es dominado negativamente por las tasas de interés y de manera positiva, por el resto de las variables con excepción del m2, aunque su contribución es menor. El segundo carga positivamente para el resto de las variables, donde sobresalen las contribuciones de m2, itcr y m4. Por último, el tercero es dominado de forma negativa por casi todas las variables financieras. La intuición económica de estos factores es que, si el primero, el cual tiene mayor grado de explicación, carga de manera positiva respecto a la actividad económica, se verá beneficiado cuando las tasas de interés son bajas y el resto de las variables altas. Para el segundo, se podría argumentar lo contrario, que la economía se verá beneficiada por tasas de interés altas, mientras que el tercer factor tiene una interpretación poco más compleja, pero en definitiva indica que la economía se ve beneficiada cuando el tipo de cambio real y las tasas de interés decrecen.

La validación económica de los factores se presenta en la siguiente subsección, no obstante, econométricamente, la estimación de estos es consistente siempre y cuando se pueda corroborar que el componente idiosincrático es estacionario. Para estos fines, se realiza la prueba PANIC de Bai y Ng (2004) dada por el siguiente estadístico:

donde φ_i son los p-valores individuales de las pruebas de raíces unitarias individuales ADF para los elementos contenidos en  . La hipótesis nula indica que hay una raíz unitaria múltiple, es decir, los errores son no estacionarios, mientras que la hipótesis alternativa, lo contrario. De esta manera, se obtiene un Ø = 9.964 que genera un p-valor de 0.00, por lo cual podemos concluir que los errores idiosincráticos son estacionarios y, por ende, los factores estimados son consistentes estadísticamente.

4.2.1. Validación económica

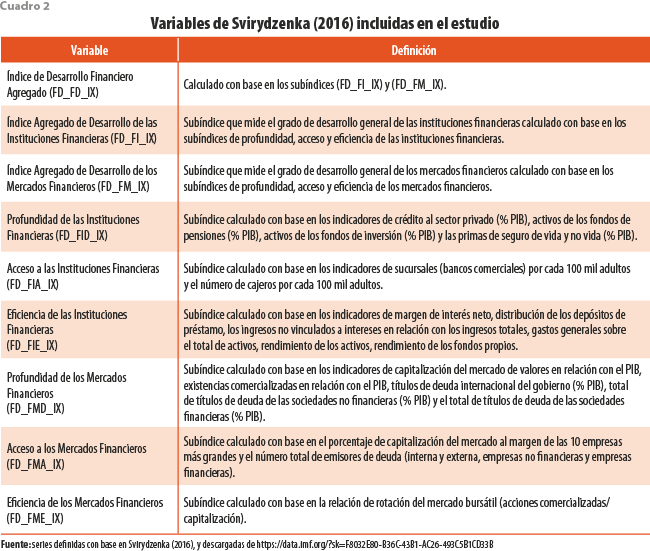
Para validar en un sentido estructural los factores subyacentes estimados, se propone compararlos y analizarlos con indicadores ya publicados por instituciones internacionales y validados de manera empírica, pero con periodicidad mayor (en este caso anual) y su cobertura de tiempo es menor, motivo por el cual no pueden ser directamente utilizados en este trabajo. De esta forma, los tres factores subyacentes son comparados con los indicadores publicados en el Fondo Monetario Internacional (FMI) por Svirydzenka (2016), los cuales se pueden apreciar en el cuadro 2.

Para esta comparación, los factores subyacentes se analizan promediando los valores mensuales para obtener el anual y se comparan con los indicadores propuestos previamente descritos. Las gráficas 1 muestran los comportamientos para el primer factor estimado.

 

Se puede apreciar que el factor común tiene una tendencia positiva durante todo el periodo, cuyas correlaciones son positivas para todos los casos, excepto para FD_FME_IX, donde el valor estimado es de -0.22. Las correlaciones superiores a 0.90 se obtienen con FD_FIA_IX, FD_FID_IX, FD_FD_IX y FD_FI_IX, con valores de 0.97, 0.92, 0.91 y 0.90, respectivamente.

Asimismo, vale la pena comentar que estas altas correlaciones no son espurias bajo la concepción de Engle y Granger (1987), ya que se puede argumentar que las series están cointegradas para estos pares. Para este primer factor y a un nivel de significancia de 10 %, las correlaciones espurias se obtienen para FD_FM_IX, FD_FIE_IX y FD_FMA_IX, aunque los valores son 0.69, 0.46 y 0.35, respectivamente; es decir, en estos casos no se puede establecer estadísticamente que las series están cointegradas. Las gráficas 2 muestran lo mismo que las 1, pero haciendo referencia al segundo factor.

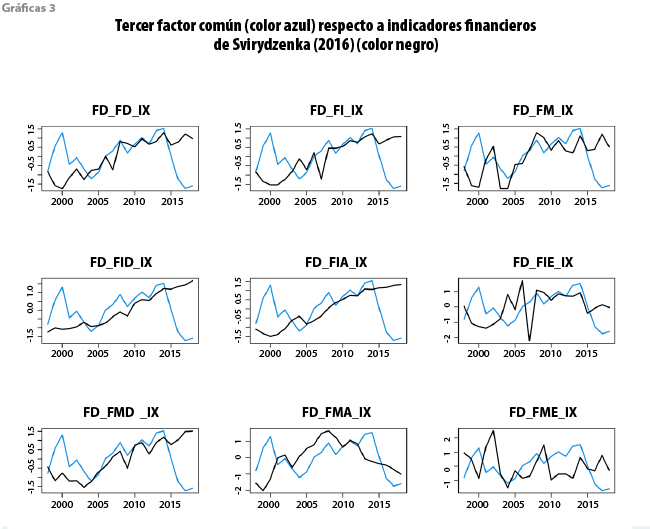
Es posible observar que el segundo factor común tiene una caída fuerte en los primeros periodos y después presenta una tendencia positiva en el resto, cuyas correlaciones son positivas para todos los casos, excepto para FD_FMA_IX, donde el valor estimado es de -0.46. En este caso no existen correlaciones altas, siendo la mayor con FD_FMD_IX con un valor de 0.42. Estas correlaciones, aunque bajas, no son espurias, es decir, para este segundo factor y a un nivel de significancia de 10 %, se puede establecer estadísticamente que todos los pares de series están cointegrados. Finalmente, respecto a este análisis, las gráficas 3 presentan las relaciones del tercer factor respecto a cada una de las series financieras.

En este caso, el tercer factor común no parece presentar ninguna tendencia a largo plazo, mostrando algunas caídas y recuperaciones importantes durante todo el periodo; sin embargo, las correlaciones son positivas para casi todos los casos, excepto para FD_FID_IX, FD_FIA_IX y FD_FME_IX, donde el valor estimado es de -0.036, -0.038 y -0.091, respectivamente. En general, todas las correlaciones positivas están por debajo de 0.30, siendo la más alta la de FD_FID_IX con un valor de 0.27. Aun con estas correlaciones bajas, las relaciones no son espurias, ya que se puede argumentar que las series están cointegradas para estos pares; es decir, para este tercer factor y a un nivel de significancia de 10 %, se puede establecer estadísticamente que todos los pares de series están cointegrados.

4.2.2. Experimento Monte Carlo

Una vez verificada la consistencia estadística de la estimación de los factores a través de la prueba de Bai y Ng (2004) y también en un sentido estructural al correlacionar los factores subyacentes con los indicadores financieros de Svirydzenka (2016), se realiza además un experimento Monte Carlo con el fin de validar en un sentido muestral que las estimaciones de los factores, bajo las condiciones específicas en tamaño de muestra y no estacionariedad de las series utilizadas en este trabajo, se pueden extraer los que serían los verdaderos factores.

La justificación de verificar la consistencia obedece a que, aunque la estimación de los factores por PC genera buenos resultados para tamaños de muestra relativamente pequeños usando diferentes procesos generadores de datos (Corona et al., 2018), las condiciones pueden variar según el conjunto de datos utilizado.

Ante este panorama, se genera un experimento Monte Carlo usando M = 500 réplicas, T = 300, N = 12 y r =3. Los parámetros del DFM son los siguientes:

Asimismo, Σ_α es simulada tal que permite débil correlación cruzada. Nótese que este experimento indica que los factores son no estacionarios, por ende, las series son no estacionarias; el primero es más fuerte que el segundo y este, que el tercero. Finalmente, aunque los errores idiosincráticos son estacionarios, estos tienen alta correlación serial y débil cruzada. En otras palabras, son condiciones similares a las cuales se estimaron los factores financieros.

En cada réplica computamos el promedio de las bondades de ajustes (R²) al realizar las regresiones , es decir, tratamos de explicar la variación en los factores simulados (verdaderos) con los estimados en la sección anterior. Los resultados indican que para los cuantiles 5, 50 y 95 % las R² son 0.94, 0.98 y 0.99, y con ello podemos concluir que al hacer la estimación de los factores a través de PC se obtienen precisiones muy cercanas a lo que serían los verdaderos factores. De esta manera, el experimento Monte Carlo arroja evidencia de que, en muestras finitas, las estimaciones de los factores son confiables y robustas para el número de series consideradas y las dinámicas de cada uno de los componentes del DFM.

4.3 Relaciones dinámicas: corto y largo plazo

Los resultados de cointegración usando la prueba de Johansen (1991), específicamente la del máximo valor propio a 5 % de significancia, nos indican que no rechazamos la hipótesis nula para m≤3, cuyo valor crítico es de 28.14, donde el estadístico de la prueba es de 26.41. De esta manera, existen hasta tres combinaciones lineales de series de tiempo no estacionarias que sí lo son. Centrándonos en la primera ecuación de cointegración normalizada respecto a la actividad económica, la cual es más informativa en sentido estructural, los coeficientes de largo plazo están dados por la siguiente ecuación (valores p entre corchetes):

Esta ecuación tiene varias consideraciones en términos económicos, primero nótese que la suma de los parámetros asociados a los factores trabajo, capital y capital humano es de 0.76, menor a 1; más aún, la suma de todos los coeficientes de la ecuación (11) es de apenas 0.81, lo cual nos puede dar indicios de que las variables proxy de la función Cobb-Douglas no capturan el crecimiento en el largo plazo como función de los factores de la producción y las variables de desarrollo financiero, es decir, nuestro método genera estimaciones sesgadas hacia abajo. Esto puede mostrar indicios de omisión de variables, para lo cual se podrían considerar en particular aquellas que permitan capturar de mejor manera la aportación del capital humano, ya que la contribución de esta variable es muy pequeña. En Durlauf (2005) se sugieren, por ejemplo, nivel de estudios, nivel de estudio en las mujeres, grado de cumplimiento de nivel básico de educación, proporción de estudiantes de ingeniería, entre otras.

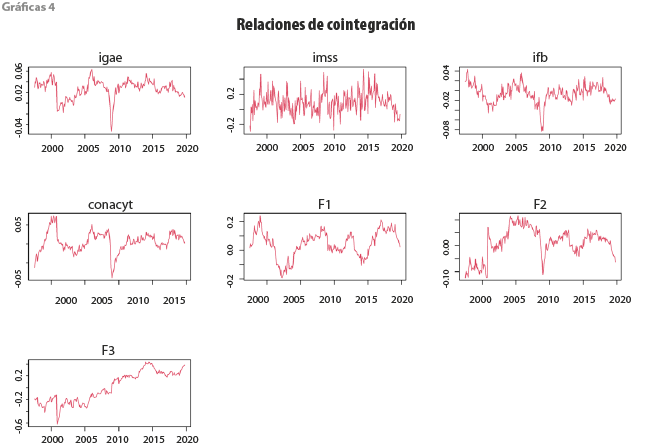
No obstante, con respecto a los factores comunes, nótese que estos no son interpretables como variables en sí, sino como factores subyacentes que son producto de una estimación proveniente de variables observables. En ese sentido, lo más relevante es que todas las series de tiempo son significativas para explicar los niveles de la actividad económica en el largo plazo. En las gráficas 4 se muestra el comportamiento de las relaciones de cointegración normalizando respecto a cada una de las variables.

Es de interés denotar el comportamiento estacionario de cada una de estas, lo que verifica que existen combinaciones lineales de series de tiempo no estacionarias que sí lo son. Nótese que el tercer factor, aunque presenta tendencia, es estacionario una vez eliminado el efecto de una tendencia determinística, obteniendo un valor p en la prueba ADF de 0.02. Enfocándonos en la actividad económica, la relación de cointegración nos indica la desviación que existe respecto a los efectos de largo plazo, llamando la atención la caída de la crisis financiera del 2009.

Para validar estadísticamente el modelo, nos centramos en evaluar los supuestos de no autocorrelación serial en los errores, û_t, en la ecuación (7), para lo cual estimamos pruebas Ljung-Box con hasta siete rezagos, ecuación por ecuación y estimando la mediana de los p-valores para cada una de estas. En este sentido, probamos que ninguna de las ecuaciones tiene problemas de autocorrelación, por lo que puede concluirse que los coeficientes asociados al VEC se estiman de manera eficiente. Otra prueba es la normalidad residual, y aunque algunos residuales no se distribuyen normalmente, como las ecuaciones del ifb y de los factores financieros, nótese que, asintóticamente, podemos relajar este supuesto sin repercusiones en las propiedades de los estimadores asociados al VEC expresado en (7).

Los efectos de corto plazo son estimados a partir de la matriz  de la ecuación (9), es decir, las ponderaciones lineales que no tienen efectos de largo plazo. La estimación normalizada para el igae se expresa como sigue:

En este caso, podemos apreciar que en el largo plazo se mantienen los mismos signos que en el corto, aunque la magnitud asociada a los factores financieros es mayor que las variables consideradas como estructurales, que son los factores clásicos de la producción. Esto debe tomarse con cautela dado que las series que dan forma a estos son estandarizadas, por lo que, como hemos comentado, los coeficientes no deben interpretarse directamente como propensiones o elasticidades, no así el signo, el cual nos indica la contribución de los factores subyacentes, en este caso, las relaciones de cointegración sobre las observaciones.

Una interpretación natural del primer factor común es la siguiente:

1. Largo plazo: cuando las tasas de interés disminuyen (cambio marginal negativo) y el resto de las variables financieras incrementan (positivo), esto beneficia a la actividad económica en el largo plazo de manera significativa, donde sobresale el efecto del Índice de Precios y Cotizaciones, la liquidez y el efecto de la cartera vigente, es decir, un sistema financiero sano.
2. Corto plazo: cuando hay un choque de corto plazo en el mercado financiero, producto de un incremento de la actividad financiera respecto a su comportamiento de largo plazo, la actividad económica reacciona positivamente.

En la siguiente subsección se presenta una discusión detallada de los resultados en términos económicos.

4.4. Discusión de los resultados

Hemos indicado el debate existente acerca del papel que puede tener el sistema financiero sobre el crecimiento, y nuestros resultados coinciden con el pensamiento de diversos economistas teóricos que están de acuerdo en que para comprender el crecimiento económico es indispensable tomar en cuenta al sistema financiero.

Es en ese sentido que esta investigación se orienta en observar el papel que juegan las finanzas en el proceso de crecimiento económico en el corto y largo plazo. Se utilizan variables de frecuencia mensual desde 1997 hasta el 2019, lo que permite realizar un análisis más detallado y robusto en comparación con la literatura previa. En todos los cálculos se verifica la consistencia estadística, económica y empírica. Se determinaron tres variables latentes que representen al sistema financiero mexicano, las cuales son estimadas consistentemente de acuerdo con la prueba PANIC de Bai y Ng (2004). Además, en un sentido estructural, se valida que dichos factores tienen alta relación lineal con indicadores financieros publicados por organismos internacionales que miden la profundidad, el acceso y la eficiencia de este. También, mediante un experimento Monte Carlo, se computa el promedio de las bondades de ajustes entre los factores simulados y los estimados. Los resultados indican que para los cuantiles 5, 50 y 95 % las R² son 0.94, 0.98 y 0.99, es decir, la estimación obtiene precisiones muy cercanas a lo que serían los verdaderos factores y, por lo tanto, estos son muestralmente consistentes.

Los factores estimados se utilizan para realizar pruebas de cointegración en conjunto con variables económicas clave del crecimiento. En este sentido, la prueba de Johansen (1991) indica la existencia de hasta tres vectores de cointegración. Centrándonos en la primera ecuación de cointegración normalizada respecto a la actividad económica, los coeficientes de largo plazo de los factores de trabajo, capital y capital humano (0.54, 0.21, 0.01, respectivamente) son todos positivos, pero suman menos de la unidad al igual que la suma de todos los coeficientes de la ecuación, lo cual nos puede dar indicios de que las variables proxy de la función Cobb-Douglas no capturan en su totalidad la contabilidad del crecimiento económico a través de los factores de la producción. Por otra parte, esto también nos puede indicar que empíricamente existen otras variables que no están siendo consideradas.

Las estimaciones aquí realizadas están basadas en el modelo con restricciones financieras a la teoría de crecimiento schumpeteriana. Uno de los resultados más relevantes es que todas las series son significativas para explicar los niveles de la actividad económica en el largo plazo; además, los signos de los factores de producción y el primer factor financiero son positivos, de acuerdo con lo esperado.

En específico, esto implica que, cuando las tasas de interés reales presentan un cambio marginal negativo y el resto de las variables financieras muestran uno positivo se beneficia a la actividad económica en el largo plazo de manera significativa, donde sobresale el efecto del Índice de Precios y Cotizaciones, la liquidez y el de la cartera vigente. Con respecto al corto plazo, calculado con la metodología Gonzalo y Granger (1995), los coeficientes para trabajo, capital y capital humano son 0.49, 2.48 y 0.51, respectivamente, y con respecto a los tres factores financieros sus coeficientes son 10.35, -1.31 y -7.57, esto quiere decir que cuando hay un choque en el mercado financiero, producto de un incremento de la actividad financiera respecto a su comportamiento de largo plazo, la actividad económica reacciona positivamente. Se debe tener en cuenta que los tres factores comunes no son interpretables como variables en sí, sino como factores subyacentes que son producto de una estimación proveniente de variables observables, por lo que la interpretación no es directa, no así el signo, el cual nos indica su contribución, en este caso, las relaciones de cointegración a largo plazo sobre las observaciones.

Finalmente, se realiza un ejercicio de verificación en términos estructurales desagregando el indicador financiero FD_FD_IX con ayuda del primer factor subyacente estimado, dado que ambos están altamente correlacionados y también están cointegrados. Se utiliza la técnica de Denton-Cholette para desagregar el indicador financiero y se hace una estimación estilo Cobb-Douglas ampliada con la variable desagregada obteniendo los siguientes resultados (valores p entre corchetes):

Para verificar evidencia de cointegración desde la perspectiva de Engle y Granger (1987), se realiza la prueba ADF sobre   y se concluye que esta es estacionaria, por lo cual también se concluye que hay evidencia de cointegración, es decir, las variables consideradas se relacionan en el largo plazo, en este caso, con la actividad económica. Llama la atención con respecto a la ecuación (11) que los coeficientes asociados a los factores estructurales son similares, no obstante, el valor de , es mayor que los valores sumados asociados a los efectos de los factores subyacentes estimados previamente. En conclusión, este ejercicio verifica que desde la perspectiva de Engle y Granger también hay evidencia en favor de la contribución del sistema financiero en el crecimiento económico en el largo plazo.

5. Conclusiones

Este trabajo contribuye a la discusión sobre el papel que tiene el sistema financiero en el crecimiento económico utilizando una novedosa aplicación empírica para el caso de México. En este sentido, el análisis de factores dinámicos permite concluir que los factores estimados representan consistentemente, en sentido estadístico y económico, la evolución del sistema financiero en el país.

Los factores se relacionan de manera significativa con el crecimiento económico en el largo plazo en el sentido de que cuando las tasas de interés disminuyen y el resto de las variables financieras incluidas en el modelo incrementan se beneficia la actividad económica, sobresaliendo el efecto del Índice de Precios y Cotizaciones, la liquidez y el de la cartera vigente, es decir, un sistema financiero sano. En el corto plazo, cuando hay un choque en el mercado financiero producto de un incremento de la actividad financiera respecto al comportamiento de largo plazo, la actividad económica reacciona positivamente.

Lo anterior es relevante, por ejemplo, para la conducción de política monetaria, pues la literatura en la materia indica que la fijación de controles en las tasas de interés por debajo de los niveles de mercado o la existencia de mecanismos que induzcan este comportamiento conducen, por lo general, a una asignación de crédito por parte del sistema financiero formal, combinada con un floreciente mercado informal formado por consumidores o productores que se prestan entre sí a tasas de mercado. En ese sentido, son importantes iniciativas planteadas por las autoridades financieras, como la Tasa de Interés Interbancaria de Equilibrio (TIIE) de fondeo que busca establecer una tasa de referencia que esté basada en transacciones observadas en el mercado y que el mercado al que hacen referencia exista y sea representativo, y evitar así abusos o manipulaciones como los ocurridos con la tasa LIBOR en el Reino Unido.

Los resultados apoyan también la hipótesis de que el sector financiero es especialmente relevante en un contexto de recuperación económica. Por ejemplo, en el Reporte de estabilidad financiera del Banco de México (2021, pp. 7-9) se encuentra que en las economías emergentes el otorgamiento del crédito es más importante para que la recuperación sea robusta y rápida, y se indica la importancia de mejorar el entorno y fomentar las condiciones de certidumbre para la inversión y la actividad productiva.

Finalmente, para futuras investigaciones, sería conveniente probar otras variables para capturar el efecto de la variable asociada al capital humano, ya que en la estimación de la función Cobb-Douglas, para explicar la contabilidad del crecimiento económico, se encontró que la suma de los coeficientes es menor a la unidad, en particular el coeficiente asociado con dicha variable es pequeño.

_________________

Fuentes

Aghion, P. y P. W. Howitt. The economics of growth. MIT press, 2008.

Ahn, S. y A. Horenstein. “Eigenvalue ratio test for the number of factors”, en: Econometrica. 81(3), 2013, pp. 1203-1227.

Bai, J. “Inferential theory for factor models of large dimensions”, en: Econometrica. 71(1), 2003, pp. 135–171.

_______ “Estimating cross-section common stochastic trends in nonstationary panel data”, en: Journal of Econometrics. 122(1), 2004, pp.137-183.

Bai, J. y S. Ng. “Determining the number of factors in approximate factor models”, en: Econometrica. 70(1), 2002, pp. 191-221.

_______ “A panic attack on unit roots and cointegration”, en: Econometrica. 72(4), 2004, pp. 1127-1177.

Banco de México (BANXICO). Sistema de Información Económica. 2020.

_______ Reporte de estabilidad financiera, primer semestre del 2021. Banco de México, 2021 (DE) https://bit.ly/397YnOf

Beck, T. The econometrics of finance and growth. Policy Research Working Paper Series 4608. The World Bank, 2008.

_______ Finance and growth: Lessons from the literature and the recent crisis. Prepared for the LSE Growth Commission, 2012.

Bergoeing, R., P. J. Kehoe, T. J. Kehoe y R. Soto. “A Decade Lost and Found: Mexico and Chile in the 1980s”, en: Review of Economic Dynamics. 5(1), 2002, pp. 166-205.

_______ “A Decade Lost and Found: Mexico and Chile in the 1980s”, en: Kehoe, T. J. and Edward C. Prescott. Great Depressions of the Twentieth Century. Minneapolis, Federal Reserve Bank of Minneapolis, 2007, pp. 217-256.

Blanchard, J. y D. Quah. “The Dynamic Effects of Aggregate and Supply Disturbance”, en: The American Economic Review. 79(4), 1989, pp. 653-673.

Blomström, M., R. E. Lipsey y M. Zejan. “Is fixed investment the key to economic growth?”, en: The Quarterly Journal of Economics. 111(1), 1996, pp. 269-276.

Campos, N. y J. Nugent. “Who is afraid of political instability?, en: Journal of Development Economics. 67, 2002, pp. 157-172.

Cermeño, R., J. García y C. González. “Desarrollo financiero y la volatilidad del crecimiento: evidencia de series de tiempo para México y Estados Unidos”, en: Monetaria. 38(2), 2012, pp. 209-250.

Cheng, C. Y., M. S. Chien y C. C. Lee. “ICT diffusion, financial development, and economic growth: An international cross-country analysis”, en: Economic Modelling. 94, 2021, pp. 662-671.

Corona, F., P. Poncela y E. Ruiz. “Determining the Number of Factors After Stationary Univariate Transformations”, en: Empirical Economics. 53(1), 2017, pp. 351-372.

_______ “Estimating non-stationary common factors: implications for risk sharing”, en: Computational Economics. 55(1), 2020, pp. 37-60.

Denton, F. “Adjustment of Monthly or Quarterly Series to Annual Totals an Approach Based on Quadratic Minimization”, en: Journal of the American Statistical Association. 66(333), 1971, pp. 99-102.

Dritsakis, N. y A. Adamopoulos. “Financial Development and Economic Growth in Greece: An Empirical Investigation with Granger Causality Analysis”, en: International Economic Journal 18(4), 2004, pp. 547-559.

Durlauf, S. “Growth econometrics”, en: Handbook of Economic Growth. 1, 2005, pp. 555-677.

Engle, R. y C. Granger. “Co-Integration and Error Correction: Representation, Estimation, and Testing”, en: Econometrica 55(2), 1987, pp. 251-276.

Geweke, J. Latent Variables in Socio-Economic Models. 1977.

Goldsmith, W. Financial Structure and Development. 1969.

Gonzalo, J. y C. W. J. Granger. “Estimation of common long-memory components in cointegrated systems”, en: Journal of Business & Economic Statistics. 13(1), 1995, pp. 27-35.

Gurley, J. y E. Shaw. “Financial Aspects of Economic Development”, en: The American Economic Review. 45(4), 1995, pp. 515-538.

Ibrahim, M. y P. Alagidede. “Effect of financial development on economic growth in sub-Saharan Africa”, en: Journal of Policy Modeling. 40(6), 2018, pp. 1104-1125.

Instituto Mexicano del Seguro Social (IMSS). Consulta dinámica. 2020.

Instituto Nacional de Estadística y Geografía (INEGI). Banco de Información Económica. México, INEGI, 2020.

Johansen, S. “Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Autoregressive Models”, en: Econometrica. 59(6), 1991, pp. 1551-1580.

Jones, C. I. “Time series tests of endogenous growth models, en: The Quarterly Journal of Economics”, 110(2), 1995, 495-525.

Kadhuma, T. A. A. y F. A. Kadhimb. “The Impact of Liberalisation of the Financial Sector on Economic Growth in Iraq for the Period 2004-2018”, en: International Journal of Innovation, Creativity and Change. 14(1), 2020, pp. 709-726.

King, R. y R Levine. “Finance, entrepreneurship and growth”, en: Journal of Monetary Economics. 32(3), 1993, pp. 513-542.

Levine, R. “Finance and growth: theory and evidence”, en: Handbook of Economic Growth. 1, 2005, pp. 865-934.

Lucas Jr, R. E. “On the mechanics of economic development”, en: Journal of Monetary Economics. 22(1), 1988, pp. 3-42.

Lustig, N. “Life Is Not Easy: Mexico’s Quest for Stability and Growth”, en: Journal of Economic Perspectives. 15(1), 2001, pp. 85-106.

Maune, A., E. Matanda y J. Mundonde. “Does financial inclusion cause economic growth in Zimbabwe? An empirical investigation”, en: Acta Universitatis Danubius. Economica. 16(1), 2020, pp. 195-215.

McKinnon, R. Money and Capital in Economic Development. 1973.

Méndez-Heras, L. B., F. Venegas-Martínez y D. E. Linthon-Delgado. “El impacto del crédito bancario sobre el desarrollo humano en México: un análisis de datos panel a nivel estatal, 2004-2016”, en: Ensayos Revista de Economía. 40(1), 2021, pp. 1-28.

Miller, M. “Financial Markets and Economic Growth”, en: Journal of Applied Corporate Finance. 11(3), 1998, pp. 8-13.

Moreno-Brid, J. C., J. Santamaria y J. C. Rivas. “Industrialization and Economic Growth in Mexico after NAFTA: The Road Travelled”, en: Development and Change. 36(6), 2005, pp. 1095–1119.

Onatski, A. “Determining the number of factors from empirical distribution of eigenvalues”, en: The Review of Economics and Statistics. 92(04), 2010, pp. 1004-1016.

Popov, A. “Evidence on finance and economic growth”, en: Handbook of Finance and Development. 2018.

Robinson, J. “The Generalisation of the General Theory”, en: The Generalisation of the General Theory and Other Essays. London, Palgrave Macmillan, 1952, pp. 1-76.

Rodríguez Benavides, D. y F. López Herrera. “Desarrollo financiero y crecimiento económico en México”, en: Problemas del Desarrollo. Revista Latinoamericana de Economía. 40(159), 2010, pp. 41-60.

Rousseau, P. “Historical perspectives on financial development and economic growth”, en: Review, Federal Reserve Bank of St. Louis. 2003, pp. 81-106.

Ruiz, J. L. “Financial development, institutional investors, and economic growth”, en: International Review of Economics & Finance. 54, 2018, pp. 218-224.

Sargent T.J. y C.A. Sims. “Business cycle modeling without pretending to have too much a priory economic theory”, en: New methods in business cycle research. Federal Reserve Bank of Minneapolis, Minneapolis, 1977.

Schumpeter, J. Theorie der wirtschaftlichen Entwicklung (The Theory of Economic Development, traducida por R. Opie. Cambridge, MA, Harvard University Press, 1934). Leipzig, Dunker & Humblot, 1912.

Secretaría de Hacienda y Crédito Público (SHCP). Estadísticas oportunas de finanzas públicas. 2020.

Slesman, L., A. Z. Baharumshah, y W. N. W. Azman-Saini. “Political institutions and finance-growth nexus in emerging markets and developing countries: a tale of one threshold”, en: The Quarterly Review of Economics and Finance. 72, 2019, pp. 80-100.

Stock, J. H. y M. W. Watson. “Testing for common trends”, en: Journal of the American Statistical. 83(444), 1988, pp. 1097-1107.

Svirydzenka, K. Introducing a New Broad-based Index of Financial Development. International Monetary Fund, 2016.

Venegas, F, M. Tinoco y V. Torres. “Desregulación financiera, desarrollo del sistema financiero y crecimiento económico en México: efectos de largo plazo y causalidad”, en: Estudios Económicos. 24(2), 2009, pp. 249-283.

^[1] Encuesta Nacional de Inclusión Financiera (ENIF) 2018, Instituto Nacional de Estadística y Geografía (INEGI).

^[2] Para una revisión profunda de la literatura sobre la relación finanzas-crecimiento económico, se sugiere al lector ver, por ejemplo, Rousseau (2003), Levine (2005) y Beck (2008, 2012).

^[3] Los coeficientes estimados indican efectos modestos; ante un aumento de 10 % en la inversión total se tendría un aumento aproximado de 2.85 % en el PIB real, en el largo plazo, y ante un aumento de 10 % en el nivel de desarrollo financiero se reflejaría en un incremento de 0.8 % del PIB real en el largo plazo.

^[4] Es un modelo de crecimiento endógeno que se emplea en la teoría del crecimiento económico; este utiliza un modelo lineal en el que la producción es una función lineal del capital Y=AK^a L^1-a, donde Y representa la producción total en una economía; A, la productividad total de los factores; K es capital; L, mano de obra; y el parámetro a mide la elasticidad de salida del capital. Para una presentación completa del modelo AK, ver por ejemplo Aghion y Howitt (2008).

^[5] Las correlaciones estimadas entre los indicadores financieros de profundidad financiera (activos líquidos con respecto al PIB, créditos bancarios, activos respecto al crédito privado y crédito privado respecto al PIB) con el crecimiento del PIB per cápita son positivas del orden de 0.56, 0.44, 0.37 y 0.5, respectivamente, y son significativas a 1 por ciento.

^[6]  Situación que se produce cuando un individuo, organización o empresa busca obtener ingresos captando renta económica mediante la manipulación o explotación del entorno político o económico, en lugar de obtener beneficios a través de transacciones económicas y producción de riqueza añadida.

^[7] En inglés, Sample Effective Dependence, se calcula como SED = 1 – |R|^1/(N-1), donde |R| es el determinante de la matriz de correlaciones. Este número está acotado entre 0 y 1, donde mayor significa mayor dependencia lineal multivariada.