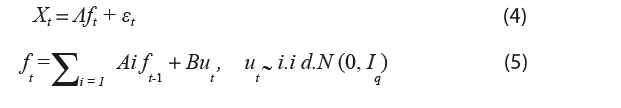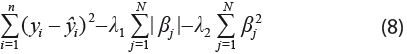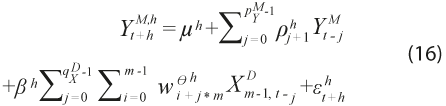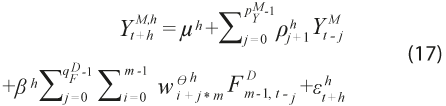Nowcasting of Private Consumption in Mexico: a Combination of Forecasts for the Mexican Case

 

César Leonel García Pérez, Victoria de los Ángeles Díaz Solís, Cynthia Ocampo Castro, Venus Emperatriz Méndez Salazar y Edgar René Benavidez Maruri.*
*Instituto Nacional de Estadística y Geografía (INEGI), leonel.garcia@inegi.org.mx, angeles.solis@inegi.org.mx, cynthia.ocampo@inegi.org.mx, venus.mendez@inegi.org.mx y edgar.benavidez@inegi.org.mx, respectivamente.

 

Vol. 14, Núm. 3– Epub                                 Nowcasting del Consumo…– Epub

En este trabajo se evalúan estimaciones mensuales del Consumo Privado en México mediante el uso de modelos de nowcasting. Con el objetivo de preservar la parsimonia, se aplican técnicas de selección de variables, reducción de dimensionalidad, información en frecuencias mixtas y combinación de pronósticos. Se utilizan modelos de regresión con errores ARMA, de regularización (Elastic Net y Ridge), Muestreo de Datos Mixtos (MIDAS, por sus siglas en inglés) y Factores Dinámicos Jerárquicos (DHFM, por sus siglas en inglés). Los resultados indican que la capacidad predictiva del promedio de los ocho modelos evaluados es estadísticamente superior para la estimación anticipada del Consumo Privado en comparación con la selección de sólo uno de ellos, según la prueba de Diebold-Mariano. Palabras clave: Consumo Privado; factores dinámicos; métodos de penalización; frecuencia mixta; combinación de pronósticos.

This paper evaluates monthly estimates of Private Consumption in Mexico using nowcasting models. In order to preserve parsimony, techniques for variable selection, dimensionality reduction, mixed-frequency information, and forecast combination are applied. Regression models with ARMA errors, penalized linear regression (Elastic Net and Ridge), Mixed-data Sampling (MIDAS), and Dynamic Hierarchical Factors (DHFM) are used. The results indicate that the predictive ability of the average of the eight evaluated models is statistically superior for the early estimation of Private Consumption compared to selecting only one of them, according to the Diebold-Mariano test.                                                       Key words: private consumption; dynamic factors; penalized methods; mixed frequency; combination of forecasts.

Recibido: 25 de octubre de 2022.
Aceptado: 17 de marzo de 2023.

 

1.Introducción

Las decisiones que realizan los formuladores de políticas públicas requieren información oportuna sobre la situación actual de la economía. Esto es más relevante durante periodos volátiles e inciertos, como la crisis del COVID-19, que subraya la importancia de las señales tempranas como auspicios de la dinámica económica. Una de las estimaciones más importantes de la actividad productiva se refiere al principal componente de la Demanda Final (DF): el Consumo Privado (CP).

En México, desde el 2013 hasta el 2021, el CP creció 1.5 % por año. Representa 49 % de la DF y ha contribuido un promedio de 0.8 % a su crecimiento anual. De esta manera, el gasto realizado por los hogares en bienes y servicios de consumo final juega un papel destacado, reflejando la salud de la economía. Sin embargo, como parte del Sistema de Cuentas Nacionales de México (SCNM), el Instituto Nacional de Estadística y Geografía (INEGI) da a conocer los resultados trimestrales aproximadamente 79 días después de concluido el trimestre de referencia a través de los indicadores trimestrales de la Oferta y Demanda, así como un seguimiento mensual mediante el Indicador Mensual del Consumo Privado en el Mercado Interior, base 2013 (IMCPMI) aproximadamente 66 días después de concluido el mes de referencia.

Dada la brecha de oportunidad de seguimiento del IMCPMI, es necesario explorar otras fuentes de información para evaluar la dinámica del consumo de los hogares en el país de manera oportuna. De ahí que este trabajo tiene como objetivo evaluar estimaciones mensuales del CP a través de un conjunto de modelos de nowcasting para ganar oportunidad en la publicación del dato oficial en aproximadamente 30 días. El ejercicio consiste en una estimación puntual del IMCPMI en cifras originales, identificado de ahora en adelante en el documento como Consumo Privado. Los resultados se reportan para cifras originales y desestacionalizadas junto con sus intervalos a un nivel de 95 % de confianza.

Nowcasting es una técnica de estimación que se utiliza para predecir el estado actual o de corto plazo de la economía en tiempo real. Se basa en la combinación de datos recientes y modelos estadísticos para hacer cálculos precisos sobre el crecimiento económico, inflación, consumo, entre otros indicadores, sin esperar a que se publiquen las cifras oficiales. Su objetivo es proporcionar una visión actualizada y exacta de la situación económica en comparación con los métodos tradicionales de estimación.

Para la elaboración del nowcasting del Consumo Privado, se evalúan diferentes modelos basados en investigaciones originadas para pronosticar el Producto Interno Bruto (PIB) trimestral con datos mensuales (Stock y Watson, 2002; Ghysels et al., 2004; Eickmeier y Ng, 2011; Doz y Fuleky, 2020). Los evaluados en este trabajo son: tres de regresión con errores ARMA^[1] —el primero con un componente principal con selección Lasso (ARMA_PCA), el segundo con un factor dinámico de dos etapas con selección Lasso (ARMA_DFM2S) y el tercero con un factor dinámico con selección por mínimos cuadrados parciales (ARMA_DFM)—, dos de regresión lineal con penalización (Elastic Net y Ridge), dos de regresión de muestreo de datos mixtos (MIDAS, por sus siglas en inglés) y, por último, uno de Factores Dinámicos Jerárquicos (DHFM, por sus siglas en inglés).

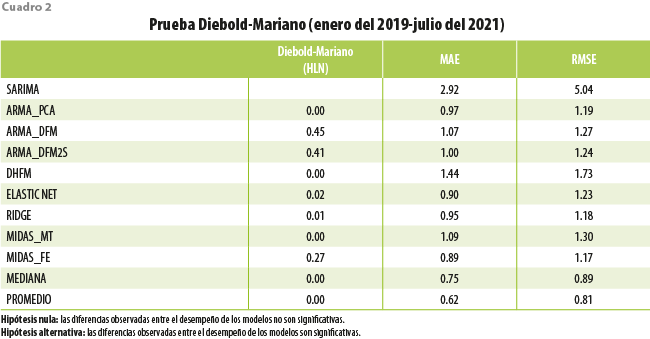
Los resultados de la prueba Diebold-Mariano para la evaluación dentro de la muestra indican que la combinación de los ocho modelos estimados, a partir del promedio simple, ayudó a reducir significativamente los estadísticos de error de predicción —Error Absoluto Medio (MAE, por sus siglas en inglés) y la Raíz del Error Cuadrático Medio (RMSE, por sus siglas en inglés) — frente a la alternativa de solo quedarse con un único modelo. Con base en estos hallazgos, se concluye que el promedio de dichos modelos es el mejor enfoque para generar estimaciones oportunas del Consumo Privado.

La estructura de este trabajo es la siguiente: en la sección dos se presenta la revisión de la literatura; en la tres se muestran los datos utilizados y su tratamiento; en la cuatro se resume la metodología empleada; en la cinco se exhiben los principales resultados; y, por último, en la seis se dan las conclusiones.

 

2. Revisión de literatura

El uso generalizado de los sistemas de pagos electrónicos ha proporcionado nuevas fuentes de datos para el seguimiento de la actividad económica, en especial los recopilados en los de bajo valor. Dichos datos se consideran oportunos, libres de errores de medición y abarcan cheques, transferencias electrónicas de fondos, domiciliaciones y tarjetas bancarias que permiten a los consumidores pagar sus compras al transferir de inmediato fondos desde la cuenta bancaria del titular.

Algunos trabajos empíricos, realizados por los bancos centrales, han presentado evidencia de la utilidad de los sistemas de pagos electrónicos para reducir los errores de previsión del consumo al combinarlo con indicadores tradicionales. Ya sea a través de ecuaciones puente (Galbraith y Tkacz, 2007; Esteves, 2009), regresiones MIDAS (Verbaan et al., 2017) o la comparación de estas con modelos factoriales (Duarte et al., 2017), las investigaciones enfatizan el potencial de esta fuente de datos para la previsión a corto plazo de la tasa de crecimiento interanual del Consumo Privado.

Aunado a los sistemas de pagos electrónicos, el progreso tecnológico ha permitido el desarrollo de otras fuentes de datos utilizables para el seguimiento y la previsión de la actividad económica en tiempo real, en particular, de las decisiones de Consumo Privado, como las tendencias de búsqueda en Google. Al respecto, Gil et al. (2018) hacen uso de un conjunto extendido de indicadores tradicionales, datos de pagos en cajeros automáticos y tendencias de búsqueda en Google para realizar predicciones a corto y mediano plazo del CP español. En línea con otros estudios, estos encuentran que tales datos son indicadores valiosos y que los modelos de frecuencia mixta superan el rendimiento de los que emplean un enfoque de la misma frecuencia.

En México, Corona et al. (2021) han propuesto modelos de nowcasting para estimar el CP y otros indicadores. Gálvez-Soriano et al. (2022) también trabajaron en uno macroeconómico y probaron la hipótesis de que las personas con consumo predecible están en situación de pobreza o trabajan en la informalidad. En este artículo se utilizan datos similares a los empleados por Corona et al. (2020). Sin embargo, se diferencia por incluir información sobre los montos operados con tarjetas en el sistema de pagos de bajo valor y por proponer el uso de regresiones tanto con penalización como MIDAS y factores dinámicos jerárquicos para generar estimaciones mensuales oportunas del Consumo Privado, mientras que el enfoque de combinación de pronósticos se aproxima al propuesto por Gálvez-Soriano (2020) que estima las variaciones trimestrales desestacionalizadas del PIB trimestral.

De acuerdo con la literatura presentada, la principal aportación de este trabajo es la incorporación de información en diferentes frecuencias y la aplicación de un enfoque de combinación de pronósticos para la estimación anticipada del dato oficial del Consumo Privado del INEGI.

 

3. Datos

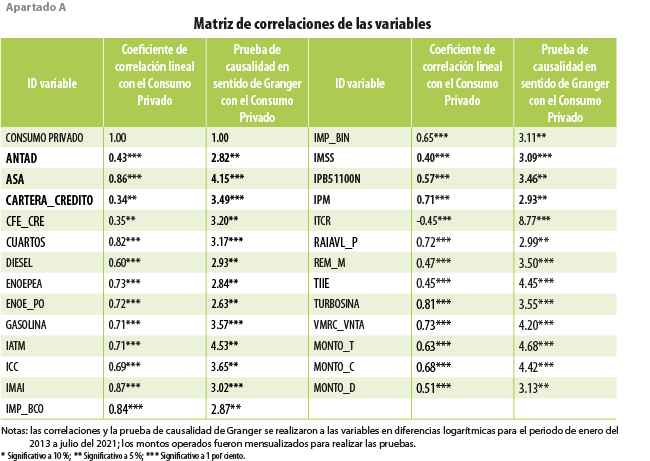
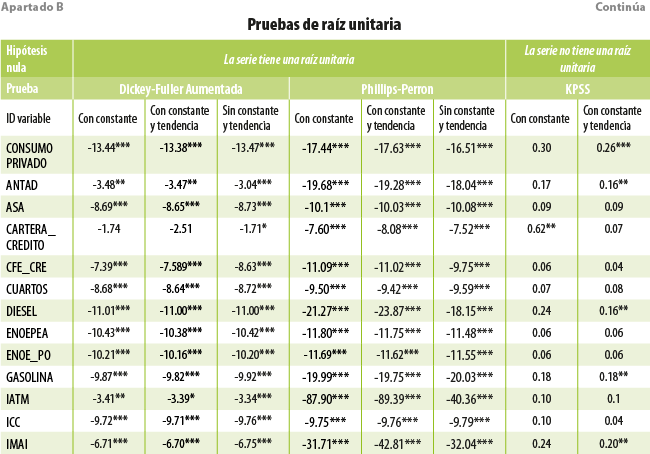
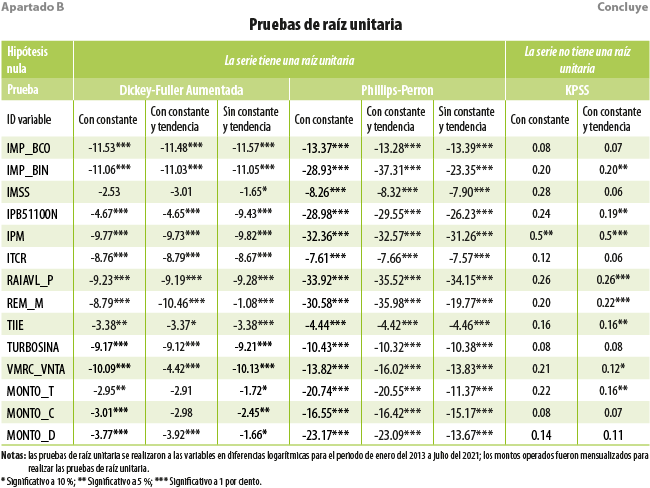
Para generar estimaciones oportunas mensuales del Consumo Privado, se analizaron variables económicas que tienen mayor oportunidad que este indicador y que, además, se relacionan con él este a través de la teoría económica y de manera estadística. La selección del conjunto de variables se realizó con base en el análisis preliminar de la matriz de correlación y de la causalidad en sentido de Granger, lo cual reveló un conjunto de variables potenciales para estimar anticipadamente el CP (ver Anexo).

Las variables utilizadas en los modelos de nowcasting se describen en el cuadro 1. Se incorporaron tanto tradicionales como no tradicionales, de frecuencias mensuales y diarias. El periodo de muestra comprende desde enero del 2013 hasta julio del 2021.

En este trabajo se hace uso de los montos operados a través de tarjetas de débito del sistema de pagos de bajo valor del Banco de México (BANXICO), los cuales ayudan a explicar el consumo realizado por los hogares a partir de sus ingresos disponibles y de los montos operados a través de tarjetas de crédito contribuyendo así a explicar el consumo de los hogares a cuenta de ingresos futuros, ello debido a que el avance tecnológico y la mayor accesibilidad a servicios financieros ha permitido que sea más frecuente poder hacer pagos a través de medios electrónicos. Según la Encuesta Nacional de Inclusión Financiera 2021,^[2] 78 % de la población adulta del país cuenta, o ha contado, con al menos un instrumento financiero. Además, el porcentaje de aquella que tiene más de uno se ha incrementado, lo cual sugiere que la población incluida en el sistema está presentando un mayor uso de estos servicios.

En línea con lo anterior, Jallath y Negrín (2001) afirman que se ha reducido la importancia de los medios de pago tradicionales, mientras que los electrónicos han ganado relevancia y las tarjetas de débito han experimentado un fuerte crecimiento gracias al desarrollo de la red de cajeros automáticos y su aceptación como medio de pago en los puntos de venta. De acuerdo con Campos y Esquivel (2020), el desembolso realizado a través de estos medios no refleja todo el gasto en la economía, pero tampoco es insignificante y puede ayudar a entender los cambios en los patrones de consumo. De esta manera, se enfatiza la importancia del uso de estas variables en este trabajo. Además de la información de los montos operados con tarjetas, se usan variables tradicionales que consisten en datos de la actividad económica publicados mensualmente.

Aunque el enfoque tradicional para hacer pronósticos emplea variables desestacionalizadas, este señala que el componente estacional de cada variable es necesariamente idiosincrático, por lo que al quitarlo se podría generar pérdida de información útil. Por su parte, el uso de las no ajustadas por estacionalidad es recomendable cuando se trabaja con aquellas que presentan interacciones entre la estacionalidad y el ciclo económico. Ejemplo de lo anterior es el Consumo Privado, ya que ajustar los datos de manera estacional podría incurrir en alguna omisión de detalles relevantes sobre la tendencia y los efectos inmediatos de una política pública o un evento inusual que afecte a la economía (Guidetti et al., 2009).

Sobre este último caso, algunos análisis han enfatizado que shocks económicos, como los ocasionados por la contingencia sanitaria del COVID-19, pueden distorsionar el componente irregular de la desestacionalización, provocando sesgos en las variables estacionales (ABS, 2009). Con base en lo anterior, este trabajo se distingue por el uso de series no ajustadas por estacionalidad.

La utilización de variables no ajustadas por estacionalidad se debe, en primer lugar, a la dificultad de adecuar los datos de los montos operados con tarjetas, ya que los métodos actuales de ajuste estacional automático no son aplicables a variables diarias. De acuerdo con Ollech (2021), los métodos empleados por los productores de estadísticas oficiales no facilitan el ajuste estacional y de calendario de series temporales diarias a pesar de que hay un número disponible cada vez mayor de estas; de esta manera, señala que, en la actualidad, no existe un método recomendado oficialmente para ello.

En segundo lugar, aunque se realizaron estimaciones con variables ajustadas estacionalmente (excepto las diarias), se tuvieron errores de predicción más grandes que los obtenidos con las no ajustadas por estacionalidad. Esto podría ser resultado de la combinación de variables mensuales ajustadas y diarias sin ajustar. Por lo tanto, con el objetivo de preservar la robustez de los resultados, se decidió utilizar de manera uniforme los datos, es decir, con variables no ajustadas por estacionalidad o, en otras palabras, en cifras originales.

Por otra parte, los modelos empleados en este trabajo requieren de variables no estacionarias. Para ello, se utilizaron tres tipos de pruebas de raíz unitaria: Dickey-Fuller Aumentada (ADF, por sus siglas en inglés), Phillips-Perron (PP) y Kwiatkowski-Phillips-Schmidt-Shin (KPSS) (ver Anexo). Con base en los resultados de estas, las variables no estacionarias se transformaron a primeras diferencias.

 

4. Metodología

En esta sección se describe cómo generar el nowcasting del Consumo Privado. Primero, se detallan cada una de las metodologías empleadas para la selección de variables: regresión Lasso (Least Absolute Shrinkage and Selection Operator) y la de mínimos cuadrados parciales (PLSR, por sus siglas en inglés). Enseguida, se exponen los métodos de reducción de dimensionalidad: Análisis de Componentes Principales (PCA, por sus siglas en inglés) y los Modelos de Factores Dinámicos de una y dos etapas (DFM y DFM2S, por sus siglas en inglés, respectivamente). Después, se describen los ocho modelos utilizados para producir estimaciones oportunas del CP, los cuales son: tres con errores ARMA, dos con regularización (Elastic Net y Ridge), dos MIDAS y, por último, un DHFM. La estimación oportuna consiste en una combinación de los pronósticos de estos a través de un promedio simple.

 

4.1. Metodologías para la selección de variables y reducción de dimensionalidad

4.1.1. Regresión Lasso

Esta, introducida por Tibshirani (1996), es un método de selección de variables que incorpora penalizaciones en los coeficientes obtenidos por mínimos cuadrados ordinarios con los objetivos de evitar sobreajuste, reducir varianza y minimizar la influencia de las variables menos relevantes. Estima los parámetros β_0, β₁,…,βN, donde N indica el número de variables independientes, que minimizan la suma del cuadrado de los errores.

Los coeficientes del modelo Lasso son aquellos que minimizan:

donde λ es el termino de penalización, la cual tiene el efecto de igualar a 0 algunos de los coeficientes estimados para ciertos valores de λ. Al conseguir que algunos coeficientes sean exactamente 0, Lasso descarta los predictores que no son importantes para el modelo o aquellos cuyos efectos son menos influyentes.

La regresión Lasso se usa para seleccionar las variables utilizadas en la construcción de un componente principal y un factor dinámico de dos etapas. Por otro lado, dado que el monto total operado a través de tarjetas de crédito y débito se integra por 30 variables en su interior según el tipo de establecimiento donde se realizan los pagos con dichos instrumentos (ver Anexo), este método también se emplea para reducir el número mínimo de dimensiones capaces de expresar el máximo de información contenida en los montos operados mediante tarjetas, para la construcción del factor estático utilizado en uno de los modelos MIDAS.

 

4.1.2. PLSR

La regresión por mínimos cuadrados parciales, introducida por Herman Wold (1975), contiene un enfoque de selección de variables que busca una combinación lineal de las que estén más correlacionadas con la respuesta y elimina aquellas que contribuyen poco o nada, lo cual permite explicar de manera más eficiente la varianza en la variable de respuesta.

La regresión por mínimos cuadrados parciales se puede expresar algebraicamente como:

X = TP’ + E_X             (2a) 

Y = UQ’ + E_Y           (2b) 

Sea k ≤ mín { N, M, K } el número de variables a determinar:

1. Las matrices T_{N × K} y  U_{N  X K}  son componentes de X y Y. Además, T  y  U son combinaciones lineales de X y Y.
2. Las matrices P_M × k y QM _× k son las matrices de cargas de X y Y.
3. E_X  y  E_y  son las matrices residuales de X y Y.

Una vez que se han seleccionado las variables, estas se utilizan para construir un factor dinámico.

 

4.1.3. PCA

Técnica que permite reducir N variables predictoras en una cantidad menor de las construidas como combinaciones lineales de las originales.

Sea X_t = (X_1,t, X_2,t,… , X_N,t) con , 1 ≤ t ≤ T , el conjunto de N variables predictoras, las cuales han sido estandarizadas utilizando su media y desviación estándar. Se consideran N combinaciones lineales de X_t como:

lo que resulta en N variables a las que se les llama componentes principales de X. A los coeficientes W_k (1≤ k ≤ N) se les conoce como cargas (o loadings) porque determinan qué tanto contribuye la variable x_it para describir a cada uno de los componentes. El PCA satisface tres condiciones: i) cada uno de los componentes principales tiene la mayor varianza posible, ii) la correlación entre cada uno de estos es igual a 0 y iii) cada una de las cargas tiene norma igual a 1.

Una vez que se ha estimado el componente principal, este se incorpora en el modelo de regresión con errores ARMA.

 

4.1.4. DFM

Introducido por Geweke (1977), Sargent y Sims (1977), y desarrollado para variables económicas por Watson y Engle (1983), Stock y Watson (1988) y Giannone et al. (2008). El DFM expresa al vector X_t de variables observadas como un conjunto de factores no observados o latentes y un término idiosincrático de media 0, donde los primeros están por lo general correlacionados de manera serial (Stock y Watson, 2016). En ellos se recopila información acerca de un conjunto amplio de variables para obtener los factores comunes que explican la varianza de estas, generalmente por el procedimiento de Onatsky (2010), y utilizándolos como regresores para predecir en tiempo real la tasa de crecimiento de la variable objetivo.

Sea X_{t =} (_{X1,t, X2,t, … , XN,t}), con ≤ i ≤ n, el conjunto de N variables predictoras observadas que satisfacen el supuesto de estacionariedad débil. La especificación general del Modelo de Factores Dinámicos es:

donde Λ es la matriz de cargas y su i-ésima entrada es la carga de la serie X_it. La segunda ecuación impone una estructura de proceso Var (p) para los factores f_t. Tanto como ε_t son u_t son normales y se asume que no están correlacionados para ningún rezago, es decir, E[ε_t, u_{t_k}] = 0, para todo k. Por su parte, B es la matriz [I_q, 0_{q×(r _ q)}]´, que hace que el modelo dependa de un subconjunto de r factores en vez de los q iniciales y, de esta manera, evitar sobreajuste. En el caso en que el término idiosincrático esté correlacionado de manera serial, el modelo no está completamente especificado, por lo cual se supone que cada ε_it sigue una autorregresión univariada mediante la siguiente:

donde v_it no está serialmente correlacionado.

 

4.1.5. DFM2S

En el primer paso, los estimadores preliminares de los factores y los parámetros del modelo se calculan a partir de un análisis de componentes principales. En el segundo, se tiene en cuenta la heterocedasticidad de los componentes idiosincrásicos: la dinámica de los factores comunes. Los valores verdaderos de los parámetros ahora se reemplazan por sus estimaciones, y la dinámica de los factores se calcula a partir de las aproximaciones preliminares asociadas de estos. Una vez estimado el componente principal, este se incorpora en el modelo de regresión con errores ARMA.

 

4.2. Modelos para el nowcasting del Consumo Privado

4.2.1 Modelos de regresión lineal con penalización

 

Ridge

Esta añade una penalización sobre la suma de los parámetros de la regresión al cuadrado (Hoerl, 1970). Los coeficientes de Ridge son aquellos que minimizan:

 

donde λ ≥ 0 es un parámetro de ajuste que se determina de forma separada. Cuando λ = 0, el término de penalización, , no tiene efecto y Ridge se reduce a regresión lineal por mínimos cuadrados. Sin embargo, cuando λ tiende al infinito, el impacto de la penalización crece y los coeficientes estimados se aproximan a 0. A diferencia de los mínimos cuadrados, que solo generan una única estimación, Ridge produce una  para cada λ, por lo que la selección adecuada de λ es crucial para obtener una buena estimación, lo cual se logra mediante la validación cruzada o al elegir el valor que minimice el error de predicción en un conjunto de datos de prueba independiente.

 

Elastic Net (Red Elástica)

Esta regresión, desarrollada por Lever et al. (2016) y Zou y Hastie (2005), supera algunas de las limitaciones de Lasso y, al mismo tiempo, aprovecha las bondades de Ridge, dando como resultado una combinación de ambas regresiones.

En este caso, los coeficientes  son aquellos que minimizan:

 

o, equivalentemente, con y 

El grado en que influye cada una de las penalizaciones está controlada por el parámetro a, que está comprendido en el intervalo (0, 1). Nótese que si  a = 0, es una regresión Ridge y si a = 1, es una Lasso. La determinación del parámetro 𝜆 se realizó a través de la validación cruzada de ventana movible.

 

4.2.2 Modelos de regresión con errores ARMA

Se utilizan tres tipos de estos modelos y_t  para definidos de la siguiente manera:

 

donde x_t  es una variable predictora que está construida a partir de los métodos de reducción de variables utilizados (componentes principales y factores dinámicos), por lo que difiere para cada modelo; β, su coeficiente; y z_t, un proceso de ruido blanco.

 

4.2.3. DHFM

Si un panel de datos se puede organizar en bloques utilizando información a priori, entonces la variación entre estos y dentro de los mismos en los datos puede ser capturada por el marco del Modelo de Factor Dinámico Jerárquico. Cada bloque se puede dividir en subbloques para llegar a un modelo multinivel. Su característica principal es que las ecuaciones de transición para los factores en cada nivel tienen intersecciones variables en el tiempo, las cuales dependen de los factores en el siguiente nivel superior. Dichas ecuaciones fueron consideradas por Gammerman y Mignon (1993).

La serie i, en un bloque b, en cada momento t es:

X_ibt = λg_ib (L) g_bt + ex_ibt                                       (11)

     g_bt = Λ_fb (L)ƒ_t + e_gbt                                           (12)

                Φ(L)ƒ_t = u_t                                                   (13)

donde la variable X_ibt dentro de un bloque b está correlacionada debido a los factores comunes ƒ_t o los choques específicos del bloque e_gbt, pero las correlaciones entre bloques solo son posibles a través de ƒ_t, mientras que λ_gib (L) y Φ (L) son rezagos distribuidos de cargas en g_bt y en ƒ_t, respectivamente, y Λ_fb es una matriz triangular inferior con unos en su diagonal. Algunas de las X_it pueden no pertenecer a un bloque y podrían verse afectados los factores comunes de manera directa. Además, se puede permitir que los componentes idiosincrásicos sigan procesos autorregresivos estacionarios:

^Φx_ib (L) e_xibt = ^εx_ibt                                    (14)

^Φg_b (L) e_gbt = ^εg_bt                                     (15)

Este modelo es especialmente útil para monitorear en tiempo real la actividad económica, ya que se filtra el ruido en la medida que llegan datos de forma escalonada. La organización en bloques se realiza utilizando la fecha de publicación de los datos.

 

4.2.4. Modelos MIDAS

En línea con el objetivo de este trabajo, se buscó estimar con base en la información de los montos operados a través de tarjetas de crédito y débito disponible en los sistemas de pago de bajo valor de BANXICO. Debido a que esta se encuentra en frecuencia diaria, en lugar de sincronizar los datos de los montos de tarjetas con los del CP agregándolos temporalmente a una frecuencia mensual, se utiliza un enfoque de regresión de muestreo de datos mixtos para solucionar este problema.

La regresión MIDAS (Ghysels et al., 2004, 2007) es una técnica de estimación que permite que los datos muestreados a diferentes frecuencias se utilicen en la misma regresión, la cual permite la estimación de ecuaciones que explican una variable dependiente de baja frecuencia por variables de alta y sus rezagos, de una manera parsimoniosa y flexible.

MIDAS con Monto Total

Siguiendo el estudio referido de Ghysels et al. (2004, 2007), el modelo MIDAS considera al Consumo Privado como variable dependiente y conceptualiza algunas de las variables tradicionales mostradas en el cuadro 1 como independientes y el monto total operado a través de tarjetas de crédito y débito como variable independiente de alta frecuencia.

Sea   el Consumo Privado y  el monto operado en tarjetas; donde M representa la frecuencia mensual; D, la diaria; y m, el número de transacciones diarias en el mes. Un pronóstico del CP en h periodos en el futuro ha de seguir la forma:

Este modelo tiene una constante, el tradicional término AR con  rezagos mensuales de la variable dependiente  y un término que incorpora veces m rezagos diarios para la variable independiente. El término que multiplica a la variable diaria  merece una atención especial; es el esquema de ponderación que reducirá el número de parámetros a estimar y conducirá a un modelo más parsimonioso en lugar de tener que calcular un coeficiente para cada rezago de alta frecuencia.

Para evitar la proliferación de parámetros, la regresión MIDAS utiliza métodos de ponderación de los coeficientes rezagados para imponer restricciones en la ponderación de la agregación temporal. Lo anterior permite reducir el número de parámetros a estimar, independientemente de la cantidad de rezagos utilizados en el Modelo. Como señalan Ghysels et al. (2004, 2007), existen varios esquemas de ponderación que son útiles para reducir el número de parámetros a estimar; entre estos se incluye: la función de probabilidad Beta normalizada, el polinomio de retardo de Almon y el de Almon exponencial normalizado, las funciones escalonadas y el MIDAS no restringido.

 

MIDAS con un Factor Estático

Una segunda propuesta metodológica se refiere al modelo MIDAS aumentado con selección de variables. Como se mencionó en la sección 4.1.1, se utiliza la regresión Lasso con el objetivo de reducir el número de variables que integran el monto total operado por tarjetas; posteriormente, con aquellas que se han elegido, se construye un factor estático, lo que en suma es una combinación de lo planteado en la sección anterior. El Factor Estático (FE) es una combinación lineal de las variables determinadas por medio de la regresión Lasso que explica la mayor cantidad posible de la varianza total de los datos. La expresión algebraica para un FE puede escribirse como F = XA, donde F es el factor; X, la matriz de variables originales; y A, la matriz de cargas factoriales.

Este esfuerzo por combinar la selección de variables y la regresión MIDAS se debe a que, de acuerdo con Marsilli (2014), una elección adecuada de variables explicativas, independientemente de sus frecuencias de muestreo, tiene un impacto importante en el rendimiento del método de pronóstico. De esta manera, hacerlo en frecuencias mixtas se basa en la idea de que el uso de predictores bien depurados ayuda a mejorar de forma significativa la calidad de las estimaciones.

Así, es posible formalizar el Modelo de la siguiente manera: sea el Consumo Privado y  el factor de los montos operados en tarjetas; donde M representa la frecuencia mensual; D, la frecuencia diaria; y m, el número de observaciones diarias en el mes. Un pronóstico del CP en h periodos en el futuro adopta la estructura:

donde   corresponde al factor de alta frecuencia que explica la mayor variación de todo el conjunto de variables en el que se desglosan los montos operados.

 

5. Resultados

Para los modelos de penalización, Ridge y Elastic Net, se seleccionó un subconjunto de variables del cuadro 1, de manera que se conservara la mayor cantidad de información distinta entre ellas y la elección fuese lo más adecuada posible. Posteriormente, para cada modelo, se determinó la 𝜆 óptima y, con ello, se ponderó cada variable. Para ambos, se utilizó la validación cruzada de ventana movible y varias iteraciones para refinar el parámetro 𝜆. Por último, una vez determinados los parámetros a y λ , la estimación de β  para Ridge y Elastic Net se realizó mediante el Método de Máxima Verosimilitud Penalizada a través de técnicas de optimización convexa (Friedman et al., 2010).

Para el caso de los modelos de regresión con errores ARMA, se construyeron tres a partir de la generación de tres variables explicativas diferentes obtenidas con las metodologías de reducción de dimensionalidad (uno con un componente principal, uno con factor dinámico y otro más con factor dinámico en dos etapas), obteniendo ARMA_PCA, ARMA_DFM y ARMA_DFM2S. La identificación de los valores de  y  se realizó con base en el criterio de información de Schwarz (SIC, por sus siglas en inglés).

Por su parte, para la estimación del DHFM, se inició con un panel balanceado con las variables del cuadro 1. Estas se organizan utilizando datos previos sobre su estructura en tres bloques de información, variando la clasificación de cada una de las variables de manera que se logre el mejor ajuste en cada mes. Cabe señalar que este modelo utilizó la información disponible en el Índice de Movilidad de Google con el objetivo de modelar el impacto en el Consumo Privado que provocaron las medidas de contención de movilidad implementadas durante la contingencia por COVID-19 en México, a la cual se le estableció un valor constante de 100 al periodo anterior a la pandemia.

Respecto a los modelos MIDAS, se realizó la estimación usando la variable de monto total operado en tarjetas y el factor estático construido a partir de las variables que componen al monto total, por lo que se obtienen los MIDAS_MT y MIDAS_FE, respectivamente. Como se mencionó en la sección 4, se consideraron diferentes funciones de ponderación para los modelos MIDAS. En el caso del MIDAS_MT, las Beta y Almon se desempeñaron de manera consistente, mientras que el rendimiento de la función escalonada fue más errático. Sin embargo, fue la ponderación de Almon la sobresaliente en comparación con el resto al presentar menores errores de predicción. Para el caso de MIDAS_FE, se observó que los resultados varían de forma mínima entre funciones de ponderación empleadas. No obstante, el modelo que se destacó del resto fue el que se ajustó con la función Almon exponencial. El número de rezagos óptimos para ambos MIDAS fue seleccionado con base en el SIC.

 

5.1. Estimaciones oportunas del CP dentro de la muestra

Para evaluar el desempeño relativo de los ocho modelos de nowcasting y generar estimaciones oportunas del Consumo Privado, se realizó un ejercicio de cálculo recursivo dentro de la muestra permitiendo agregar una nueva observación cada nuevo mes a estimar. El periodo de evaluación dentro de esta abarca desde enero del 2019 hasta julio del 2021, lo que corresponde a 31 meses estimados. Siguiendo la literatura relacionada, se considera como referencia el Modelo Autorregresivo Integrado de Media Móvil Estacional (SARIMA).

Para la evaluación de las estimaciones dentro de la muestra, los ocho modelos antes mencionados se estiman y prueban empíricamente con el fin de evaluar su desempeño para estimar valores conocidos del Consumo Privado. Siguiendo la sugerencia de Kennedy (2008) sobre cómo la combinación de pronósticos de diferentes modelos produce, en general, un mejor pronóstico, se aplicó un cálculo de promedio ponderado con pesos iguales, también se tomó la mediana de los ocho modelos para mejorar la precisión de los resultados, los cuales se consideran como estimaciones adicionales.

Para evaluar la capacidad predictiva de cada modelo, se utilizó la prueba Diebold-Mariano bajo el enfoque de Harvey-Leybourne-Newbold (HLN) para muestras pequeñas (Harvey et al., 1997). Adicionalmente, se utilizan los índices estadísticos MAE y RMSE como criterio de evaluación de los modelos de nowcasting del Consumo Privado.

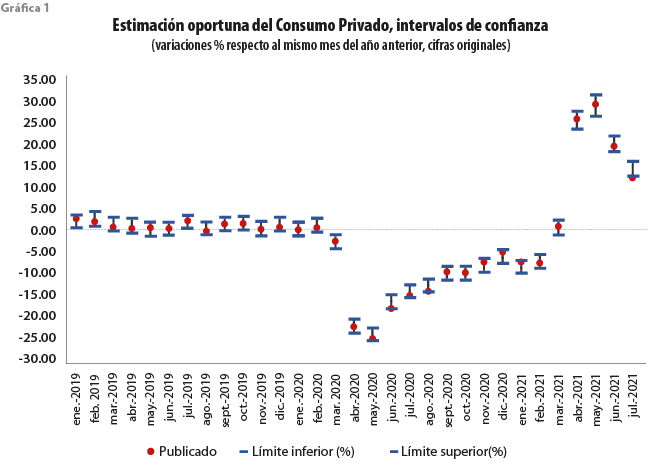
El cuadro 2 resume los valores p obtenidos por la prueba Diebold-Mariano respecto al SARIMA, el cual sirve para contrastar los resultados de la prueba, que muestran que se rechaza la hipótesis nula a un nivel de significancia de 5 % de igual desempeño para ARMA_DFM, ARMA_DFM2S y MIDAS_FE, mientras que el resto de los modelos tienen un desempeño similar en términos de su capacidad predictiva, ya que no existe suficiente evidencia para afirmar que uno es significativamente mejor que el otro, según la prueba HLN. Es importante señalar que las estimaciones generadas por el promedio y la mediana mostraron mejor desempeño que cualquier otro modelo de nowcasting en cada uno de los criterios de evaluación. En particular, el resultado obtenido a través del promedio de los ocho modelos registra un error absoluto medio más pequeño (MAE = 0.62) frente al del de referencia (MAE = 2.92). Mientras tanto, al observar la gráfica 1, los intervalos a 95 % de confianza, obtenidos para las estimaciones dentro de la muestra, lograron capturar 94 % de las variaciones anuales observadas del CP, esto es, 29 de los 31 meses. Con base en estos resultados, se concluye que el promedio de los ocho modelos evaluados es estadísticamente superior para la estimación anticipada del Consumo Privado en comparación con la selección de solo uno de ellos.

 

5.2. Nowcasting del Consumo Privado en tiempo real (fuera de la muestra)

De acuerdo con los resultados obtenidos de la evaluación dentro de la muestra en la sección anterior, se verifica que el enfoque de combinación de pronósticos, a partir del promedio simple de los ocho modelos, provee resultados más precisos del Consumo Privado que el resto de los modelos individuales analizados. Por lo tanto, se realizaron estimaciones en tiempo real para el periodo comprendido entre agosto y diciembre del 2021. Es importante señalar que todos los resultados en esta sección se basaron en una fecha de corte actualizada del CP hasta diciembre del año en mención. Esta consideración resulta relevante debido a que el INEGI realiza revisiones periódicas de sus indicadores mensuales.

El cuadro 3 presenta los pronósticos en tiempo real del Consumo Privado en variaciones anuales originales para los últimos cinco meses del 2021, así como sus intervalos a un nivel de confianza de 95 por ciento. Para los resultados en cifras originales, se sigue el enfoque mencionado anteriormente: para cada mes se obtienen los pronósticos de los ocho modelos descritos en secciones anteriores y, después, se promedian. Debido a que los residuos de todos los modelos presentan ruido blanco y una distribución normal (ver Anexo), el intervalo de confianza para cada uno está dado por:

Posteriormente, los ocho pares de intervalos se promedian para obtener los intervalos a 95 % de confianza de la estimación oportuna.

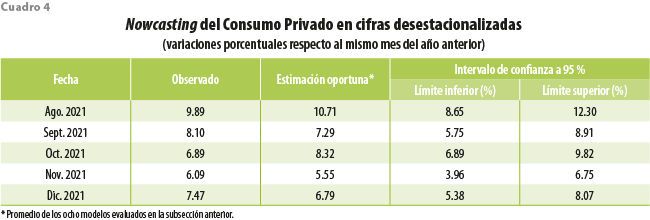
El cuadro 4 muestra la estimación oportuna, pero en variaciones anuales ajustadas por estacionalidad. Para los resultados en cifras desestacionalizadas, se emplea el mismo procedimiento utilizado por el INEGI para el IMCPMI. En este sentido, se realiza con el paquete estadístico X-13ARIMA-SEATS aplicando la metodología de promedios móviles y modelos RegARIMA. La especificación del ajuste estacional puede cambiar conforme se van incluyendo nuevas observaciones, por lo que los parámetros de este son reestimados, actualizando de esta forma la serie desestacionalizada.

La estimación oportuna de las variaciones anuales del Consumo Privado obtenidas para los últimos cinco meses del 2021 responde a la baja base de comparación en relación con el 2020 que resultó de las distorsiones en los patrones de consumo provocadas por la pandemia de COVID-19. De acuerdo con las estimaciones oportunas del CP en cifras desestacionalizadas presentadas en el cuadro 4, se experimentó una recuperación durante los últimos cinco meses del 2021, ya que agosto, septiembre, octubre, noviembre y diciembre arrojaron variaciones anuales moderadas de 10.71, 7.29, 8.32, 5.55 y 6.79 %, respectivamente, lo que se tradujo en crecimientos mensuales (0.04, 0.03, 1.47, 0.60 y 1.16 %, en ese mismo orden). Lo anterior, indica que el Consumo Privado se vio favorecido por una mayor apertura de actividades económicas y un relajamiento de las restricciones a la movilidad de las personas por la tendencia descendente del número de contagios por COVID-19, la recuperación del empleo y la mayor llegada de remesas familiares.

Si bien la recuperación del Consumo Privado a finales del 2021 exhibe señales del fortalecimiento de la demanda interna, al comparar los resultados para diciembre del 2021 con el nivel en enero del 2020, previo al inicio de la pandemia en el país, se observa que el consumo todavía se encontraba rezagado en poco más de un punto porcentual. Con esto se concluye que en el 2021 no se logró una recuperación completa para este indicador.

Por último, en la gráfica 2 se muestran las estimaciones oportunas correspondientes a los últimos cinco meses del 2021 (sombreado con azul oscuro) y sus intervalos de confianza a 95 % para cada mes (líneas punteadas).

 

 

6. Conclusiones

Este trabajo busca generar estimaciones mensuales del Consumo Privado en México con el objetivo de tener información oportuna acerca del componente más grande de la Demanda Agregada. En línea con dicho objetivo se evalúan los resultados de los ocho modelos de nowcasting para un periodo dentro de la muestra comprendido entre enero del 2019 y julio del 2021 con el fin de compararlos frente a valores publicados del IMCPMI. Siguiendo a la literatura, se incluye un modelo SARIMA a manera de referencia.

Cabe destacar que el periodo de evaluación dentro de la muestra contempla la emergencia sanitaria por COVID-19, lo cual constituye un desafío para los pronósticos que pone a prueba el contenido informativo de las variables utilizadas, así como la capacidad predictiva de cada modelo en un contexto de volatilidad en la economía mexicana.

Previo a la estimación, se priorizó el uso de variables correlacionadas de manera teórica y estadística con el Consumo Privado, las cuales se caracterizan por estar relacionadas con el gasto en bienes y servicios de consumo de los hogares, mientras que se aprovecha la información disponible en otro conjunto de variables no tradicionales y de alta frecuencia, como los montos operados con tarjetas y el Índice de Movilidad de Google.

Debido a que este documento analiza el uso de diferentes modelos de Nowcasting con el objetivo de aprovechar la información que está altamente correlacionada con el Consumo Privado en México, se emplearon técnicas de selección de variables (Lasso y PLSR), reducción de dimensionalidad (componentes principales y factores dinámicos y estáticos), información de alta frecuencia (montos operados con tarjetas e Índice de Movilidad de Google), además de combinación de pronósticos.

Los modelos evaluados en este trabajo fueron: tres regresiones con errores ARMA —el primero con un componente principal con selección Lasso (ARMA_PCA), el segundo con un factor dinámico de dos etapas con selección Lasso (ARMA_DFM2S) y el tercero con un factor dinámico con selección por mínimos cuadrados parciales (ARMA_DFM)—, dos de regresión lineal con penalización (Elastic Net y Ridge), dos de regresión de muestreo de datos mixtos (MIDAS_MT y MIDAS_FE) y, por último, un DHFM.

Los resultados de la prueba Diebold-Mariano indican que los modelos que generan menores criterios de evaluación son ARMA_PCA, Ridge y MIDAS_FE. Asimismo, se encontró que la combinación de los pronósticos de los ocho modelos evaluados, a partir del promedio simple, ayudó a reducir significativamente los estadísticos de error de predicción MAE y RMSE frente a la alternativa de solo quedarse con un único modelo. Con base en estos resultados, se concluye que el promedio de los ocho modelos, en relación con las metodologías aplicadas, es el mejor enfoque para generar estimaciones oportunas mensuales del Consumo Privado.

Finalmente, se realiza un ejercicio de pronósticos en tiempo real del Consumo Privado para el periodo comprendido entre agosto y diciembre del 2021. En general, los resultados obtenidos para el análisis demostraron ser robustos y el poder predictivo acertado. De esta manera, se advierte que la metodología presentada en este documento ofrece estimaciones oportunas, precisas y confiables del CP un mes antes de la publicación oficial del INEGI, incluso en una economía emergente durante periodos volátiles e inciertos, como la crisis sanitaria por COVID-19.

___________

Fuentes

Australian Bureau of Statistics (ABS). “When it’s not business-as-usual: Implications for ABS time series”, en: Australian Economic Indicators; Australian Bureau of Statistics. Australia, 2009, pp. 3-13. (DE): bit.ly/3tHHl3z.

Campos-Vázquez, R. M. y G. Esquivel. “Niveles y patrones de consumo en la era del COVID-19”, en: Revista Nexos en Línea. 2020 (DE) bit.ly/3P1kwiv.

Comisión Nacional Bancaria y de Valores (CNBV). Encuesta Nacional de Inclusión Financiera (ENIF) 2021: Reporte de resultados. 2022 (DE) bit.ly/ENIFCNBV.

Corona, F., G. González-Farías y J. López-Pérez. A nowcasting approach to generate timely estimates of Mexican economic activity: An application to the period of COVID-19. 2020 (DE) arXiv preprint arXiv:2101.10383.

Corona, F., J. López-Pérez y P. Orraca. “Estimaciones oportunas para algunas variables relevantes de la coyuntura económica de México: implicaciones de corto plazo”, en: Realidad, Datos y Espacio Revista Internacional de Estadística y Geografía. 12(3), México, 2021, pp. 28-49.

Doz, C. y P. Fuleky. “Dynamic Factor Models”, en: Macroeconomic forecasting in the era of big data. 2020, pp. 27-64.

Duarte, C., P. M. Rodrigues y A. Rua. “A mixed frequency approach to the forecasting of private consumption with ATM/POS data”, en: International Journal of Forecasting. 33(1), Portugal, 2017, pp. 61-75.

Eickmeier, S. y T. Ng. “Forecasting national activity using lots of international predictors: An application to New Zealand”, en: International Journal of Forecasting. 27(2), Nueva Zelanda, 2011, pp. 496-511.

Esteves, P. Are ATM/POS data relevant when nowcasting private consumption? Working Papers w200925. Banco de Portugal, Economics and Research Department, 2009.

Friedman, J., T. Hastie y R. Tibshirani. “Regularization Paths for Generalized Linear Models”, en: Journal of Statistical Software. 33(1), 2010, pp. 1-22.

Galbraith, J. y G. Tkacz. “Electronic transactions as high-frequency indicators of economic activity”, en: Staff Working Papers. 7(58), Bank of Canada, 2007.

Gálvez-Soriano, O. D. J. “Nowcasting Mexico’s quarterly GDP using factor models and bridge equations”, en: Estudios Económicos. 35(2), 2020, pp. 213-265.

Gálvez-Soriano, O. D. J., M. Ramírez-Loyola y D. Vega Valdivia. “Informalidad, pobreza y consumo en México: Evidencia empírica entre 1993 y 2019”, en: Revista Mexicana de Economía y Finanzas. 17(2), 2022.

Gammerman, D. y H. S. Mignon. “Dynamic Hierarchical Models”, en: Journal of Royal Statistical Society Series B55. 1993, pp. 629-642.

Geweke, J. “The Dynamic Factor Analysis of Economic Time Series Models Latent Variables”, en: Socioeconomic Models. North Holland, 1977, pp. 365-83.

Ghysels, E., P. Santa-Clara y R. Valkanov. “The MIDAS touch: Mixed data sampling regression models”, en: University of North Carolina and UCLA. Discussion Paper. 2004.

Ghysels, E., A. Sinko y R. Valkanov. “MIDAS Regressions: Further Results and New Directions”, en: Econometric Reviews. 26(1), 2007, pp. 53-90.

Giannone, D., L. Reichlin y D. Small. “Nowcasting: The real-time informational content of macroeconomic data”, en: Journal of Monatary Economics. 2008, pp.665-676.

Gil, M., J. J. Pérez, A. J. Sánchez Fuentes y A. Urtasun. Nowcasting private consumption: traditional indicators, uncertainty measures, credit cards and some internet data. Working Paper No. 1842. Banco de España, 2018.

Guidetti, E., G. Gyomai y F. Spinelli. “Is it necessary to seasonally adjust business and consumer confidence series?”, en: Leading Indicators draft OCDE. 2009 (DE) bit.ly/46ZPjn1.

Harvey, D., S. Leybourne y P. Newbold. “Testing the equality of prediction mean squared errors”, en: International Journal of forecasting. 13(2), 1997, pp. 281-291.

Hoerl, A. “Ridge Regression: Biased Estimation for Nonorthogonal Problems”, en: Technometrics. 12(1), 1970, pp. 55-67.

Jallath, E. y J. Negrín. Evolución y estructura de los medios de pago distintos al efectivo en México. BANXICO, 2021 (DE) DOI:10.36095/banxico/di.2001.04.

Kennedy, P. A guide to econometrics. John Wiley & Sons, 2008.

Lever, J., M. Krzywinski y N. Altman. “Regularization”, en: Nat Methods. 13(10), 2016, pp. 803-805.

Marsilli, C. “Mixed-Frequency Modeling and Economic Forecasting”, en: Université de Franche-Comté. 2014.

Moench. E. “Dynamic Hierarchical Factor Models”, en: Federal Reserve Bank of New York Staff Reports. 412, 2009.

Ollech, D. “Seasonal Adjustment of Daily Time Series”, en: Journal of Time Series Econometrics. 13(2), 2021, pp. 235-264 (DE) bit.ly/3Sffj9M.

Onatsky. A. “Determining the number of factors from empirical distribution of eigenvalues”, en: The Review of Economics and Statistics. 92(4), 2010, pp. 1004-1016.

Sargent, T. y C. Sims. “Business cycle modeling without pretending to have too much a priori economic theory”, en: New methods in business cycle research. 1977, pp. 145-168.

Stock, J. y M. Watson. A Probability Model of the Coincident Economic Indicators. 1988.

_______ “Macroeconomic forecasting using diffusion indexes”, en: Journal of Business & Economic Statistics. 20(2), 2002, pp. 147-162.

_______ “Factor Models and Structural Vector Autoregressions in Macroeconomics”, en: Taylor, J. y H. Uhlig (eds.). Handbook of Macroeconomics 2. Elsevier, 2016.

Tibshirani, R. “Regression shrinkage and selection via the Lasso”, en: Journal of the Royal Statistical Society. 58(1), 1996, pp. 267-288.

Verbaan, R., W. Bolt y C. van der Cruijsen. Using debit card payments data for nowcasting Dutch household consumption. Nederlandsche Bank Working Paper No. 571. 2017.

Watson, M. W. y R. F. Engle. “Alternative algorithms for the estimation of dynamic factor, mimic and varying coefficient regression models”, en: Journal of Econometrics. 23(3), 1983, pp. 385-400.

Wold, Herman. “Path models with latent variables: The NIPALS approach”, en: Quantitative sociology. Academic Press, 1975, pp. 307-357.

Zou, H. y T. Hastie. “Regularization and variable selection via the Ridge”, en: Journal of the Royal Statistical Society, Series B. 67(2), 2005, pp. 301-320.

 

Anexo

 

 

^[1] Autoregressive Moving Average, por sus siglas en inglés.

^[2] Programa de información llevado a cabo por la Comisión Nacional Bancaria y de Valores (CNBV) y el INEGI.