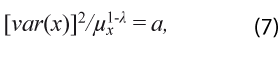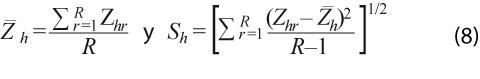Selección de transformación potencia en los indicadores trimestrales de actividad económica estatal: implicaciones en el análisis de factores

 

Power transformation selection in quarterly indicators of state economic activity:
implications for factor analysis

 

Francisco de Jesús Corona Villavicencio y Jesús López Pérez*
* Instituto Nacional de Estadística y Geografía, franciscoj.corona@inegi.org.mx y jesus.lopezp@inegi.org.mx, respectivamente.

Nota: nuestro agradecimiento a los valiosos comentarios de Juan Martínez, Liliana Martínez y Oziel Martínez de la Dirección de Estudios Econométricos del INEGI, los cuales nos ayudaron a hacer de este un mejor trabajo; también, nuestra gratitud por sus aportaciones durante todo el desarrollo de esta investigación a Víctor M. Guerrero del Departamento de Estadística del ITAM; y, por último, a Gerardo Leyva Parra, director general adjunto de Investigación del INEGI.

Vol. 12, Núm. 1 – Epub                                                   Selección de transformación… – Epub

En este trabajo se presenta un análisis empírico de las implicaciones que tiene la selección de la transformación potencia en el proceso de ajuste estacional para el Indicador Trimestral de la Actividad Económica Estatal (ITAEE). En primera instancia se comparan, en sentido estadístico, las series obtenidas a través de los modelos que arroja de manera automática el X-13ARIMA-SEATS, los de desestacionalización del Instituto Nacional de Estadística y Geografía y una alternativa de modelación que selecciona el tipo de transformación potencia a través del procedimiento de Guerrero (1993); las diferentes pruebas estadísticas indican que hay indicios en favor del enfoque alternativo. Posteriormente, se realiza la estimación de factores comunes con los tres grupos de series desestacionalizadas, la cual muestra que existen ligeras diferencias entre los tres enfoques, la más importante, en relación con el número de factores estimado, donde existe uno más cuando se utilizan las series desestacionalizadas con el nuevo enfoque sugerido. Palabras clave: errores idiosincráticos; factores comunes; series de tiempo aditivas; series de tiempo multiplicativas; X-13ARIMA-SEATS.

This paper presents an empirical analysis of the implications of the selection of the power transformation in the seasonal adjustment process for the Quarterly Indicator of State Economic Activity (ITAEE). First, a statistical comparison is made between the series obtained through the models automatically produced by X-13ARIMA-SEATS, the seasonal adjustment models of the National Institute of Statistics and Geography and an alternative model that selects the type of power transformation through Guerrero’s (1993) procedure; the different statistical tests indicate that there are indications in favor of the alternative approach. Subsequently, the estimation of common factors is carried out with the three groups of seasonally adjusted series, which shows that there are slight differences between the three approaches, the most important one, in relation to the number of estimated factors, where there is one more when using the seasonally adjusted series with the new suggested approach. Key words: idiosyncratic noises; common factors; additive time series; multiplicative time series; X-13ARIMA-SEATS.

Aceptado: 12 de diciembre de 2019.
Recibido: 7 de octubre de 2020.

 

Introducción

El objetivo estadístico del procedimiento de desestacionalización es proporcionar series de tiempo libres de patrones sistemáticos aludidos a su frecuencia temporal, es decir, sin movimientos repetitivos año con año de carácter semestral, trimestral, mensual, quincenal, etc., según la serie de tiempo. El objetivo, desde un punto de vista económico, es que estas permitan realizar un análisis más certero sobre el comportamiento conceptual de la variable, importante para la formulación de políticas públicas; por ejemplo, puede ser significativo estudiar y entender la dinámica del Producto Interno Bruto (PIB) para el diseño de políticas contracíclicas en momentos en los cuales la economía decrece o bien crece, pero de manera mínima. Para estos fines, es de interés enfocarse en la serie del PIB trimestral desestacionalizado, la cual permite centrarse en la componente de tendencia-ciclo más los efectos irregulares, libre de movimientos de naturaleza no económica que influyen sobre el comportamiento de dicha serie. De esta forma, las fluctuaciones del PIB reflejan de mejor manera los efectos de carácter económico, como las políticas macroeconómicas. Lo mismo puede ser para las series de desempleo, ventas y producción industrial, entre otras.

En México, el Instituto Nacional de Estadística y Geografía (INEGI) es el organismo encargado de desestacionalizar las series de tiempo de manera oficial, para lo cual utiliza como base el X-13ARIMA-SEATS del Census Bureau de los Estados Unidos de América. El detalle de dicha metodología aplicada para el caso de nuestro país puede ser consultado en Guerrero et al. (2018).

Este procedimiento se basa en varios pasos que podemos sintetizar en: 1) visualizar patrones gráficos de la serie, 2) realizar pruebas formales para determinar si la serie de tiempo tiene patrones estacionales, 3) establecer si esta es aditiva o multiplicativa, 4) determinar los ajustes previos (efectos calendario y outliers), 5) construir y estimar el modelo ARIMA con la metodología de Box-Jenkins, 6) seleccionar y aplicar los filtros estacionales, 7) verificar que los resultados cumplan los supuestos y, en su caso, hacer ajustes y 8) determinar si es necesario aplicar el método indirecto de desestacionalización para el caso de conjunto de series agregadas.

Enfocándonos en el punto 3, este se encuentra directamente relacionado con métodos de selección de transformación potencia al estilo Box y Cox (1964) en series de tiempo, donde no solo nos limitamos a la disyuntiva entre mantener lineal la serie de tiempo o aplicarle logaritmos, sino que puede extenderse también, por ejemplo, para transformaciones cuadráticas o cúbicas. No obstante, dentro del contexto del X-13ARIMA-SEATS sí requerimos enfocarnos solo en determinar si es aditiva o bien, si es necesario estabilizar la varianza cuya dependencia es proporcional a su media, es decir, realizar transformación logarítmica con lo cual se determina que es multiplicativa. La manera en cómo se realiza esto está relacionada con seleccionar aquel modelo que tiene un menor valor en el criterio de información de Akaike (AIC); intrínsecamente, buscamos minimizar la varianza residual o maximizar el logaritmo de la función de verosimilitud invariante a la magnitud de la serie en el modelo ARIMA, lo cual es válido si suponemos que los modelos subyacentes tienen la misma cantidad de parámetros. Este procedimiento suele dar resultados razonables en la práctica (Shulman y McKenzie, 1984).

Por otra parte, Guerrero (1993), bajo pocos supuestos en los primeros dos momentos de la serie de tiempo, propone un criterio para encontrar la constante que minimiza el coeficiente de variación en esta, el cual es visto como una extensión a la transformación Box y Cox (1964) y representa una alternativa natural para identificar de qué tipo es; en otras palabras, permite decidir si se realiza o no la transformación logarítmica bajo una búsqueda restringida de la constante que minimiza el coeficiente de variación. Aunque existen representaciones híbridas (entre aditivas y multiplicativas) que pueden verse en Dagum (1980), Findley et al. (1998) y Ladiray y Quenneville (2000-2001), no son materia de análisis de este trabajo, ya que no se utilizan con frecuencia en la práctica.

Nótese que el uso del AIC para decidir si una serie es aditiva y multiplicativa (en el contexto del X-13ARIMA-SEATS) puede resultar erróneo, dado que la maximización del logaritmo de la función de verosimilitud depende de la distribución de los errores del modelo paramétrico subyacente que, en términos prácticos, suele verificarse con pruebas de normalidad, dados los supuestos del modelo ARIMA. Lo anterior implica que si la serie es multiplicativa (es decir, procede de un proceso generado con distribución Log-normal) estaría siendo comparada como si fuese generada por un proceso con distribución normal (Guerrero et al., 2018, 79). Al momento no se encuentra en la literatura una investigación que compare métodos de selección de transformación potencia en el proceso de desestacionalización.

En consecuencia, dada la importancia del uso de las series desestacionalizadas con el método X-13ARIMA-SEATS y la relevancia del Indicador Trimestral de Actividad Económica Estatal (ITAEE) para analizar la coyuntura económica como variables proxy al PIB trimestral por entidad federativa, en este trabajo pretendemos cumplir con los siguientes objetivos: 1) comparar estadísticamente los modelos que arroja de manera automática el X-13ARIMA-SEATS, los modelos elaborados por el INEGI y los que seleccionan la transformación potencia a través del procedimiento de Guerrero (1993) para este conjunto de series de tiempo y, una vez desestacionalizadas las series con los tres enfoques, 2) analizar las implicaciones con base en un análisis de factores, esto con el fin de contribuir a la explicación de las variaciones a corto plazo de cada una de las series de tiempo.

Lo que resta de este documento está organizado como sigue: la sección dos resume las metodologías abordadas en este trabajo para realizar las transformaciones potencia de las series de tiempo; la siguiente presenta con detalle la aplicación de los métodos descritos previamente y los resultados de la estimación de factores comunes; en el apartado final se muestran las conclusiones y recomendaciones.

Metodología de transformación potencia

Podemos definir a la serie de tiempo por desestacionalizar como Y_t, la cual, en el contexto del X-13ARIMA-SEATS, puede ser de frecuencia mensual o trimestral y presenta los siguientes componentes: la tendencia-ciclo (T_t) que incluye los movimientos de largo plazo y las fluctuaciones alrededor de estos; la estacionalidad (E_t) que contiene efectos calendario y patrones sistemáticos dados por la frecuencia temporal de la serie; y la irregularidad (I_t) que, para nuestros fines, se supone ruido blanco.

La manera de ligar Y_t con sus respectivas componentes viene dada, primero, por la siguiente representación aditiva:

 Y_t = T_t + E_t + I_t.          (1)

Por otra parte, la descomposición multiplicativa puede ser expresada como:

Y_t = T_t × E_t × I_t.          (2)   

Nótese que, en este caso, se puede representar a la ecuación (2) en su forma log-aditiva:

log(Y_t) = log(T_t) × log(E_t) × log(I_t).          (3)

Asimismo, como comentamos en la introducción, en la literatura se han considerado otras opciones híbridas, por ejemplo, del tipo señalado por Ladiray y Quenneville (2000-2001):

Y_t = T_t × (1+E_t) × (1+I_t),          (4)

o del considerado por Findley et al. (1998):

  Y_t = T_t × (E_t + I_t – 1).          (5)

Podemos apreciar que, para el caso del modelo aditivo, suponen que la estacionalidad es estable e independiente de la componente de tendencia, mientras que en las opciones (2), (3) y (4), que la estacionalidad depende del nivel de la tendencia. Es esperable que el último patrón esté presente en una mayor cantidad de series de tiempo económicas.

En el entorno del X-13ARIMA-SEATS la expresión de la serie de tiempo puede ser generalizada como sigue:

 Y_{t =} μ_t + Z_t,       (6)

donde , es decir, son la suma de los efectos asociados a las K ≥ 1 variables explicativas, y sigue un modelo ARIMA multiplicativo estacional, donde B es el operador de retraso tal que BZ_t = Z_t-1;  ∇ = 1 – B;  es el operador de diferencia regular; ∇_s = 1–B^s es el operador de diferencia estacional, con periodo estacional s; ϕ(B) = 1 – ϕ₁ B –⋅⋅⋅– ϕ_p B^p es un polinomio autorregresivo regular de orden p; Φ(B) = 1 – Φ₁ B –⋅⋅⋅– Φ_p B^sP es un polinomio autorregresivo estacional de orden P; θ(B) = 1–θ₁ B–⋅⋅⋅–θ_q B^q es un polinomio de promedios móviles regular de orden q; Θ(B) = 1 – Θ₁ B–⋅⋅⋅–Θ_Q B^sQ es un polinomio de promedios móviles estacional de orden Q; α_t son variables aleatorias independientes y distribuidas de forma idéntica como una normal con media 0 y varianza σ² ; y d y D son los órdenes de diferencia regular y estacional, respectivamente. Los parámetros β_i, del modelo de regresión, así como los  ϕ,Φ,θ,Θ y σ² del modelo ARIMA son estimados de manera simultánea por el método de máxima verosimilitud.

De esta manera, si 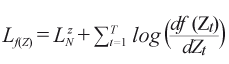 es el logaritmo de la función de verosimilitud, donde el primer término es maximizado para Z₁ , … , Z_t condicionado al pasado, es decir, a la parametrización del modelo ARIMA, y el segundo es la corrección por el tipo de transformación, es decir, si f(Z_t) = log Z_t, entonces este es ; el procedimiento del X-13ARIMA-SEATS para decidir si una serie de tiempo es aditiva o multiplicativa viene dado por L_Z > L_{log (Z)}, en el caso del modelo aditivo o bien L_Z < L_{log (Z)}, , en el del multiplicativo (ver Mood et al., 1974). De esta manera, L_{f (Z)} es invariante a la escala de la serie de tiempo.

De Guerrero et al. (2018) se concluye que, dados los supuestos del modelo, el cálculo de L_{f (Z)} está sujeto a suponer que tanto α_t  como  log (α_t) están distribuidas como una normal, lo cual resulta contradictorio dados los supuestos implícitos del modelo. En beneficio y en contra de este criterio, Findley et al. (1998, 37) comentan lo siguiente: “En el caso de elegir una transformación potencia en la serie de tiempo sin restricciones, cuando se usa el mismo tipo de modelo ARIMA y el mismo número de parámetros estimados, es conveniente centrarnos en el logaritmo de la función de verosimilitud que sea más grande. En esta situación, uno puede examinar un intervalo de valores para identificar la maximización del logaritmo de la función de verosimilitud, ver Ansley et al. (1977). Aunque este procedimiento parece arrojar resultados razonables (Shulman y McKenzie, 1984), la teoría de la distribución asintótica sobre la cual descansa no se ha verificado y, si es válido, puede requerir argumentos sutiles para su prueba cuando d > 0 o D > 0 …”.

Por otra parte, la trasformación Box y Cox (1964) es una técnica de transformación potencia para reducir anomalías en las series de tiempo, como no aditividad (no linealidad), no normalidad y heterocedasticidad. Definimos y^λ  = (y^λ  – 1)/ λ si λ  ≠ 0 y y^λ = log(y) si  λ = 0, lo cual puede ser usado como una aproximación para estabilizar la varianza.

Guerrero (1993) deduce que para una variable aleatoria X > 0 , donde E (X) =μ_{x <} ∞  y var (X)  depende de la media, la transformación estabilizadora de la varianza satisface que para una λ :

               

para una constante α > 0 , es decir, λ es tal que el coeficiente de variación es una constante positiva. En la práctica se utilizan los respectivos estimadores de la varianza y la media, en consecuencia, podemos estimar (para submuestras h = 1, … , H) el coeficiente de variación muestral como , donde:

con Z_hr siendo la r-ésima observación de la subserie h cuya dimensión es R. Es claro observar que nos interesa encontrar el parámetro λ, donde el coeficiente de variación muestral es estadísticamente constante para una serie de submuestras H. Existen otras estrategias para seleccionar λ, las cuales son detalladas en Guerrero (1993), pero la esencia es similar al enfoque comentado con anterioridad.

Análisis empírico

Análisis de desestacionalización

Para desestacionalizar de forma individual las series de tiempo del ITAEE, se comparan tres modelos: 1) los automáticos que arroja el X-13ARIMA-SEATS, 2) los publicados por el INEGI de manera oficial y 3) una variante, que tiene como motor la transformación potencia de Guerrero (1993) que, posteriormente, busca el modelo que mejor satisfaga los supuestos que validan el correcto ajuste estacional dentro de un amplio conjunto de modelos ARIMA definidos de forma previa. Lo anterior se realiza para el periodo de 2003-T1 a 2019-T2, dado que es para esta longitud en la que se pueden utilizar los modelos del Instituto I para poder replicar los resultados oficiales. No se considera el periodo de 1980-T1 a 2002-T4, que es donde el INEGI retropoló las series de tiempo a través de modelos econométricos y estadísticos y en el cual se utilizan otros modelos que no son publicados oficialmente en la actualidad (INEGI 2019, 4). No omitimos señalar que los modelos del Instituto no utilizan de forma directa los resultados generados de manera automática por el X-13ARIMA-SEATS, sino que se especifican y estiman de acuerdo con los pasos que fueron comentados en la introducción, situación que los modelos automáticos no contemplan en su totalidad debido a la búsqueda sistemática y heurística de los modelos ARIMA.

La transformación potencia de las series de tiempo a través de la metodología de Guerrero (1993) se realiza restringiendo la búsqueda de parámetros λ entre 0 y 1 y redondeando el caso decimal para fijar entre la selección de modelos aditivos (λ = 0 ) y multiplicativos ( λ = 1 ).

Para comparar estadísticamente los tres enfoques, se analizan las siguientes pruebas:

• Estadístico QS de estacionalidad: p valores de la prueba que indica bajo hipótesis nula que no hay evidencia de estacionalidad residual.
• Estadístico de Friedman de estacionalidad: p valores de la prueba que indica bajo hipótesis nula que no hay evidencia de estacionalidad residual.
• Estadístico Ljung-Box: p valores de la prueba que indica bajo hipótesis nula que no hay evidencia de autocorrelación serial en los errores del modelo ARIMA.
• Estadístico Shapiro-Wilk: p valores de la prueba que indica bajo hipótesis nula que los residuales se distribuyen normal.
• Criterio de AIC: estadístico que indica el tamaño de la varianza residual penalizado por el número de parámetros del modelo subyacente.
• Tipo de transformación potencia sugerida: ninguna (serie aditiva) o logarítmica (serie multiplicativa).

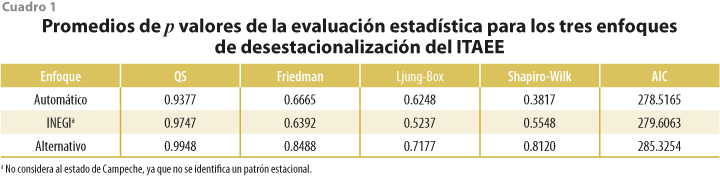
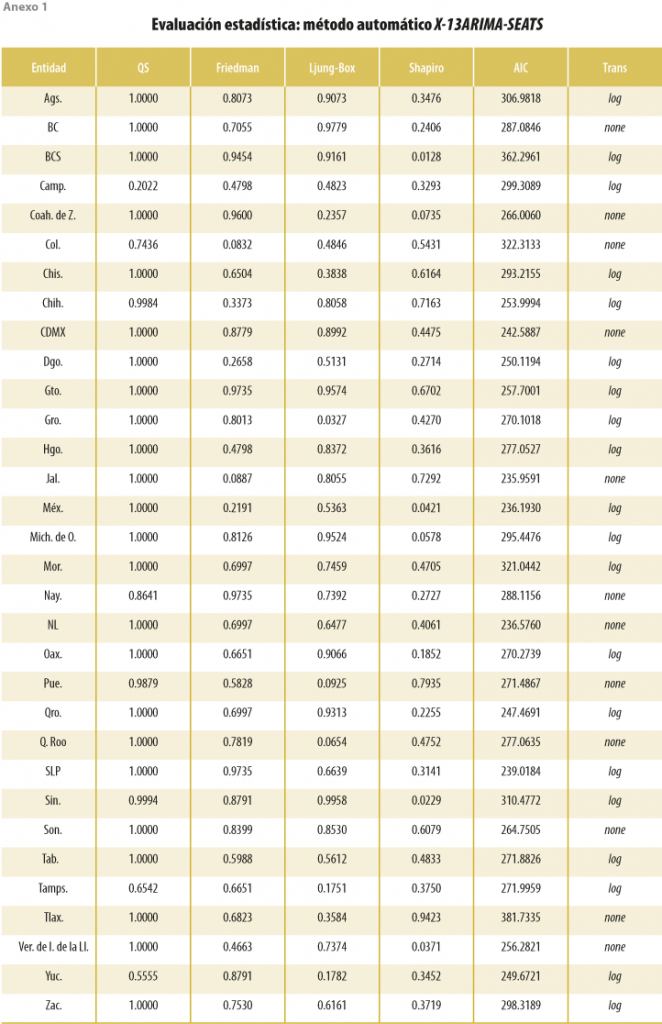
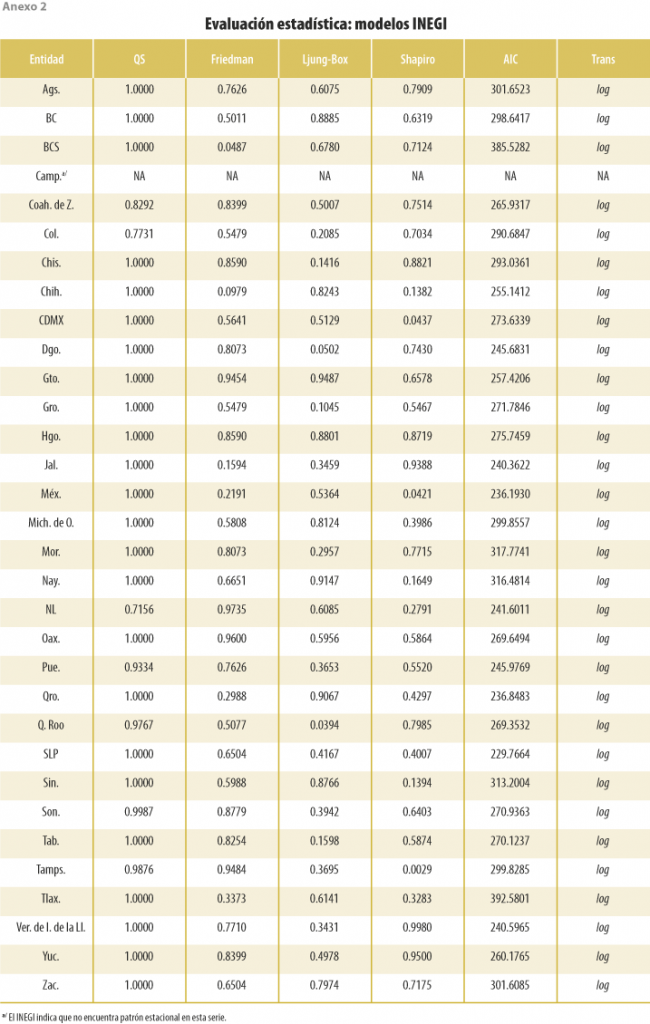
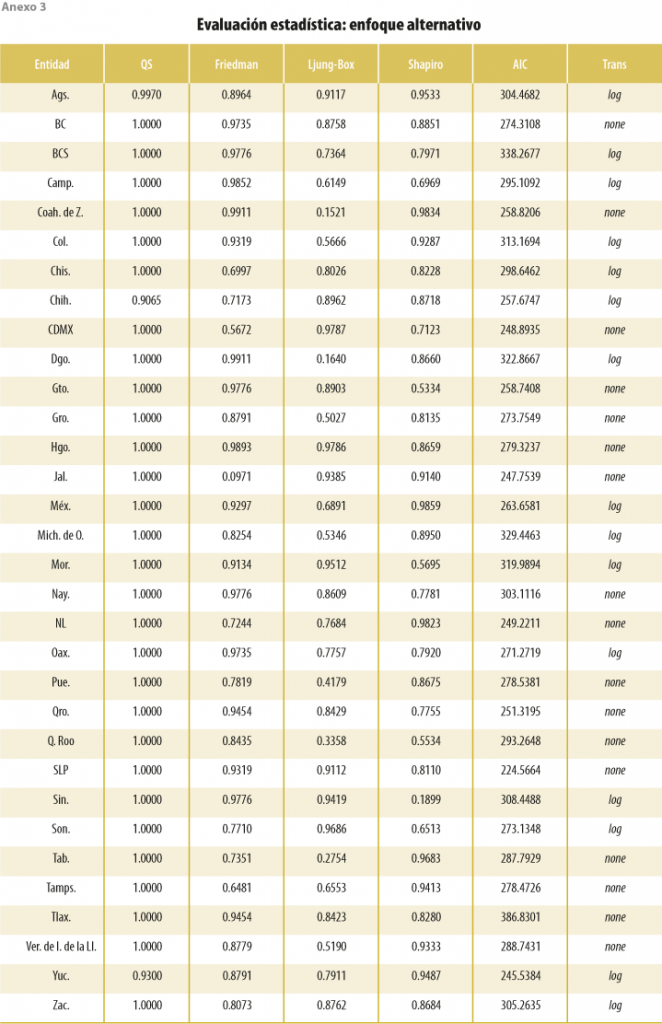
Los resultados para los estadísticos QS, Friedman, Ljung-Box, Shapiro-Wilk y AIC se resumen en el cuadro 1, mientras que en los anexos se muestran con detalle los de cada entidad federativa y enfoque.

Se puede apreciar que, en términos generales, los tres enfoques tienen buenas propiedades estadísticas, considerando como buenos modelos aquellos libres de estacionalidad (QS y Friedman) y autocorrelación residual (Ljung-Box) y donde los residuales se distribuyen normalmente (Shapiro-Wilk). No obstante, se puede apreciar que, en términos absolutos, el enfoque alternativo, que considera la transformación potencia con el enfoque de Guerrero (1993), otorga p valores más cercanos a 1 en las cuatro pruebas, lo que nos indica evidencia más fuerte de ausencia de estacionalidad y autocorrelación serial, además de que los residuales siguen de mejor manera una campana gaussiana. También, es claro que el enfoque automático es el que otorga mejores AIC dado que es su objetivo. Por último, es interesante comentar, además, que el enfoque automático parece ser ligeramente mejor que el modelo INEGI, con excepción del estadístico QS. Una razón puede deberse a que los del Instituto se actualizan con cierta periodicidad, lo cual, como corolario, daría indicios de que requieren ponerse al día con mayor frecuencia.

Al evaluar caso por caso (ver anexos), los resultados indican que el modelo automático detecta que en 20 entidades federativas la transformación potencia óptima es la logarítmica, el enfoque alternativo determina 15 casos, mientras que el del INEGI afirma que, en las 31 ocasiones, el mejor modelo es el multiplicativo (transformación logarítmica).^[1] Por otra parte, a un nivel de significancia de 5 %, el enfoque automático rechaza en una ocasión la hipótesis nula de autocorrelación y cuatro veces la prueba de normalidad, mientras que la modelación del Instituto lo hace en una y tres, respectivamente, aunque también en una se rechaza la hipótesis nula según el estadístico de Friedman. Por otra parte, en el enfoque alternativo, en ninguna ocasión se rechaza la hipótesis nula para cualquier prueba. Los resultados se mantienen para los subperiodos 2003-T1 a 2010-T2, 2003-T1 a 2013-T2 y 2003-T1 a 2016-T2, los cuales están disponibles bajo petición.^[2]

En conclusión, de acuerdo con los criterios tradicionales para medir la calidad en el proceso de desestacionalización, el enfoque alternativo proporciona mejores resultados para las series del ITAEE.^[3]

Modelo de factores

El análisis de factores tiene como objetivo resumir el comportamiento de N series de tiempo en un r < N factores comunes, más componentes individuales, llamadas términos idiosincráticos. En este contexto, partimos de la siguiente representación:

X_t = ΨF_t + ε_t,                                        (9)

  F_t = AF_t-1 + n_t                                       (10)

 ε_t = Γε_t-1 + u_t,                                        (11)

donde las observaciones (X_t), el error idiosincrático (ε_t) y su error asociado (u_t) son de dimensión N × 1. Por otra parte, los factores comunes (F_t) y su término de error (n_t)  son de tamaño r × 1, mientras que la contribución de los factores sobre las observaciones (Ψ) es una matriz N × r. Para finalizar, A y Γ son las matrices de coeficientes de modelos de vectores autorregresivos de dimensión r × r y N × N, respectivamente. Se supone que los factores y el error idiosincrático pueden ser I(1).

Nótese que el número de factores r es desconocido, por lo tanto, recurrimos al método de Onatski (2010) para estimarlo. Se utiliza este procedimiento debido a que Corona et al. (2017) prueban que, en muestras finitas, dicha metodología funciona aun cuando el término idiosincrático es I(1) para distintos procesos generadores de datos.

Por otra parte, la estimación de los factores se realiza siguiendo el procedimiento de Barigozzi et al. (2017), de tal forma que el estimador de Ψ viene dado por los r valores propios de la matriz de ΔXΔX’, donde X es de dimensión N × T. Por lo tanto, puede mostrarse que el estimador de F_t viene dado por la siguiente expresión:

Usando el procedimiento de Onatski (2010) para los datos oficialmente desestacionalizados y los que otorgan los modelos automáticos, encontramos que , mientras que para el enfoque alternativo se determina que . La implicación econométrica más importante es que este último enfoque indica que se requiere de un factor más respecto a los otros con el fin de poder representar la variabilidad total de los ITAEE para las 32 entidades.

Es importante señalar que, econométricamente, si al menos un factor es I(1) y, además, podemos concluir que el error idiosincrático es I(0), implicaría que existe al menos un par de economías estatales cointegradas (Bai, 2004). Nótese que en este caso, cuando los factores son I(1) y el término idiosincrático es I(0), los factores comunes son ahora las tendencias comunes.

Para verificar la naturaleza estocástica de los factores y el error idiosincrático, se estima el ejercicio PANIC (Bai y Ng, 2004) para determinar cuántos factores son I(1) y si el error idiosincrático es I(0). Los resultados indican que, para los tres conjuntos de datos, los factores comunes son I(1), mientras que los errores idiosincráticos son I(0).

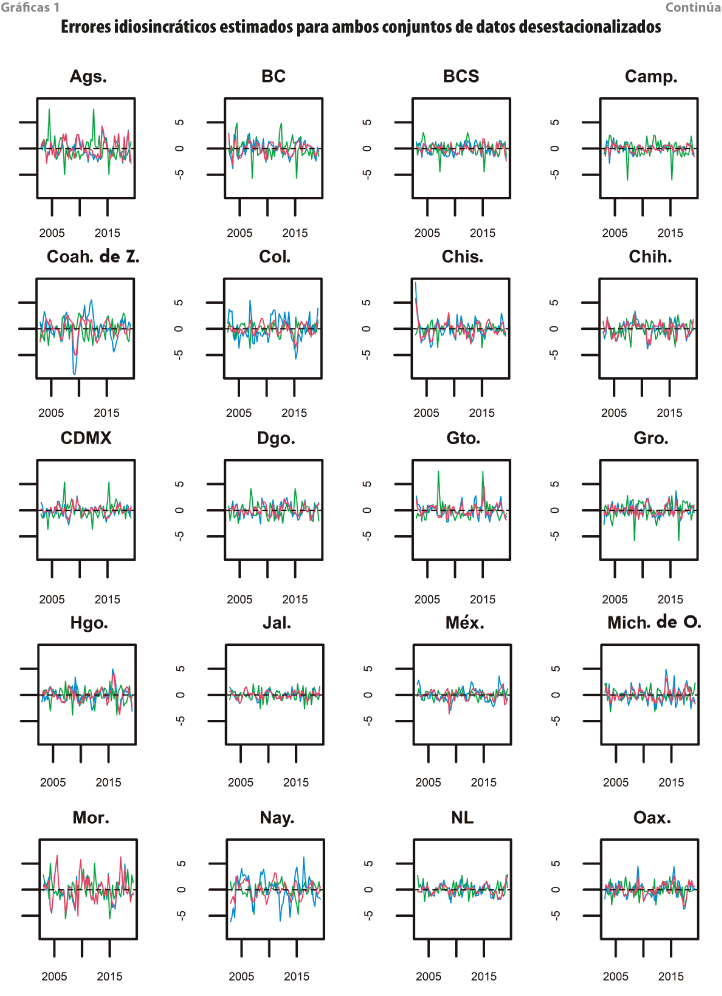
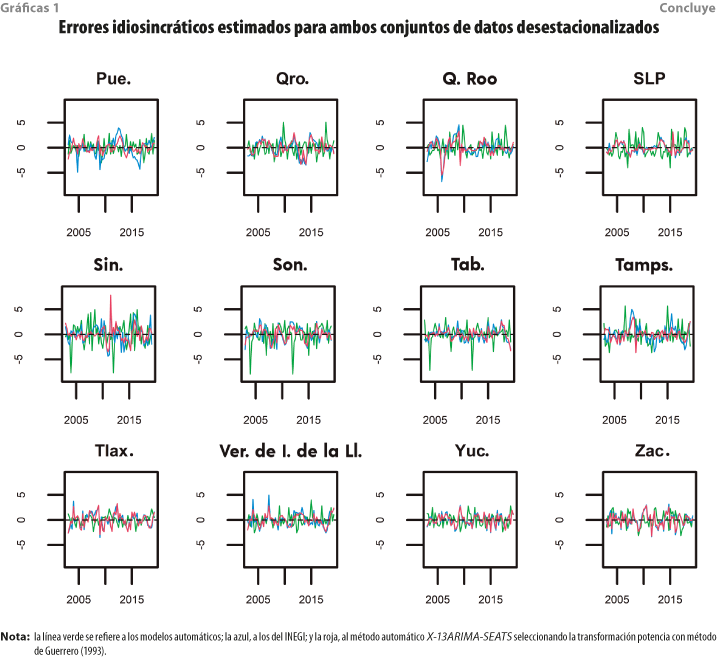
El conjunto de gráficas 1 muestra el comportamiento de los términos idiosincráticos. Econométricamente, estos representan la desviación respecto a la tendencia común; de esta forma, pueden interpretarse como la componente a corto plazo de cada una de las economías.

+

Se puede apreciar que los comportamientos a corto plazo de las economías cuando utilizamos modelos automáticos son muy volátiles, lo que da indicios de ciertos problemas en poder captar la variabilidad residual a través de los factores estimados. Por otra parte, para el conjunto de datos desestacionalizados con los modelos del INEGI y para la metodología alternativa sugerida en este trabajo, las series son similares, aunque destaca que, para Coahuila de Zaragoza, Colima y Nayarit, los movimientos de los comportamientos idiosincráticos presentan una mayor variabilidad, hecho atribuible, posiblemente, a la existencia de un factor común más para explicar la variabilidad en la economía. En consecuencia, el nivel mínimo de los términos idiosincráticos cuando usamos cifras desestacionalizadas con los modelos del INEGI es -8.8, mientras que el enfoque alternativo nos ofrece que es -5.5. Por otra parte, el nivel máximo se alcanza en 8.9 cuando se usan los modelos del Instituto y 7.8 para el otro procedimiento.

Como los factores comunes son sensibles a la estimación, es decir, a las condiciones de identificabilidad para poder ser estimados, nos centramos en el comportamiento del primer factor, el cual es invariante a la posible rotación utilizada, a la par de que, por construcción, es el que aporta mayor porcentaje de explicación respecto a la variabilidad total observada.

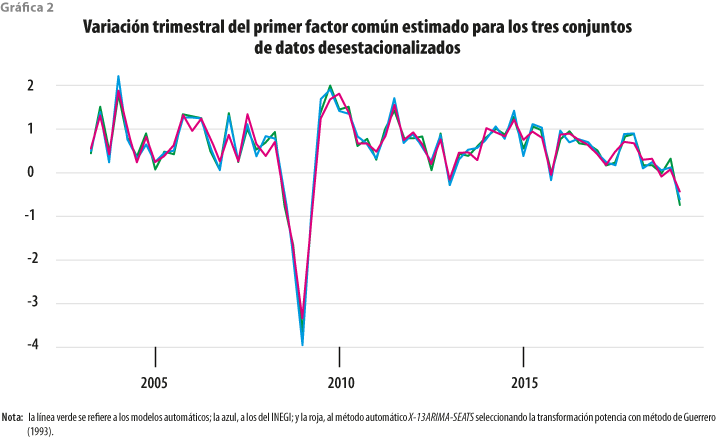
La gráfica 2 muestra el comportamiento de la variación trimestral del primer factor común estimado para los tres conjuntos de datos.

Se puede apreciar que los factores comunes presentan variaciones muy similares, donde llama la atención la caída asociada al último periodo, la cual es menor cuando se estiman aquellos con las series desestacionalizadas usando los modelos del INEGI. Utilizando estos y al centrar la atención en los últimos cuatro trimestres, las variaciones trimestrales indican crecimientos de 0.3, 0.1, 0.1 y -0.6 %, mientras que si empleamos el enfoque alternativo, obtenemos variaciones de 0.3, -0.1, 0.1 y -0.4 %, lo cual, aunque de manera estadística puede resultar igual, no necesariamente lo es en términos económicos, sobre todo cuando las tasas de crecimiento son cercanas a 0 por ciento. Los modelos automáticos otorgan fluctuaciones más cercanas a las cifras oficiales, es decir, 0.2, 0.0, 0.3 y -0.7 por ciento.

En resumen, el análisis de factores utilizado en este trabajo nos muestra que, cuando usamos el enfoque alternativo, encontramos que existe un factor más que explica la variabilidad de las series que si empleamos el automático o los modelos del INEGI. Esto, en sí, no es una razón en favor o en contra de utilizar alguno de los procedimientos, sino que indica que las estimaciones pueden ser sensibles al conjunto de datos con los cuales se realiza el análisis de factores. Lo que sí señala es que hay mayor variabilidad en el conjunto de datos desestacionalizados con el enfoque alternativo, por lo cual requerimos un factor más que, en términos econométricos, representa estimar términos idiosincráticos con menor volatilidad. Por otra parte, la primera tendencia común de la economía muestra ligeramente tasas de crecimiento menores en el último periodo de la serie cuando se utilizan los modelos del INEGI o los automáticos para desestacionalizar las series de tiempo, que cuando se utiliza el enfoque alternativo.

 

Conclusiones

La contribución de este trabajo es mostrar un análisis que mida los efectos de la transformación potencia en el proceso de desestacionalización bajo el contexto del X-13ARIMA-SEATS.

Se evaluó el funcionamiento de su método automático, los modelos que proporciona el INEGI y una alternativa que se basa en elegir la transformación potencia con el método de Guerrero (1993); lo anterior, para las series del ITAEE. Los resultados obtenidos permiten concluir que el enfoque alternativo otorga mejores resultados, en el sentido de que hay evidencia más fuerte de ausencia de estacionalidad y autocorrelación serial en las series desestacionalizadas. Además, dada la importancia que tiene el proceso de desestacionalización para hacer análisis de coyuntura económica, el estudio de factores indicó que desestacionalizar de mejor forma las series de tiempo (es decir, mediante nuestra propuesta), nos otorga errores idiosincráticos menos volátiles, lo que genera ciertas discrepancias en las variaciones trimestrales de los factores comunes; en otras palabras, resultados econométricos más robustos.

Esta investigación permitió corroborar que el método de Guerrero (1993) es una herramienta valiosa para discernir entre realizar el ajuste estacional con una descomposición aditiva o bien multiplicativa. No obstante, en este caso solo se presentó para una variable, por lo que limita poder extender estas conclusiones a otras series económicas relevantes, como el PIB, el IGAE y el consumo privado, entre otras. Por ello, se recomienda, como líneas futuras de investigación, realizar un experimento más robusto para series de tiempo estacionales simuladas, que permita evaluar el funcionamiento de la técnica propuesta abarcando una amplia gama de escenarios y no solo en una aplicación empírica.

Fuentes

Ansley, C. F., W. A. Spivey y W. J. Wrobleski. “A class of transformations for Box‐Jenkins seasonal models”, en: Journal of the Royal Statistical Society: Series C (Applied Statistics). 26(2). 1977, pp. 173-178.

Bai, Jushan y Serena Ng. “A PANIC attack on unit roots and cointegration”, en: Econometrica. 72, núm. 4. 2004, pp. 1127-1177.

Bai, Jushan. “Estimating cross-section common stochastic trends in nonstationary panel data”, en: Journal of Econometrics. 122, núm. 1. 2004, pp. 137-183.

Barigozzi, Matteo, Marco Lippi y Mateo Luciani. Dynamic factor models, cointegration, and error correction mechanisms. Working paper. 2017. arXiv:1510.02399v3.

Box, George. E. y David R. Cox. “An analysis of transformations”, en: Journal of the Royal Statistical Society: Series B (Methodological). 6(2). 1964, pp. 211-243.

Corona, Francisco, Pilar Poncela y Esther Ruiz. “Estimating non-stationary common factors: implications for risk sharing”, en: Computational Economics. 2017, pp. 1-24.

Dagum, Estela Bee. The X-11 ARIMA Seasonal Adjustment Method. Catalogue 12-564E. Ottawa, Canada, Statistics Canada, 1980.

Findley, David F., Brian C. Monsell, William R. Bell, Mark C. Otto y Bor-Chung Chen. “New capabilities and methods of the X-12-ARIMA seasonal-adjustment program”, en: Journal of Business & Economic Statistics. 16(2). 1998, pp. 127-152.

Guerrero, Victor M. “Time series analysis supported by power transformations”, en: Journal of Forecasting. 12(1). 1993, pp. 37-48.

Guerrero, Víctor M., Jesús López-Pérez y Francisco Corona. “Ajuste estacional de series de tiempo económicas en México”, en: Realidad, Datos y Espacio Revista Internacional de Estadística y Geografía. 9(3). 2018, pp. 74-97.

INEGI. Indicador Trimestral de la Actividad Económica Estatal. Producto Interno Bruto trimestral, anual y anual por entidad federativa. Retropolación hasta 1980. Síntesis metodológica. Aguascalientes, INEGI, 2019.

Ladiray, Dominique y Benoit Quenneville. “Desestacionalizar con el método X-11”, en: Methodologica. 8-9. Bruxelles, Belgique, Universite Libre de Bruxelles, 2000-2001.

Mood, Alexander M., Franklin A. Graybill y Duane C. Boes. Introduction to the theory of statistics. McGraw-Hill, 1974.

Onatski, Alexei. “Determining the number of factors from empirical distribution of eigenvalues”, en: The Review of Economics and Statistics. 92(4). 2010, pp. 1004-1016.

Shulman, Holly B. y Sandra K. McKenzie. A Study of Pre-Adjustment Transformations. Bureau of the Census. 1984.

 

 

Anexos

 

^[1] Para Campeche, el INEGI no ajusta un modelo estacional.

^[2] Agradecemos el comentario de un árbitro anónimo que motivó realizar este ejercicio.

^[3] En un ejercicio adicional, se estimó esta parte para las series del Indicador Global de la Actividad Económica (IGAE) del INEGI y sus componentes, las cuales arrojaron evidencia en favor del método propuesto. Dichos resultados están disponibles bajo petición a los autores.